高一数学竞赛综合练习题(无答案)

高一数学竞赛综合练习题
选择题：
1、设集合，则是（ ）
A、S B、T C、 D、有限集
2、函数是奇函数，则一定有（　　）
A、　　　　　　B、　　　　　C、　　　　　　D、
3、关于函数 下列判断正确的是（ ）
A、是增函数 B、是减函数 C、是奇函数 D、是偶函数
4、若则实数a的取值范围是 （ ）
A、 B、 C、 D、或
5、函数①,②,③,④在单调递减的个数是 （ ）
A、1 B、2 C、3 D、4
6、设则 （ ）
A、0 < a < b < 1 B、0 < b < a <1 C、a >b >1 D、b>a>1
7、函数的图像如图所示，则 （ ）
A、a > 0 , b > 0 , c > 0 B、a > 0 , b > 0 , c < 0
C、a < 0 , b < 0 , c > 0 D、a < 0 , b < 0 , c < 0
8、下列函数可用二分法确定出零点的是 （ ）
A、 B、
C、 D、
9、函数有零点的区间是 （ ）
A、（- 1，0） B、（2 ， 3） C、（1，2） D、（0，1）
10、拟定从甲地到乙地通话m分钟的电话费由给出，其中m > 0,[m]是大于或等于m的最小整数（如[3]=3, [3.7]=4, [3.1]=4）,则从甲地到乙地通话时间为5.5分钟的电话费为 （ ）
A、3.71 B、3.97 C、4.24 D、4.77
11、若的最小正周期是2T，且有对一切实数x恒成立，则是 （ ）
A、奇函数 B、偶函数 C、既是奇函数又是偶函数 D、既不是奇函数又不是偶函数
12、设是上的奇函数，，当时，，则等于 （ ）
A、- 0.5 B、0.5 C、1.5 D、- 1.5
13、已知在[0 , 1]上是x的减函数，则a的取值范围是 （ ）
A、（0，1） B、（1，2） C、（0，2） D、
14、已知是定义在R上的偶函数，在上为增函数，且，则不等式的解为 （ ）
A、 B、 C、 D、
15、下列四个结论①偶函数的图像一定与y轴相交，②奇函数的图像一定通过原点，③偶函数的图像关于y轴对称，④既是奇函数又是偶函数的函数一定是。其中正确命题的个数是 （ ）
A、1个 B、2个 C、3个 D、4个
16、对于，下列各结论中，正确的是 （）
①若M = N，则 ②若，则M = N ③若，则M = N ④若M = N，则
A、①③ B、②④ C、② D、①②③④
17、已知函数是偶函数，在[0，2]上是单调减函数，则（ ）
A、 B、
C、 D、
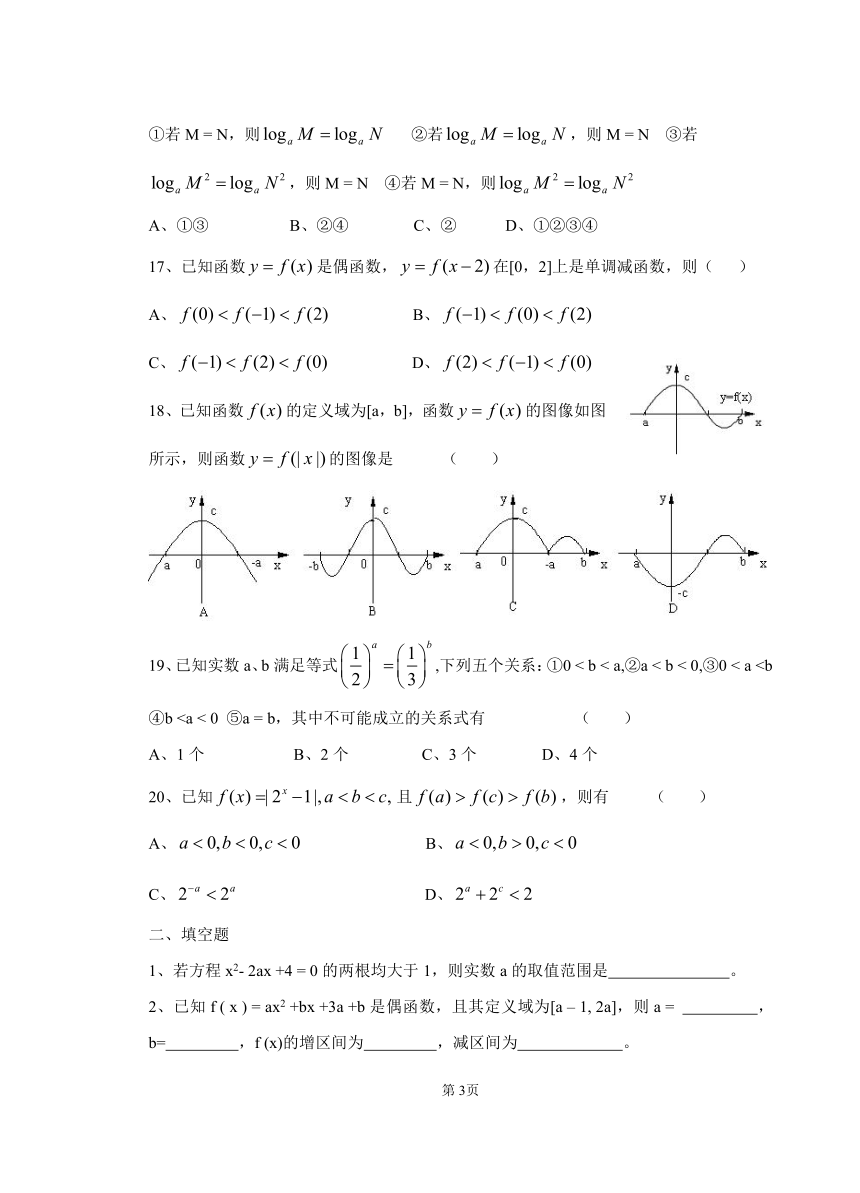
18、已知函数的定义域为[a，b]，函数的图像如图所示，则函数的图像是 （ ）
19、已知实数a、b满足等式,下列五个关系：①0 < b < a,②a < b < 0,③0 < a A、1个 B、2个 C、3个 D、4个
20、已知且，则有 （ ）
A、 B、
C、 D、
填空题
1、若方程x2- 2ax +4 = 0的两根均大于1，则实数a的取值范围是 。
2、已知f ( x ) = ax2 +bx +3a +b是偶函数，且其定义域为[a – 1, 2a]，则a = ，b= ，f (x)的增区间为 ，减区间为 。
3、将二次函数y = -2x2的图像的顶点移到（-3，2）后，得到的函数图像对应的解析式为 。
4、函数y = 3x-3+4恒过定点 。
5、已知f (x) =(x -a) (x -b) – 2,（a < b）, m，n（m6、若函数是奇函数，则a = 。
7、f(x) = x2+2ax +a2 +b,当f(x)在区间上为减函数时，a的取值范围是 ，若x∈R,恒有f(x)≥0,则b的取值范围是 ，若f(x)为偶函数，则有 。
8、对于函数f(x)定义域中任意的x1，x2 （x1≠x2），有如下结论：①,②,③,④,当时，上述结论中正确的序号是 。
9、函数f (x) = 3ax +1 –2a在（-1，1）内有零点，则a的取值范围是 。
10、函数f (x) = | x2 – 4x +3 |的递增区间为 ，递减区间为 。若方程| x2 – 4x +3 | = a有四个不相等的实数根，则实数a的取值范围是 。
11、当2 < x < 4时，2x，x2，log2x的大小关系是 。
12、将进货单价为80元的商品按90元一个出售时，能卖出400个，根据经验，该商品若每个涨（降）1元，其销售量就减少（增加）20个，为获得最大利润，售价应定为 元。
解答题
1、设A = {x| |x+1|(2)AB=
2、计算下列各式的值
1)
2)
3)
3、函数f(x) = x2 – bx +c满足f(1+x) = f(1- x)且f(0) =3,比较f(bx)与f(cx)的大小。
4、已知函数，（1）求函数f(x)的定义域，值域。
（2）判断f(x)的单调性，并证明。
5、某商品在近30天内每件的销售价格P元与时间t （天）的函数关系是
,该商品的日销量Q（件）与时间t（天）的函数关系是Q = - t + 40,(06、已知函数在[0,1]上的最大值为2，求实数a的值。
7、对于函数f(x),若存在x0∈R,使f(x0) = x0成立，则称x0为f(x)的不动点。
已知f(x)=ax2+(b+1)x+(b+1), (a ≠0).
当a = 1，b = - 2时，求f(x)的不动点。
（2）若对任意实数b，函数f(x)恒有两个相异的不动点，求a的取值范围。