一元二次方程--配方法

课件13张PPT。用配方法---
解一元二次方程学习目标1、理解掌握一元二次方程的四种解法；
2、了解什么是配方法？
3、会用配方法解一元二次方程。自学指导1、阅读：P35——P362、思考：
（1）了解什么是配方法？
（2）会用配方法解一元二次方程。 一般地,对于形如x2=a(a≥0)的方程,
根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法.例1.用开平方法解下列方程:
(1)3x2－27=0;
(2)(2x－3)2=7
巩固练习 1（１）方程　　　　的根是
（２）方程　　　　　的根是　　
（3） 方程 　　　　的根是 2. 选择适当的方法解下列方程：
（1）x2－ 81＝0 （2） x2 ＝50
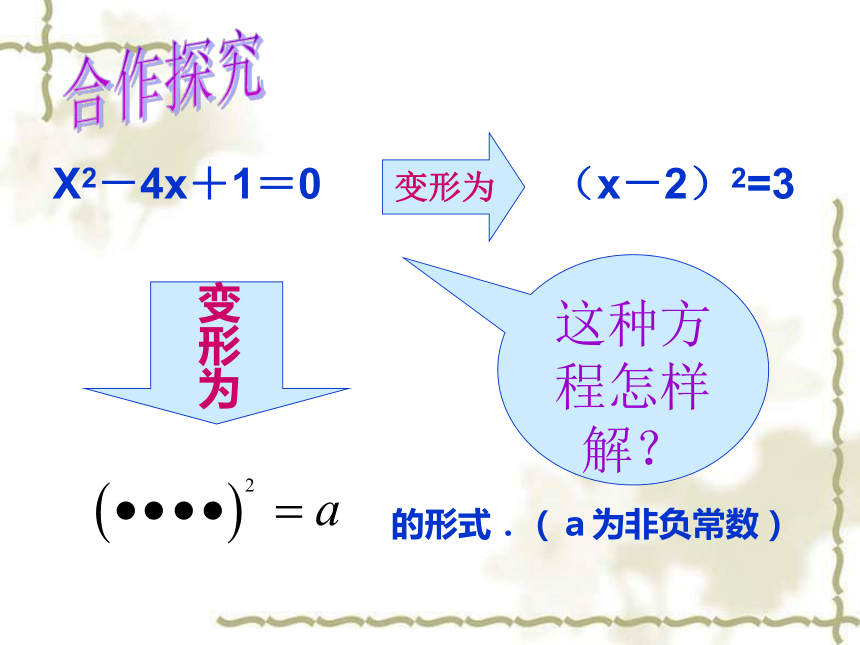
(3)(x＋1)2=4 (4)x2＋2 x＋5=0X1=0.5, x2=－0.5X1＝3， x2＝—3X1＝2， x2＝－1合作探究这种方程怎样解？变形为的形式．（ａ为非负常数）变形为X2－4x＋1＝0（x－2）2=3 把一元二次方程的左边配成一个完全平方式,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.(1)x2＋8x＋ =(x＋4)2
(2)x2－4x＋ =(x－ )2
(3)x2－___x＋ 9 =(x－ )2填空 配方时, 等式两边同时加上的是一次项系数一半的平方166342例2：用配方法解下列方程
(1)x2＋6x=1
(2)x2=6－5x
用配方法解一元二次方程的步骤:移项:把常数项移到方程的右边;
配方:方程两边都加上一次项系数一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
定解:写出原方程的解.(2) －x2＋4x－3=0(1) x2＋12x =－9做一做练习3：用配方法解下列方程： 4. 用配方法说明：不论k取何实数，多项式
k2－3k＋5的值必定大于零.思考：先用配方法解下列方程：
（1） x2－2x－1＝0 （2） x2－2x＋4＝0
（3） x2－2x＋1＝0
然后回答下列问题：
（1）你在求解过程中遇到什么问题？你是怎样处理所遇到的问题的？
（2）对于形如x2＋px＋q＝0这样的方程，在什么条件下才有实数根？谈谈你的收获！！ 1.一般地,对于形如x2=a(a≥0)的方程,
根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法. 2.把一元二次方程的左边配成一个完全平方式,然后用开平方法求解,这种解一元二次方程的方法叫做配方法. 注意:配方时, 等式两边同时加上的是一次项
系数一半的平方.用配方法解一元二次方程的步骤:移项:把常数项移到方程的右边;
配方:方程两边都加上一次项系数一半的平方;
开方:根据平方根意义,方程两边开平方;
求解:解一元一次方程;
定解:写出原方程的解.