对数的基本概念(1)(台州教学大比武)
文档属性
| 名称 | 对数的基本概念(1)(台州教学大比武) |  | |
| 格式 | rar | ||
| 文件大小 | 885.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-25 23:19:00 | ||
图片预览





文档简介
课件17张PPT。对数的概念(一) “给我空间、时间、及对数,我就可以创造一个宇宙”
——伽利略 恩格斯把对数的发明、解析几何的创始、
微积分的建立并称为17世纪数学的三大成就。 法国著名的数学家、天文学家拉普拉斯曾说:
“对数,可以缩短计算时间,在实效上等于把天文
学家的寿命延长了许多倍”。 提出问题1.庄子:一尺之棰,日取其半,万世不竭。2.假设2004年我国国民生产总值为a亿元,
如果每年平均增长8%,1)2008年我国国民生产总值是多少?2)经过多少年国民生产总值比2004年翻一翻?2)取多少次,还有0.125尺长?1)取4次,还有多长?抽象出:1 这是一个已知底数和幂的值,求指数的问题。有三个数1.08(底),x(指数)和2(幂)温故而知新(1)由1.08,x得到数2的运算是(2)由x,2得到数1.08的运算是(3)由1.08,2得到数x的运算是乘方运算。开方运算。对数运算 对于上述问题,苏格兰数学家纳皮尔创造了一种被人们广泛接受的表示方法X=log1.082 这里我们只从形式上解出了x,但x到底等于
多少我们还不知道?
即1.08x=2X=log1.082log是拉丁文logarithm(对数)的缩写 为了知道x到底等于多少,我们先来研究
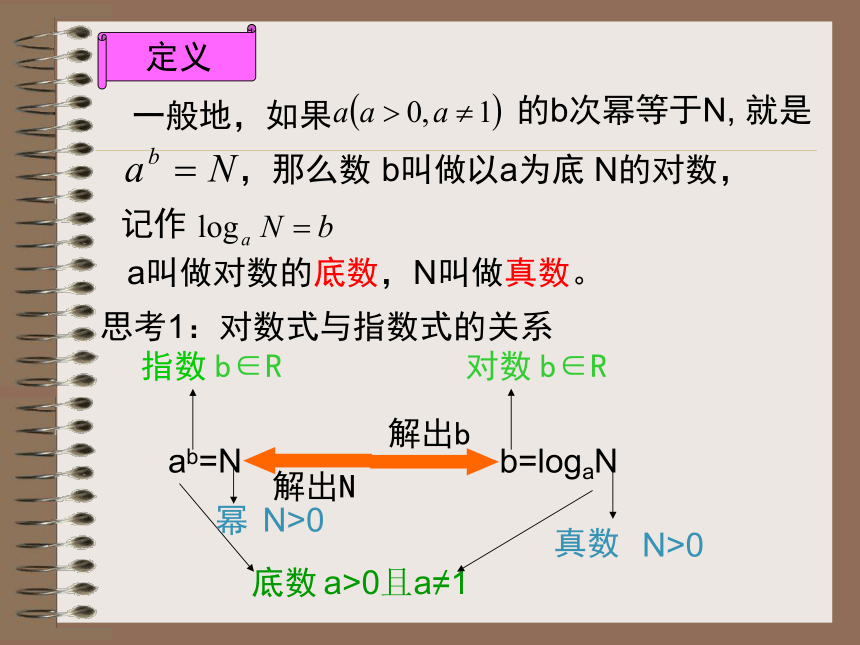
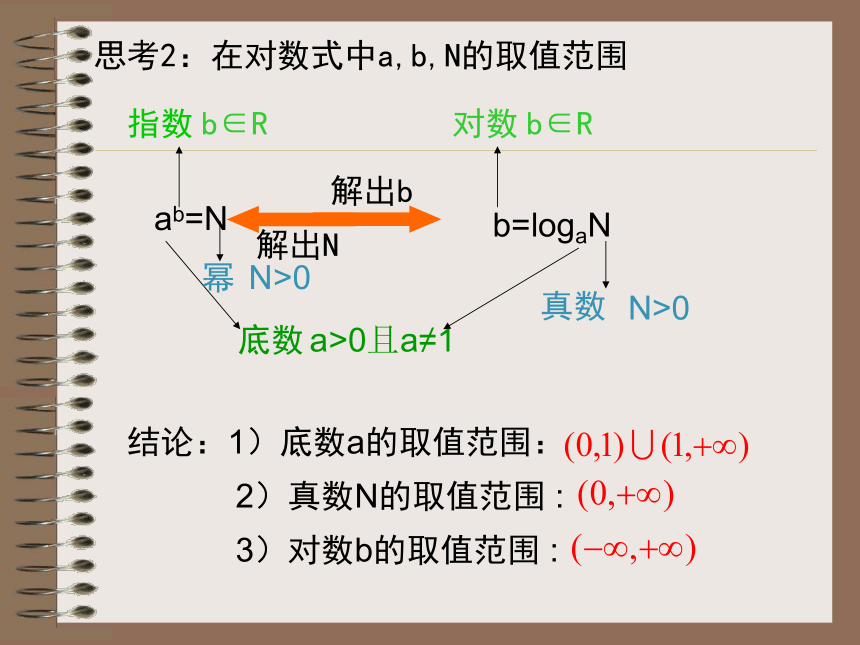
对数的有关概念读作“x等于以1.08为底2的对数”a叫做对数的底数,N叫做真数。定义ab=Nb=logaN思考1:对数式与指数式的关系结论:1)底数a的取值范围: 2)真数N的取值范围 :思考2:在对数式中a,b,N的取值范围3)对数b的取值范围 :举例应用例题1,把下列各式对数式化为指数式,
指数式化为对数式。1)常用对数: 我们通常将以10为底的对数叫做常用对数。 简记作lg5; 2)自然对数: 在科学技术中常常使用以无理数e=2.71828……为底的对数,以e为底的对数叫自然对数。 为了简便,N的自然对数 简记作lnN。 简记作ln3 ; 简记作ln10基本概念为了简便,N的常用对数 简记作lgN。 简记作lg3.5. 课堂练习:阅读教材P75----P76
然后完成书P76 练习 :1, 2 例题2,计算下列各式。 则 解:设 解:设 则 思考3:loga1=? logaa=? 01练习,计算下列各式。=1=01.知识点小结:
本节课学习了对数的概念以
及指数式与对数式互相转化课堂小结:2.思想方法小结:
逆向思维
用联系的观点看问题
布置作业1)阅读教材P80的阅读材料,进一步了解对数
的发明过程。2)书P79 习题2.7 1 2
课外思考题再见谢谢各位专家指导 对数的创始人是苏格兰数学家纳皮尔(Napier,1550年~1617年)。在纳皮尔所处的年代,哥白尼的“太阳中心说”刚刚开始流行,这导致天文学成为当时的热门学科。可是由于当时常量数学的局限性,天文学家们不得不花费很大的精力去计算那些繁杂的“天文数字”,因此浪费了若干年甚至毕生的宝贵时间。纳皮尔也是当时的一位天文爱好者,为了简化计算,他多年潜心研究大数字的计算技术,终于独立发明了对数。
——伽利略 恩格斯把对数的发明、解析几何的创始、
微积分的建立并称为17世纪数学的三大成就。 法国著名的数学家、天文学家拉普拉斯曾说:
“对数,可以缩短计算时间,在实效上等于把天文
学家的寿命延长了许多倍”。 提出问题1.庄子:一尺之棰,日取其半,万世不竭。2.假设2004年我国国民生产总值为a亿元,
如果每年平均增长8%,1)2008年我国国民生产总值是多少?2)经过多少年国民生产总值比2004年翻一翻?2)取多少次,还有0.125尺长?1)取4次,还有多长?抽象出:1 这是一个已知底数和幂的值,求指数的问题。有三个数1.08(底),x(指数)和2(幂)温故而知新(1)由1.08,x得到数2的运算是(2)由x,2得到数1.08的运算是(3)由1.08,2得到数x的运算是乘方运算。开方运算。对数运算 对于上述问题,苏格兰数学家纳皮尔创造了一种被人们广泛接受的表示方法X=log1.082 这里我们只从形式上解出了x,但x到底等于
多少我们还不知道?
即1.08x=2X=log1.082log是拉丁文logarithm(对数)的缩写 为了知道x到底等于多少,我们先来研究
对数的有关概念读作“x等于以1.08为底2的对数”a叫做对数的底数,N叫做真数。定义ab=Nb=logaN思考1:对数式与指数式的关系结论:1)底数a的取值范围: 2)真数N的取值范围 :思考2:在对数式中a,b,N的取值范围3)对数b的取值范围 :举例应用例题1,把下列各式对数式化为指数式,
指数式化为对数式。1)常用对数: 我们通常将以10为底的对数叫做常用对数。 简记作lg5; 2)自然对数: 在科学技术中常常使用以无理数e=2.71828……为底的对数,以e为底的对数叫自然对数。 为了简便,N的自然对数 简记作lnN。 简记作ln3 ; 简记作ln10基本概念为了简便,N的常用对数 简记作lgN。 简记作lg3.5. 课堂练习:阅读教材P75----P76
然后完成书P76 练习 :1, 2 例题2,计算下列各式。 则 解:设 解:设 则 思考3:loga1=? logaa=? 01练习,计算下列各式。=1=01.知识点小结:
本节课学习了对数的概念以
及指数式与对数式互相转化课堂小结:2.思想方法小结:
逆向思维
用联系的观点看问题
布置作业1)阅读教材P80的阅读材料,进一步了解对数
的发明过程。2)书P79 习题2.7 1 2
课外思考题再见谢谢各位专家指导 对数的创始人是苏格兰数学家纳皮尔(Napier,1550年~1617年)。在纳皮尔所处的年代,哥白尼的“太阳中心说”刚刚开始流行,这导致天文学成为当时的热门学科。可是由于当时常量数学的局限性,天文学家们不得不花费很大的精力去计算那些繁杂的“天文数字”,因此浪费了若干年甚至毕生的宝贵时间。纳皮尔也是当时的一位天文爱好者,为了简化计算,他多年潜心研究大数字的计算技术,终于独立发明了对数。
