二北师版数学必修1次函数的图象

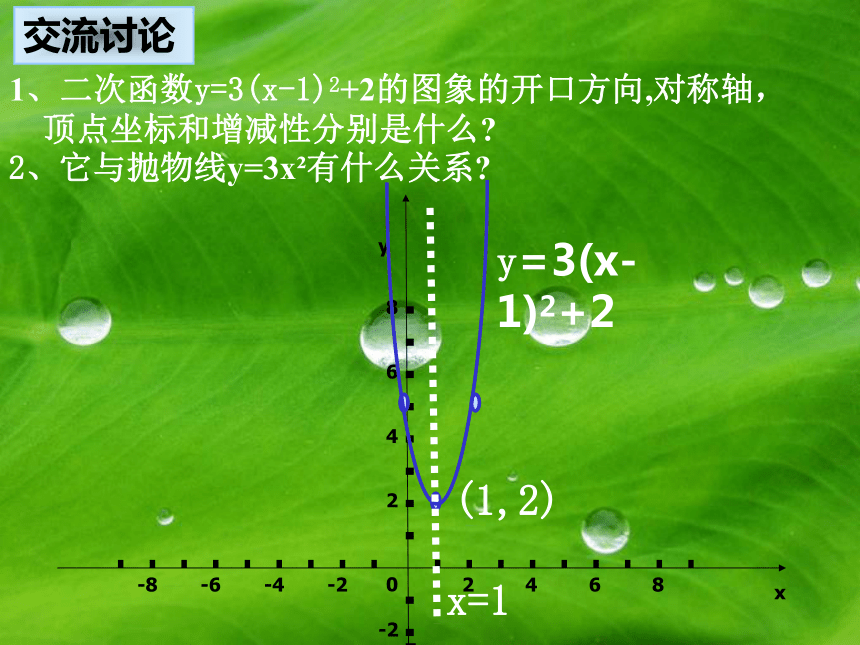
课件18张PPT。荀青松灵宝市第一初级中学二次函数y=ax2+bx+c的图象和性质xy 二次函数y= ３x2-６x+５的图象是什么形状，它与我们已经作过的二次函数的图象有什么关系？解：y=3x2-6x+5=3(x-1)2+2列表：描点、连线： 探索新知y=3(x-1)2+22、它与抛物线y=3x2有什么关系?x=1(1,2)二次函数y=a(x-h)2+k与y=ax2的关系y=ax2
(a≠0)
y=ax2+k
(a≠0)y=a(x-h)2
(a≠0)y=a(x-h)2+k
(a≠0)沿对称轴上(下)
平移|k|个单位沿x轴左(右)
平移|h|个单位再向左(右)平移|h|个单位沿对称轴上(下)
平移|k|个单位注：上正下负，左负右正。1、抛物线y=-2(x+3)2-1的开口向（ ），对称轴为（ ），顶点坐标为（ ），x（ ）时，y随x的增大而增大。
2、二次函数 化为y=a(x-h)2+k的形式是（ ）
3、抛物线y=3x2先向上平移2个单位，后向右平移3个单位，所得到的抛物线是（ ） 　A、y=3(x+3)2-2 B、 y=3(x+3)2+2 　C、y=3(x-3)2-2 D、 y=3(x-3)2+2
4、某二次函数的图象向左平移2个单位，然后向上平移3个单位后，得到的函数表达式是y=2x2， 则原函数表达式是( )。
下x= -3(-3,-1)<-3ADy=2(x-2)2-3BC二次函数y=a(x-h)2+k与y=ax2的关系y=ax2
(a≠0)
y=ax2+k
(a≠0)y=a(x-h)2
(a≠0)y=a(x-h)2+k
(a≠0)沿对称轴上(下)
平移|k|个单位沿x轴左(右)
平移|h|个单位再向左(右)平移|h|个单位沿对称轴上(下)
平移|k|个单位注：上正下负，左正右负。 互动探究，拓展延伸 心理学家发现，学生对概念的接受能力y与提出概念所用的时间（单位：min)之间满足函数关系y= - 0.1x2+2.6x+43(0≤x ≤30),y值越大，表示接受能力越强。
（1）x在什么范围内，学生的接受能力逐步增强？x在什么范围内，学生的接受能力逐步降低？ （2）第10min时，学生的接受能力是多少？ （ 3）多长时间时，学生的接受能力最强？(1)当0≤x ≤13时, 学生的接受能力逐步增强;当13≤x ≤30时, 学生的接受能力逐步降低。(2)当x=10时，y=59。(3)当x=13时，学生的接受能力最强为59.9。解: y= - 0.1(x-13)2+59.9回味无穷：
1、抛物线y=-x2-1的开口向（　　），对称轴是（ ），顶点坐标是（ ），在对称轴的左侧，y随x的增大而（ ），在右侧，y随x的增大而（ ），可由y=-x2沿（　　）轴向（ ）平移（ ）个单位而得到。
2、抛物线y=２（x-３）2的开口向（　　），对称轴是（ ），顶点坐标是（ ），在对称轴的左侧，y随x的增大而（ ），在右侧，y随x的增大而（ ），可由y= ２x2沿（　　）轴向（ ）平移（ ）个单位而得到。