1.1分类加法计数原理与分步乘法计数原理2
文档属性
| 名称 | 1.1分类加法计数原理与分步乘法计数原理2 |

|
|
| 格式 | rar | ||
| 文件大小 | 222.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-27 00:00:00 | ||
图片预览





文档简介
课件15张PPT。1.1 分类加法计数原理
与分步乘法计数原理
(第二课时)1. 分类加法计数原理:完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法, ……,在第n类方案中有mn种不同的方法.那么完成这件事共有N=m1+m2+…+mn种不同的方法.2.分步乘法计数原理:完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步有mn种不同的方法.那么完成这件事共有N=m1+m2+…+mn种不同的方法.两个原理 应用分类计数有条理和分步计数原理解题策略:
1.搞清要完成的“一件事”是什么;
2.是分类完成还是分步完成,
“类”间互相独立,“步”间互相关联;
3.有无特殊条件的限制.1. 有一个袋子里装有不同编号的红色小球6个,白色小球5个和黄色小球4个,
(1) 从袋子里任取一个小球,不同的取法有 种;
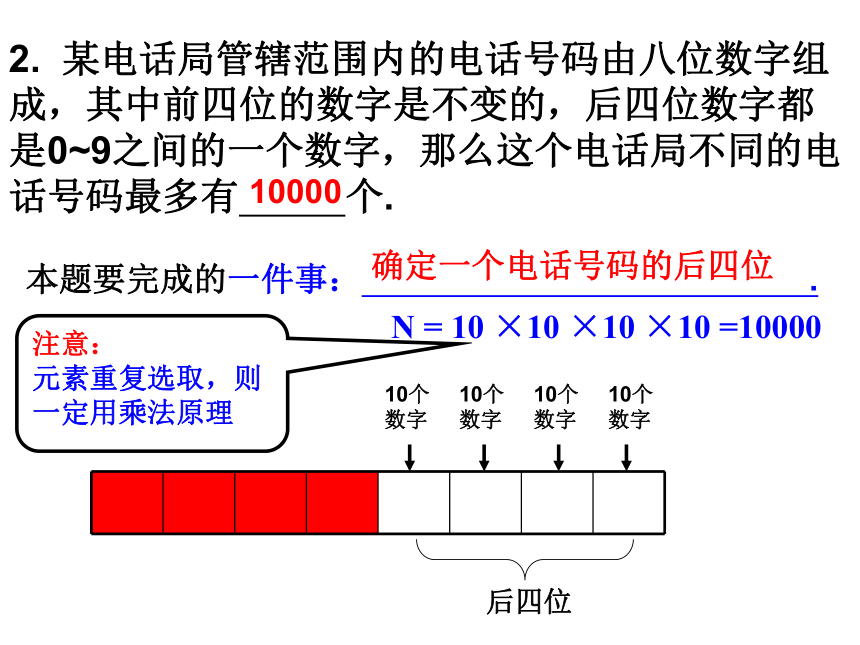
(2) 从袋子里任取红、白、黄小球各1个,不同的取法有 种.课前练习15120 本题要完成的一件事: . 本题要完成的一件事: . 取一个小球取一个红球、一个白球和一个黄球N = 6 ×5 ×4 =120N = 6 + 5 + 4 =152. 某电话局管辖范围内的电话号码由八位数字组成,其中前四位的数字是不变的,后四位数字都是0~9之间的一个数字,那么这个电话局不同的电话号码最多有 个.后四位10个数字10个数字10个数字10个数字本题要完成的一件事: . 确定一个电话号码的后四位注意:
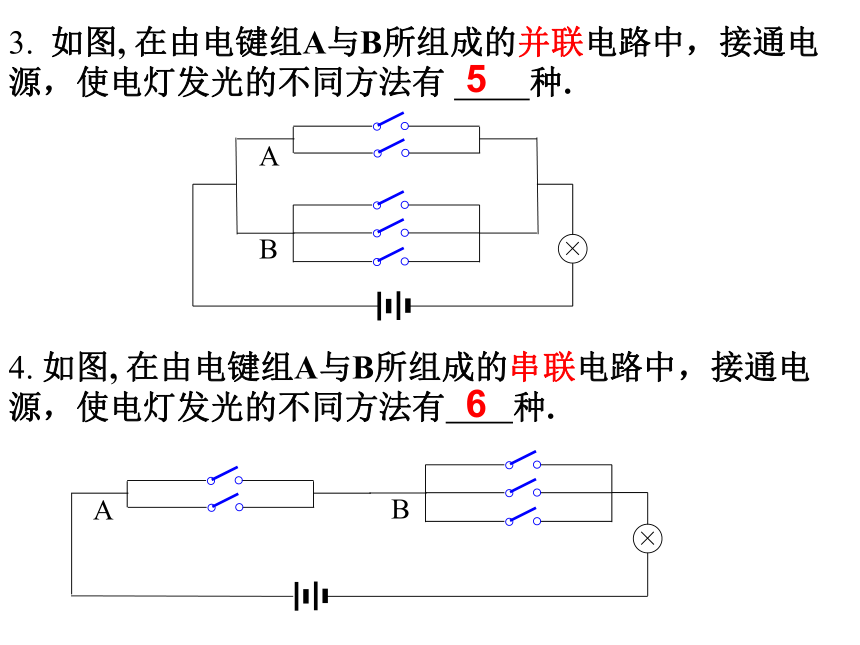
元素重复选取,则一定用乘法原理10000N = 10 ×10 ×10 ×10 =100003. 如图, 在由电键组A与B所组成的并联电路中,接通电源,使电灯发光的不同方法有 种.4. 如图, 在由电键组A与B所组成的串联电路中,接通电源,使电灯发光的不同方法有 种.56例5. 给程序模块命名,需要用3个字符,其中首个字符要求用字母A~G或U~Z,后两个要求用数字1~9,问最多可以给多少个程序命名?分析:要给一个程序模块命名,可以分3个步骤:第1步,选首字符;第2步,先中间字符;第3步,选末位字符。解:首字符共有7+6=13种不同的选法,答:最多可以给1053个程序命名。 中间字符和末位字符各有9种不同的选法 根据分步乘法计数原理,最多可以有13×9×9=1053种不同的选法.例题解析本题要完成的一件事: . 选3个字符给一个程序模块命名你还有其他的解法吗?例6. 核糖核酸(RNA)分子是在生物细胞中发现的化学成分,一个RNA分子是一个有着数百个甚至数千个位置的长链,长链中每一个位置上都由一种称为碱基的化学成分所占据,总共有4个不同的碱基,分别用A,C,G,U表示,在一个RNA分子中,各种碱基能够以任意次序出现,所以在任意一个位置上的碱基与其他位置上的碱基无关。假设有一类RNA分子由100个碱基组成,那么能有多少种不同的RNA分子?例6. 核糖核酸(RNA)分子是在生物细胞中发现的化学成分,一个RNA分子是一个有着数百个甚至数千个位置的长链,长链中每一个位置上都由一种称为碱基的化学成分所占据,总共有4个不同的碱基,分别用A,C,G,U表示,在一个RNA分子中,各种碱基能够以任意次序出现,所以在任意一个位置上的碱基与其他位置上的碱基无关。假设有一类RNA分子由100个碱基组成,那么能有多少种不同的RNA分子?分析:用100个位置表示由100个碱基组成的长链,每个位置都可以从A、C、G、U中任选一个来占据。……解:100个碱基组成的长链共有100个位置,在每个位置中,从A、C、G、U中任选一个来填入,每个位置有4种填充方法。根据分步计数原理,共有种不同的RNA分子.100个位置中每个位置要得到一个RNA分子本题要完成的一件事: . 随堂练习2. 从5名同学中选出正、副组长各1名,有 种不同的选法。3. 某商场有6个门,如果某人从其中的任意一个门进入商场,并且要求从其他的门出去,共有 种不同的进出商场的方式。N = 3×4×5 = 60N = 5×4 = 20N = 6×5 = 304. 如图,从甲地到乙地有2条路可通,从乙地到丙地有3条路可通;从甲地到丁地有4条路可通, 从丁地到丙地有2条路可通。从甲地到丙地共有多少种不同的走法? 解:从总体上看,由甲到丙有两类不同的走法,
第一类, 由甲经乙去丙,又需分两步, 所以 m1 = 2×3 = 6 种不同的走法;
第二类, 由甲经丁去丙,也需分两步, 所以 m2 = 4×2 = 8 种不同的走法;
所以从甲地到丙地共有
N = 6 + 8 = 14 种不同的走法。思考:如图, 要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?解: 按地图A、B、C、D四个区域依次分四步完成,
第一步, m1 = 3 种,
第二步, m2 = 2 种,
第三步, m3 = 1 种,
第四步, m4 = 1 种,
所以根据乘法原理, 得到不同的涂色方案种数共有 N = 3 × 2 ×1×1 = 6 种。
变式:如图,要给地图A、B、C、D四个区域分别涂上4 种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种? 答:不同的涂色方案种数有 4×3×2×2 = 48种 用两个计数原理解决计数问题时,最重要的是在开始计算之前要进行仔细分析——
需要分类还是需要分步. 分类要做到“不重不漏”. 分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数. 分步要做到“步骤完整”.完成所有步骤,恰好完成任务,当然步与步之间要相互独立. 分步后再计算每一步的方法数,最后用分步乘法计数原理相乘,得到总数.思考? 你能归纳一下用分类加法计数原理、分步乘法计数原理解决计数问题的方法吗?
(第二课时)1. 分类加法计数原理:完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法, ……,在第n类方案中有mn种不同的方法.那么完成这件事共有N=m1+m2+…+mn种不同的方法.2.分步乘法计数原理:完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步有mn种不同的方法.那么完成这件事共有N=m1+m2+…+mn种不同的方法.两个原理 应用分类计数有条理和分步计数原理解题策略:
1.搞清要完成的“一件事”是什么;
2.是分类完成还是分步完成,
“类”间互相独立,“步”间互相关联;
3.有无特殊条件的限制.1. 有一个袋子里装有不同编号的红色小球6个,白色小球5个和黄色小球4个,
(1) 从袋子里任取一个小球,不同的取法有 种;
(2) 从袋子里任取红、白、黄小球各1个,不同的取法有 种.课前练习15120 本题要完成的一件事: . 本题要完成的一件事: . 取一个小球取一个红球、一个白球和一个黄球N = 6 ×5 ×4 =120N = 6 + 5 + 4 =152. 某电话局管辖范围内的电话号码由八位数字组成,其中前四位的数字是不变的,后四位数字都是0~9之间的一个数字,那么这个电话局不同的电话号码最多有 个.后四位10个数字10个数字10个数字10个数字本题要完成的一件事: . 确定一个电话号码的后四位注意:
元素重复选取,则一定用乘法原理10000N = 10 ×10 ×10 ×10 =100003. 如图, 在由电键组A与B所组成的并联电路中,接通电源,使电灯发光的不同方法有 种.4. 如图, 在由电键组A与B所组成的串联电路中,接通电源,使电灯发光的不同方法有 种.56例5. 给程序模块命名,需要用3个字符,其中首个字符要求用字母A~G或U~Z,后两个要求用数字1~9,问最多可以给多少个程序命名?分析:要给一个程序模块命名,可以分3个步骤:第1步,选首字符;第2步,先中间字符;第3步,选末位字符。解:首字符共有7+6=13种不同的选法,答:最多可以给1053个程序命名。 中间字符和末位字符各有9种不同的选法 根据分步乘法计数原理,最多可以有13×9×9=1053种不同的选法.例题解析本题要完成的一件事: . 选3个字符给一个程序模块命名你还有其他的解法吗?例6. 核糖核酸(RNA)分子是在生物细胞中发现的化学成分,一个RNA分子是一个有着数百个甚至数千个位置的长链,长链中每一个位置上都由一种称为碱基的化学成分所占据,总共有4个不同的碱基,分别用A,C,G,U表示,在一个RNA分子中,各种碱基能够以任意次序出现,所以在任意一个位置上的碱基与其他位置上的碱基无关。假设有一类RNA分子由100个碱基组成,那么能有多少种不同的RNA分子?例6. 核糖核酸(RNA)分子是在生物细胞中发现的化学成分,一个RNA分子是一个有着数百个甚至数千个位置的长链,长链中每一个位置上都由一种称为碱基的化学成分所占据,总共有4个不同的碱基,分别用A,C,G,U表示,在一个RNA分子中,各种碱基能够以任意次序出现,所以在任意一个位置上的碱基与其他位置上的碱基无关。假设有一类RNA分子由100个碱基组成,那么能有多少种不同的RNA分子?分析:用100个位置表示由100个碱基组成的长链,每个位置都可以从A、C、G、U中任选一个来占据。……解:100个碱基组成的长链共有100个位置,在每个位置中,从A、C、G、U中任选一个来填入,每个位置有4种填充方法。根据分步计数原理,共有种不同的RNA分子.100个位置中每个位置要得到一个RNA分子本题要完成的一件事: . 随堂练习2. 从5名同学中选出正、副组长各1名,有 种不同的选法。3. 某商场有6个门,如果某人从其中的任意一个门进入商场,并且要求从其他的门出去,共有 种不同的进出商场的方式。N = 3×4×5 = 60N = 5×4 = 20N = 6×5 = 304. 如图,从甲地到乙地有2条路可通,从乙地到丙地有3条路可通;从甲地到丁地有4条路可通, 从丁地到丙地有2条路可通。从甲地到丙地共有多少种不同的走法? 解:从总体上看,由甲到丙有两类不同的走法,
第一类, 由甲经乙去丙,又需分两步, 所以 m1 = 2×3 = 6 种不同的走法;
第二类, 由甲经丁去丙,也需分两步, 所以 m2 = 4×2 = 8 种不同的走法;
所以从甲地到丙地共有
N = 6 + 8 = 14 种不同的走法。思考:如图, 要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?解: 按地图A、B、C、D四个区域依次分四步完成,
第一步, m1 = 3 种,
第二步, m2 = 2 种,
第三步, m3 = 1 种,
第四步, m4 = 1 种,
所以根据乘法原理, 得到不同的涂色方案种数共有 N = 3 × 2 ×1×1 = 6 种。
变式:如图,要给地图A、B、C、D四个区域分别涂上4 种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种? 答:不同的涂色方案种数有 4×3×2×2 = 48种 用两个计数原理解决计数问题时,最重要的是在开始计算之前要进行仔细分析——
需要分类还是需要分步. 分类要做到“不重不漏”. 分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数. 分步要做到“步骤完整”.完成所有步骤,恰好完成任务,当然步与步之间要相互独立. 分步后再计算每一步的方法数,最后用分步乘法计数原理相乘,得到总数.思考? 你能归纳一下用分类加法计数原理、分步乘法计数原理解决计数问题的方法吗?
