人教b版必修1数学:第1章集合 111集合的概念
文档属性
| 名称 | 人教b版必修1数学:第1章集合 111集合的概念 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-25 00:00:00 | ||
图片预览








文档简介
课件20张PPT。1.1 集合与集合的表示方法
1.1.1 集合的概念 1.列出满足“大于5而小于10”的所有整数 .
2.初中时接触过一些集合,你还记得“自然数的集合”、“有理数的集合”的含义吗?自然数的集合包含: ,有理数的集合包含: .
3.你还会求不等式x+2>3的解集吗?
解集为: .
4.到一个定点的距离等于定长的点的集合是 .6、7、8、90和正整数整数和分数x>1圆 1.集合
(1)集合:把一些能够 对象看成一个整体,这个整体是由这些对象的 构成的集合(或集).通常用
表示.
(2)元素:构成集合的每个对象叫做这个集合的元素(或成员),通常用 表示.
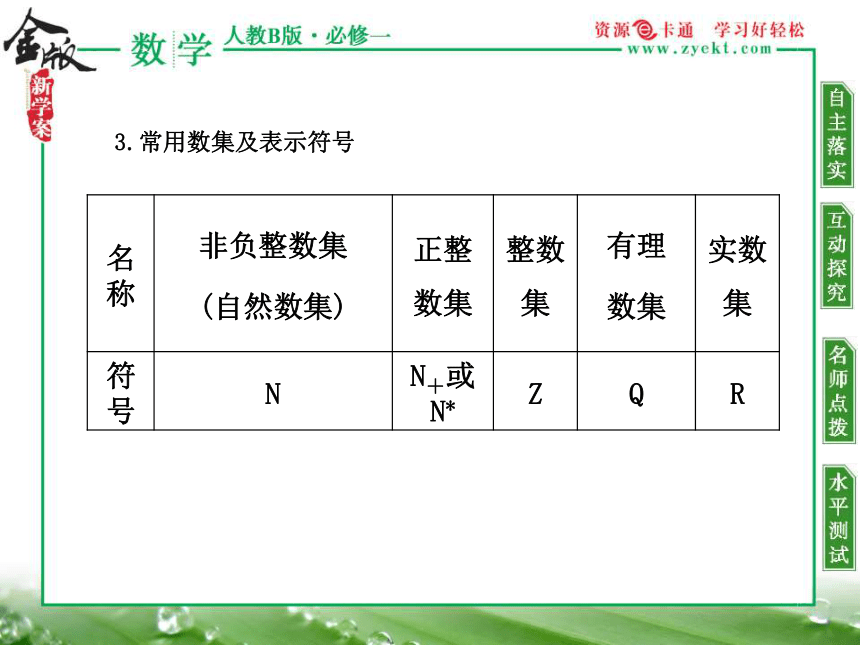
(3)集合元素的特性: 、 、无序性.确定的不同全体英语大写字母英语小写字母确定性互异性2.元素与集合的关系3.常用数集及表示符号
如何判断一组对象是否构成集合?
【提示】 关键是看判断对象的标准是否确定.考察下列每组对象能否组成一个集合.
(1)美丽的小鸟;
(2)不超过20的非负整数;
(3)立方接近零的正数;
(4)直角坐标系中,第一象限内的点. 【思路点拨】 解答本题可先分析各组的对象是否具有确定性和互异性,再作出判断.
【解析】 (1)中“美丽”的范畴太广,不具有集合元素的确定性,因此不能组成集合;
(2)中的元素可以列举出来:0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,共21个数;
(3)中接近0的界限不明确;
(4)中元素具有无限个,但条件明确,即所有横、纵坐标均大于0的点均在该集合中.
综上可知(2)(4)能组成集合;(1)(3)不能组成集合. 判定元素能否组成集合,关键看这些元素是否具有确定性和互异性.如果条件满足就可以断定这些元素可以组成集合,否则不能组成集合. 1.下列说法正确的是( )
A.某班中年龄较小的同学组成一个集合
B.分别由1,2,3和3,1,2组成的集合表示不同集合
C.参加2008年北京奥运会的所有中国运动员组成一个集合 【解析】 A中元素不确定;B中两个集合元素相同,因集合元素具有无序性,所以两个集合相等;C中元素明确、具体,可以组成集合;D中元素0.5和 是一个元素,由元素互异性知,元素个数应为三.
【答案】 C 已知集合A={a-3,2a-1,a2-4},且-3∈A,求实数a的值.
【思路点拨】 因为-3∈A,所以集合A中必有一元素为-3. 【解析】 ∵-3∈A,A={a-3,2a-1,a2-4},
∴a-3=-3,或2a-1=-3,或a2-4=-3.
若a-3=-3,则a=0,此时集合A={-3,-1,-4},符合题意.
若2a-1=-3,则a=-1,此时集合A={-4,-3,-3},
不满足集合中元素的互异性.
若a2-4=-3,则a=1,或a=-1(舍去),
当a=1时,集合A={-2,1.-3},符合题意.
综上可知,a=0,或a=1. 集合中元素的三个特性,尤其是互异性,在解题中应用较多.一般在解出结果后都需要进行互异性检验.若集合中出现重复元素便只留其一,舍弃多余的. 2.已知集合A由1,x,x2三个元素构成,集合B由1,2,x三个元素构成,若集合A与集合B相等,求x的值 【解析】 因为集合A与集合B相等, 设集合A={x|x=2k,k∈Z},B={x|x=2k+1,k∈Z}.若a∈A,b∈B,试判断a+b与A,B的关系.
【思路点拨】 因为A是偶数集,B是奇数集,所以a是偶数,b是奇数,从而a+b是奇数.【解析】 ∵a∈A,∴a=2k1(k1∈Z).
∵b∈B,∴b=2k2+1(k2∈Z).
∴a+b=2(k1+k2)+1.
又∵k1+k2∈Z,
∴a+b∈B,从而a+b?A. 判断一个元素是不是某个集合的元素,就是判断这个对象是不是具有这个集合的元素所具有的特征性质,反之,如果一个元素是某个集合的元素,这个元素也一定具有这个集合中元素共有的特征性质.【解析】 1.集合的概念可以从以下几个方面来理解
(1)集合是一个“整体”;
(2)构成集合的对象必须具有“确定”且“不同”这两个特征.这两个特征不是模棱两可的.
判定一组对象能否构成一个集合,关键要看是否有一个明确的客观标准来鉴定这些对象,若鉴定对象确定的客观标准存在,则这些对象就能构成集合,否则不能构成集合. 2.对集合中元素三个特性的认识
(1)确定性:指的是作为一个集合中元素,必须是确定的.即一个集合一旦确定,某一个元素属于或不属于这个集合是确定的.要么是该集合中的元素要么不是,二者必居其一,这个特性通常被用来判断涉及的总体是否构成集合.
(2)互异性:集合中的元素必须是互异的,就是说,对于一个给定的集合,它的任何两个元素都是不同的.如方程(x-1)2=0的解构成的集合为{1},而不能记为{1,1}.这个特性通常被用来判断集合的表示是否正确,或用来求集合中的未知元素.
(3)无序性:集合与其中元素的排列顺序无关,如集合{a,b,c}与{b,a,c}是相等的集合.这个特性通常用来判断两个集合的关系. 写出方程x2-(a+1)x+a=0的解的集合.
【错解】 x2-(a+1)x+a=(x-a)(x-1)=0,所以解为x=1或x=a,解集为{1,a}.
【错因】 方程的解集不能简单的直接写为{1,a},由于a是不确定的参数,当a的取值不同时,解集有可能不相同,因此,要对a进行讨论.
【正解】 x2-(a+1)x+a=(x-a)(x-1)=0,所以解为x=1或x=a.若a=1,则解集为{1};若a≠1,则解集为{1,a}.进入备考水平测试
1.1.1 集合的概念 1.列出满足“大于5而小于10”的所有整数 .
2.初中时接触过一些集合,你还记得“自然数的集合”、“有理数的集合”的含义吗?自然数的集合包含: ,有理数的集合包含: .
3.你还会求不等式x+2>3的解集吗?
解集为: .
4.到一个定点的距离等于定长的点的集合是 .6、7、8、90和正整数整数和分数x>1圆 1.集合
(1)集合:把一些能够 对象看成一个整体,这个整体是由这些对象的 构成的集合(或集).通常用
表示.
(2)元素:构成集合的每个对象叫做这个集合的元素(或成员),通常用 表示.
(3)集合元素的特性: 、 、无序性.确定的不同全体英语大写字母英语小写字母确定性互异性2.元素与集合的关系3.常用数集及表示符号
如何判断一组对象是否构成集合?
【提示】 关键是看判断对象的标准是否确定.考察下列每组对象能否组成一个集合.
(1)美丽的小鸟;
(2)不超过20的非负整数;
(3)立方接近零的正数;
(4)直角坐标系中,第一象限内的点. 【思路点拨】 解答本题可先分析各组的对象是否具有确定性和互异性,再作出判断.
【解析】 (1)中“美丽”的范畴太广,不具有集合元素的确定性,因此不能组成集合;
(2)中的元素可以列举出来:0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,共21个数;
(3)中接近0的界限不明确;
(4)中元素具有无限个,但条件明确,即所有横、纵坐标均大于0的点均在该集合中.
综上可知(2)(4)能组成集合;(1)(3)不能组成集合. 判定元素能否组成集合,关键看这些元素是否具有确定性和互异性.如果条件满足就可以断定这些元素可以组成集合,否则不能组成集合. 1.下列说法正确的是( )
A.某班中年龄较小的同学组成一个集合
B.分别由1,2,3和3,1,2组成的集合表示不同集合
C.参加2008年北京奥运会的所有中国运动员组成一个集合 【解析】 A中元素不确定;B中两个集合元素相同,因集合元素具有无序性,所以两个集合相等;C中元素明确、具体,可以组成集合;D中元素0.5和 是一个元素,由元素互异性知,元素个数应为三.
【答案】 C 已知集合A={a-3,2a-1,a2-4},且-3∈A,求实数a的值.
【思路点拨】 因为-3∈A,所以集合A中必有一元素为-3. 【解析】 ∵-3∈A,A={a-3,2a-1,a2-4},
∴a-3=-3,或2a-1=-3,或a2-4=-3.
若a-3=-3,则a=0,此时集合A={-3,-1,-4},符合题意.
若2a-1=-3,则a=-1,此时集合A={-4,-3,-3},
不满足集合中元素的互异性.
若a2-4=-3,则a=1,或a=-1(舍去),
当a=1时,集合A={-2,1.-3},符合题意.
综上可知,a=0,或a=1. 集合中元素的三个特性,尤其是互异性,在解题中应用较多.一般在解出结果后都需要进行互异性检验.若集合中出现重复元素便只留其一,舍弃多余的. 2.已知集合A由1,x,x2三个元素构成,集合B由1,2,x三个元素构成,若集合A与集合B相等,求x的值 【解析】 因为集合A与集合B相等, 设集合A={x|x=2k,k∈Z},B={x|x=2k+1,k∈Z}.若a∈A,b∈B,试判断a+b与A,B的关系.
【思路点拨】 因为A是偶数集,B是奇数集,所以a是偶数,b是奇数,从而a+b是奇数.【解析】 ∵a∈A,∴a=2k1(k1∈Z).
∵b∈B,∴b=2k2+1(k2∈Z).
∴a+b=2(k1+k2)+1.
又∵k1+k2∈Z,
∴a+b∈B,从而a+b?A. 判断一个元素是不是某个集合的元素,就是判断这个对象是不是具有这个集合的元素所具有的特征性质,反之,如果一个元素是某个集合的元素,这个元素也一定具有这个集合中元素共有的特征性质.【解析】 1.集合的概念可以从以下几个方面来理解
(1)集合是一个“整体”;
(2)构成集合的对象必须具有“确定”且“不同”这两个特征.这两个特征不是模棱两可的.
判定一组对象能否构成一个集合,关键要看是否有一个明确的客观标准来鉴定这些对象,若鉴定对象确定的客观标准存在,则这些对象就能构成集合,否则不能构成集合. 2.对集合中元素三个特性的认识
(1)确定性:指的是作为一个集合中元素,必须是确定的.即一个集合一旦确定,某一个元素属于或不属于这个集合是确定的.要么是该集合中的元素要么不是,二者必居其一,这个特性通常被用来判断涉及的总体是否构成集合.
(2)互异性:集合中的元素必须是互异的,就是说,对于一个给定的集合,它的任何两个元素都是不同的.如方程(x-1)2=0的解构成的集合为{1},而不能记为{1,1}.这个特性通常被用来判断集合的表示是否正确,或用来求集合中的未知元素.
(3)无序性:集合与其中元素的排列顺序无关,如集合{a,b,c}与{b,a,c}是相等的集合.这个特性通常用来判断两个集合的关系. 写出方程x2-(a+1)x+a=0的解的集合.
【错解】 x2-(a+1)x+a=(x-a)(x-1)=0,所以解为x=1或x=a,解集为{1,a}.
【错因】 方程的解集不能简单的直接写为{1,a},由于a是不确定的参数,当a的取值不同时,解集有可能不相同,因此,要对a进行讨论.
【正解】 x2-(a+1)x+a=(x-a)(x-1)=0,所以解为x=1或x=a.若a=1,则解集为{1};若a≠1,则解集为{1,a}.进入备考水平测试
