人教b版必修1数学:第1章集合 122集合的运算
文档属性
| 名称 | 人教b版必修1数学:第1章集合 122集合的运算 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-25 19:30:00 | ||
图片预览







文档简介
课件22张PPT。1.2.2 集合的运算 1.“集合A是集合B的子集”的含义是 .
2.若A?B,且B?A,则 ,反过来,要证A=B,只要证 且 即可.
3.空集是任何集合的 ,是任何非空集合
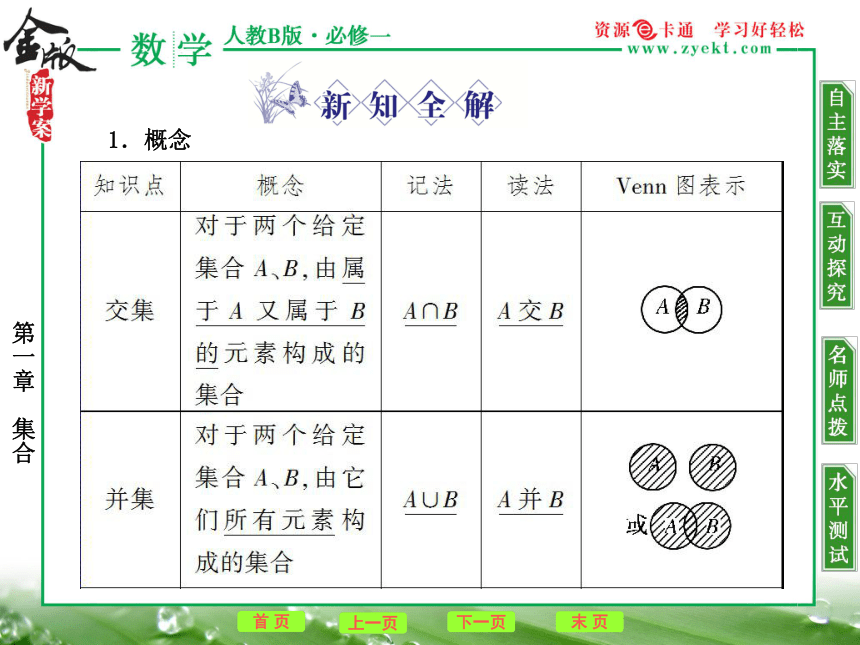
的 .A中的元素全在B中A=BA?BB?A子集真子集1.概念2.运算性质
(1)交集的运算性质
① ,② ,
③ ,④如果A?B,则 .
(2)并集的运算性质
①A∪B=B∪A,②A∪A=A
③A∪?=?∪A=A,④如果A?B,则 .
(3)补集的运算性质
① ,② ,③ .A∩B=B∩AA∩A=AA∩?=?∩A=?A∩B=AA∪B=BA∪?UA=UA∩?UA=??U(?UA)=A 1.能否认为A与B没有公共元素时,A与B就没有交集?
【提示】 不能.当A与B无公共元素时,A与B的交集仍存在,此时A∩B=?.
2.如何确定一个集合的补集?
【提示】 确定一个集合的补集时,首先要确定全集U是什么,?UA是“A在U中的补集”,这里包含着两重含义:一是A必须是U的子集;二是?UA是由U中不属于A的所有元素组成的集合,即?UA={x|x∈U,且x?A}.已知S={x|2x2-px+q=0},T={x|6x2+(p+2)x+q+5=0},【思路点拨】【解析】 正确理解并集、交集的概念是进行集合运算的基础,两个集合的交集,就是由两个集合的公共元素组成的集合;并集就是将两集合的元素放在一起组成的集合. 1.已知集合A={2,m},B={3,m2},若A∪B={1,2,3,m},求m的值.
【解析】 由A∪B中含有4个元素可知,m2≠m,
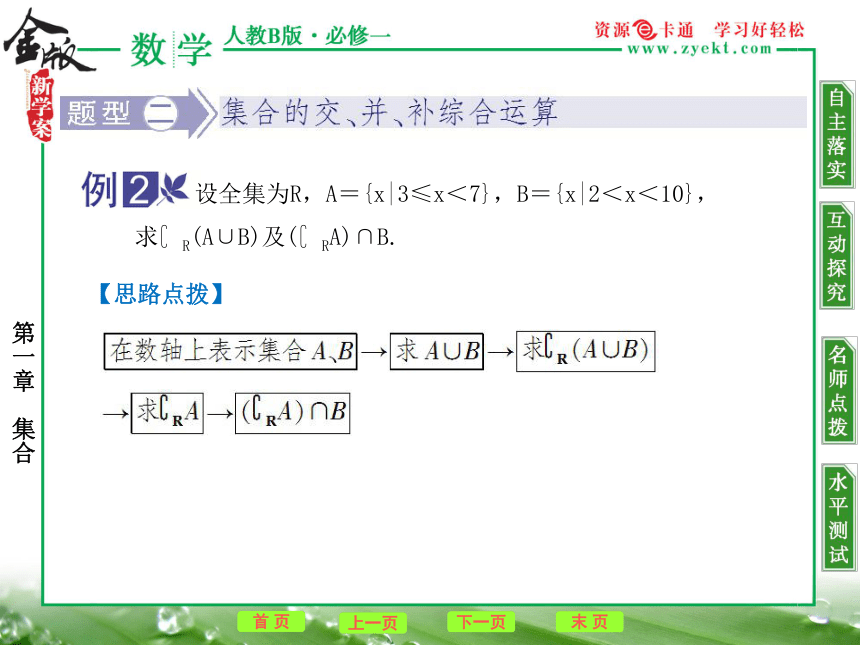
∴m≠0且m≠1,∴m2=1,∴m=-1. 设全集为R,A={x|3≤x<7},B={x|2<x<10},
求?R(A∪B)及(?RA)∩B.【思路点拨】【解析】 把全集R和集合A、B在数轴上表示如下:由图知,A∪B={x|2<x<10},
∴?R(A∪B)={x|x≤2或x≥10}.
∵?RA={x|x<3或x≥7},
∴(?RA)∩B={x|2<x<3或7≤x<10}. (1)数轴与Venn图有同样的直观功效,在数轴上可以直观表示数集,所以进行集合的交、并、补运算时,经常在数轴上进行表示.
(2)交集、并集、补集还有如下关系:
?U(A∩B)=(?UA)∪(?UB),?U(A∪B)=(?UA)∩(?UB).
2.已知全集U={x|x≤5},集合A={x|-2<x<2},B={x|-3<x≤3}.求?UA,A∩B,?U(A∩B),(?UA)∩B. 【思路点拨】 由题目可获取以下主要信息:①全集U,集合A、B均为无限集;②所求问题为集合间交、并、补运算.解答此题可借助数轴求解.
由图可知,
?UA={x|x≤-2或2≤x≤5},
A∩B={x|-2<x<2},
?U(A∩B)={x|x≤-2或2≤x≤4},
(?UA)∩B={x|-3<x≤-2或2≤x≤3}.【解析】 把全集U和集合A,B在数轴上表示如下: 已知全集U={1,2,3,4,5}.A={x|x2-5x+m=0},B={x|x2+nx+12=0},且?UA∪B={1,3,4,5},求m+n的值.
【思路点拨】 A、B是由一元二次方程的根为元素组成的集合,又?UA∪B={1,3,4,5},故2∈A.【解析】 ∵U={1,2,3,4,5},?UA∪B={1,3,4,5},
∴2∈A,又A={x|x2-5x+m=0},
∴2是关于x的方程x2-5x+m=0的一个根,
得m=6且A={2,3},
∴?UA={1,4,5}.而?UA∪B={1,3,4,5},
∴3∈B,又B={x|x2+nx+12=0},
∴3一定是关于x的方程x2+nx+12=0的一个根.
∴n=-7且B={3,4},∴m+n=-1. 正确理解条件?UA∪B={1,3,4,5}是解题的关键,解决此类问题时,可以借助Venn图辅助求解,结合已知条件明确一些元素的具体分布区域.
3.已知集合A={x|x2+ax+12b=0}和B={x|x2-ax+b=0},满足(?UA)∩B={2},A∩(?UB)={4},U=R,求实数a,b的值.
【解析】 ∵(?UA)∩B={2},
∴2∈B,但2?A.
∵A∩(?UB)={4},∴4∈A,但4?B.
∴ ∴a= ,b= . 1.对并集概念的理解
(1)定义中的“x∈A,或x∈B”包含三种情况:“x∈A,但x?B”;“x∈B,但x?A”;“x∈A,且x∈B”.Venn图如图所示.另外,在求两个集合的并集时,它们的公共元素只出现一次.
(2)并集在定义中是由集合A与B的所有元素组成的集合,从这个意义上讲,A∪B可以类比实数的加法运算.2.对交集概念的理解 (1)并不是任何两个集合都有公共元素,当集合A与B没有公共元素时,不能说A与B没有交集,而是A∩B=?.如图所示.
(2)定义中的“所有”两字的含义是,不仅“A∩B中的任意元素都是A与B的公共元素”,同时还有“A与B的公共元素都属于A∩B”. (3)全集含有所要研究的集合的所有元素,因此,全集是对所研究问题而言的相对概念.全集既可以是无限集,也可以是有限集. 3.关于全集与补集
(1)补集与全集是两个密不可分的概念,同一个集合在不同的全集中补集是不同的,不同的集合在同一个全集中的补集也不同.另外全集是一个相对概念.
(2)?UA的数学意义包括两个方面:首先必须具备A?U,其次是运用“元素分析法”定义?UA={x|x∈U,且x?A},补集是集合间的运算关系,这可以和实数的减法相类比.4.补集的性质
根据补集的定义,补集仍是一个集合,显然有以下性质:
(1)?AA=?,?A?=A.
(2)?U(?UA)=A.
(3)A∪?UA=U,A∩?UA=?. 设集合A={x∈R|x2+2x+2-p=0},且A∩{x|x>0}=?,求实数p的取值范围. 【错解】 依题意,方程x2+2x+2-p=0没有实数解,因此Δ=22-4(2-p)<0,解得p<1.所以实数p的取值范围为{p|p<1}.
【错因】 A∩{x|x>0}=?,表示方程x2+2x+2-p=0没有正实数解,此时等价于方程没有实数解或有非正实数解,本题错解中由于没有正确理解这一集合语言,而造成错误.我们在解题时应避免出现这种由于对题意把握不准而造成的错误.【正解】 由题意,若A=?,即Δ=22-4(2-p)<0,所以p<1.进入备考水平测试
2.若A?B,且B?A,则 ,反过来,要证A=B,只要证 且 即可.
3.空集是任何集合的 ,是任何非空集合
的 .A中的元素全在B中A=BA?BB?A子集真子集1.概念2.运算性质
(1)交集的运算性质
① ,② ,
③ ,④如果A?B,则 .
(2)并集的运算性质
①A∪B=B∪A,②A∪A=A
③A∪?=?∪A=A,④如果A?B,则 .
(3)补集的运算性质
① ,② ,③ .A∩B=B∩AA∩A=AA∩?=?∩A=?A∩B=AA∪B=BA∪?UA=UA∩?UA=??U(?UA)=A 1.能否认为A与B没有公共元素时,A与B就没有交集?
【提示】 不能.当A与B无公共元素时,A与B的交集仍存在,此时A∩B=?.
2.如何确定一个集合的补集?
【提示】 确定一个集合的补集时,首先要确定全集U是什么,?UA是“A在U中的补集”,这里包含着两重含义:一是A必须是U的子集;二是?UA是由U中不属于A的所有元素组成的集合,即?UA={x|x∈U,且x?A}.已知S={x|2x2-px+q=0},T={x|6x2+(p+2)x+q+5=0},【思路点拨】【解析】 正确理解并集、交集的概念是进行集合运算的基础,两个集合的交集,就是由两个集合的公共元素组成的集合;并集就是将两集合的元素放在一起组成的集合. 1.已知集合A={2,m},B={3,m2},若A∪B={1,2,3,m},求m的值.
【解析】 由A∪B中含有4个元素可知,m2≠m,
∴m≠0且m≠1,∴m2=1,∴m=-1. 设全集为R,A={x|3≤x<7},B={x|2<x<10},
求?R(A∪B)及(?RA)∩B.【思路点拨】【解析】 把全集R和集合A、B在数轴上表示如下:由图知,A∪B={x|2<x<10},
∴?R(A∪B)={x|x≤2或x≥10}.
∵?RA={x|x<3或x≥7},
∴(?RA)∩B={x|2<x<3或7≤x<10}. (1)数轴与Venn图有同样的直观功效,在数轴上可以直观表示数集,所以进行集合的交、并、补运算时,经常在数轴上进行表示.
(2)交集、并集、补集还有如下关系:
?U(A∩B)=(?UA)∪(?UB),?U(A∪B)=(?UA)∩(?UB).
2.已知全集U={x|x≤5},集合A={x|-2<x<2},B={x|-3<x≤3}.求?UA,A∩B,?U(A∩B),(?UA)∩B. 【思路点拨】 由题目可获取以下主要信息:①全集U,集合A、B均为无限集;②所求问题为集合间交、并、补运算.解答此题可借助数轴求解.
由图可知,
?UA={x|x≤-2或2≤x≤5},
A∩B={x|-2<x<2},
?U(A∩B)={x|x≤-2或2≤x≤4},
(?UA)∩B={x|-3<x≤-2或2≤x≤3}.【解析】 把全集U和集合A,B在数轴上表示如下: 已知全集U={1,2,3,4,5}.A={x|x2-5x+m=0},B={x|x2+nx+12=0},且?UA∪B={1,3,4,5},求m+n的值.
【思路点拨】 A、B是由一元二次方程的根为元素组成的集合,又?UA∪B={1,3,4,5},故2∈A.【解析】 ∵U={1,2,3,4,5},?UA∪B={1,3,4,5},
∴2∈A,又A={x|x2-5x+m=0},
∴2是关于x的方程x2-5x+m=0的一个根,
得m=6且A={2,3},
∴?UA={1,4,5}.而?UA∪B={1,3,4,5},
∴3∈B,又B={x|x2+nx+12=0},
∴3一定是关于x的方程x2+nx+12=0的一个根.
∴n=-7且B={3,4},∴m+n=-1. 正确理解条件?UA∪B={1,3,4,5}是解题的关键,解决此类问题时,可以借助Venn图辅助求解,结合已知条件明确一些元素的具体分布区域.
3.已知集合A={x|x2+ax+12b=0}和B={x|x2-ax+b=0},满足(?UA)∩B={2},A∩(?UB)={4},U=R,求实数a,b的值.
【解析】 ∵(?UA)∩B={2},
∴2∈B,但2?A.
∵A∩(?UB)={4},∴4∈A,但4?B.
∴ ∴a= ,b= . 1.对并集概念的理解
(1)定义中的“x∈A,或x∈B”包含三种情况:“x∈A,但x?B”;“x∈B,但x?A”;“x∈A,且x∈B”.Venn图如图所示.另外,在求两个集合的并集时,它们的公共元素只出现一次.
(2)并集在定义中是由集合A与B的所有元素组成的集合,从这个意义上讲,A∪B可以类比实数的加法运算.2.对交集概念的理解 (1)并不是任何两个集合都有公共元素,当集合A与B没有公共元素时,不能说A与B没有交集,而是A∩B=?.如图所示.
(2)定义中的“所有”两字的含义是,不仅“A∩B中的任意元素都是A与B的公共元素”,同时还有“A与B的公共元素都属于A∩B”. (3)全集含有所要研究的集合的所有元素,因此,全集是对所研究问题而言的相对概念.全集既可以是无限集,也可以是有限集. 3.关于全集与补集
(1)补集与全集是两个密不可分的概念,同一个集合在不同的全集中补集是不同的,不同的集合在同一个全集中的补集也不同.另外全集是一个相对概念.
(2)?UA的数学意义包括两个方面:首先必须具备A?U,其次是运用“元素分析法”定义?UA={x|x∈U,且x?A},补集是集合间的运算关系,这可以和实数的减法相类比.4.补集的性质
根据补集的定义,补集仍是一个集合,显然有以下性质:
(1)?AA=?,?A?=A.
(2)?U(?UA)=A.
(3)A∪?UA=U,A∩?UA=?. 设集合A={x∈R|x2+2x+2-p=0},且A∩{x|x>0}=?,求实数p的取值范围. 【错解】 依题意,方程x2+2x+2-p=0没有实数解,因此Δ=22-4(2-p)<0,解得p<1.所以实数p的取值范围为{p|p<1}.
【错因】 A∩{x|x>0}=?,表示方程x2+2x+2-p=0没有正实数解,此时等价于方程没有实数解或有非正实数解,本题错解中由于没有正确理解这一集合语言,而造成错误.我们在解题时应避免出现这种由于对题意把握不准而造成的错误.【正解】 由题意,若A=?,即Δ=22-4(2-p)<0,所以p<1.进入备考水平测试
