人教b版必修1数学:第1章集合—高效整合
文档属性
| 名称 | 人教b版必修1数学:第1章集合—高效整合 |
|
|
| 格式 | rar | ||
| 文件大小 | 745.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-25 00:00:00 | ||
图片预览






文档简介
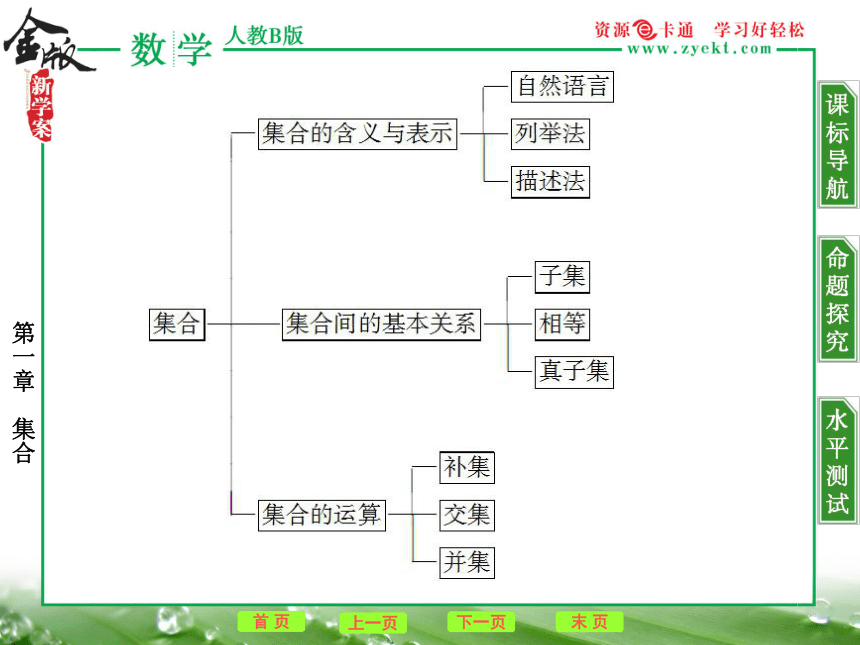
课件18张PPT。 1.集合的含义与表示
(1)通过实例,了解集合的含义,体会元素与集合的“属于”关系.
(2)能选择自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题,感受集合语言的意义和作用.
2.集合间的基本关系
(1)理解集合之间包含与相等的含义,能识别给定集合的子集.
(2)在具体情境中,了解全集与补集的含义. 3.集合的基本运算
(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.
(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集.
(3)能使用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用. 1.以考查集合的运算为主,同时考查集合的性质及集合与元素,集合与集合之间的关系,还注意对“Venn图”的考查.
2.单独考查集合知识以选择题为主,也有填空题出现.与其他主干知识结合也会出现在解答题中.
3.本章是高中数学的起始章节,对函数以及后续学习至关重要,高考中是必考内容,但大都属于低档题. 1.用集合元素的互异性解题
集合元素的互异性,是集合的重要属性,教与学实践告诉我们,集合中元素的互异性常常在解题中忽略,从而导致解题的失败.下面再结合例题进一步讲解,以强化对集合元素互异性的认识. 已知集合A={a,a+b,a+2b},B={a,ac,ac2}.若A=B,求c的值.【解析】 ∵A=B,须分情况讨论.
(1)若a+b=ac,且a+2b=ac2,解得a+ac2-2ac=0.
a=0时,集合B中的三个元素均为零,和元素互异性矛盾,
故a≠0.∴c2-2c+1=0,即c=1.
但c=1时,B中的三元素又相同,故无解.
(2)若a+b=ac2,且a+2b=ac,
消去b得2ac2-ac-a=0.
∵a≠0,∴2c2-c-1=0,即(c-1)(2c+1)=0.
又c≠1,故c= .
综上所述,c= . 2.用空集的特殊性解题
空集是一个特殊的集合,它不含任何元素,是任何集合的子集,是任何非空集合的真子集,在解决集合之间关系问题时,它往往易被忽视而导致解题失误. 已知集合A={x|-2≤x≤5},集合B={x|p+1≤x≤2p-1},若A∩B=B,求实数p的取值范围.【解析】 ∵A∩B=B,∴B?A,
(1)当B=?时,p+1>2p-1,
即p<2,此时满足B?A;
(2)当B≠?时,又B?A,借助数轴表示知
故2≤p≤3.由(1)(2)得p≤3. 3.用数轴分析法解题
对初学者来说,在进行集合的交集、并集、补集运算时,往往由于运算能力差或考虑不全面而极易出错.此时,数轴分析法是个好帮手,能将复杂问题直观化,在具体应用时,要注意端点是实心还是空心,以免增解或漏解.
已知集合A={x|-2<x<4},B={x|x-m<0}.
(1)若A∩B=?,求实数m的取值范围.
(2)若A?B,求实数m的取值范围.【解析】 如图.
(1)由数轴知,若A∩B=?,只有m≤-2.
(2)若A?B,只有m≥4. 1.用数形结合思想解题
数形结合思想,其实质是将抽象的数学语言与直观的图形结合起来,使抽象思维和形象思维结合,通过对图形的认识,数形结合的转化,可以培养思维的灵活性、形象性,使问题化难为易,化抽象为具体.通过“形”往往可以解决用“数”很难解决的问题.集合中常用的方法是数轴法和Venn图法. 已知全集U={x|x2<50,x∈N},L∩(?UM)={1,6},M∩(?UL)={2,3},?U(M∪L)={0,5},求集合M和L. 【解析】 第一步:求得全集U={x|x2<50,x∈N}={0,1,2,3,4,5,6,7};
第二步:将L∩(?UM)={1,6},M∩(?UL)={2,3},?U(M∪L)={0,5}中元素在Venn图中依次定位;
第三步:将元素4,7定位;
第四步:根据图中的元素位置,得集合M={2,3,4,7},集合L={1,4,6,7}. 2.用等价转化思想解题
在解决一些集合问题时,当一种集合的表达形式不好入手时,常将其转化为另一种形式,使问题明朗化,如“A是B的子集”、“A∩B=A”、“A∪B=B”、“A?B”等都是同一含义.另外,集合中数学语言的常见形式主要有三种,即文字语言、符号语言、图形语言,它们可以相互转化,通过合理的转化,往往能简捷迅速地得到解题思路. 已知U={(x,y)|x∈R,y∈R},A={(x,y)|x+y=1},B= ,求(?UB)∩A. 【解析】 集合U={(x,y)|x∈R,y∈R}是平面上所有点的集合;集合A是直线x+y=1上的点的集合;集合B是直线x+y=1上的点的集合,但要除去点(1,0);而?UB表示点(1,0)以及平面上除了直线x+y=1上的所有点以外的点,所以(?UB)∩A对应的元素为(1,0),即(?UB)∩A={(1,0)}. 3.用特殊化思想解题
特殊化思想是一种重要的数学思想,对于许多抽象的集合问题,灵活地取一些符合条件的特殊集合,往往能起到化繁为简、化难为易的功效.另外,特殊值法解选择题是特殊与一般思想在解题中的具体应用,相当于增加题设条件,可使问题简单化. 设集合M= ,
N= ,则( )
A.M=N B.M是N的真子集
C.N是M的真子集 D.M∩N=?
【解析】 由∈N,而?M,排除A,C;又∈N,且∈M,再排除D.
【答案】 B 4.用分类讨论思想解题
解分类讨论问题的实质是将整体问题化为部分来解决,从而增加题设条件,这也是解分类讨论问题的指导思想.当问题中含有参数或问题是分类给出的,常常需要分类讨论.
已知A={x|x2-3x+2=0},B={x|ax-2=0},且A∪B=A,求实数a组成的集合C.【解析】 由x2-3x+2=0得x=1或2,
∴A={1,2},∵A∪B=A,∴B?A.
(1)当B=?时,a=0,此时方程ax-2=0无解,
∴a=0时满足B?A.
(2)当B≠?时,B={x|ax-2=0}= ?{1,2}=A,
∴ =1或 =2,∴a=2或1.
综上,实数a=0,1,2,∴集合C={0,1,2}.进入章末质量评估
(1)通过实例,了解集合的含义,体会元素与集合的“属于”关系.
(2)能选择自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题,感受集合语言的意义和作用.
2.集合间的基本关系
(1)理解集合之间包含与相等的含义,能识别给定集合的子集.
(2)在具体情境中,了解全集与补集的含义. 3.集合的基本运算
(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.
(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集.
(3)能使用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用. 1.以考查集合的运算为主,同时考查集合的性质及集合与元素,集合与集合之间的关系,还注意对“Venn图”的考查.
2.单独考查集合知识以选择题为主,也有填空题出现.与其他主干知识结合也会出现在解答题中.
3.本章是高中数学的起始章节,对函数以及后续学习至关重要,高考中是必考内容,但大都属于低档题. 1.用集合元素的互异性解题
集合元素的互异性,是集合的重要属性,教与学实践告诉我们,集合中元素的互异性常常在解题中忽略,从而导致解题的失败.下面再结合例题进一步讲解,以强化对集合元素互异性的认识. 已知集合A={a,a+b,a+2b},B={a,ac,ac2}.若A=B,求c的值.【解析】 ∵A=B,须分情况讨论.
(1)若a+b=ac,且a+2b=ac2,解得a+ac2-2ac=0.
a=0时,集合B中的三个元素均为零,和元素互异性矛盾,
故a≠0.∴c2-2c+1=0,即c=1.
但c=1时,B中的三元素又相同,故无解.
(2)若a+b=ac2,且a+2b=ac,
消去b得2ac2-ac-a=0.
∵a≠0,∴2c2-c-1=0,即(c-1)(2c+1)=0.
又c≠1,故c= .
综上所述,c= . 2.用空集的特殊性解题
空集是一个特殊的集合,它不含任何元素,是任何集合的子集,是任何非空集合的真子集,在解决集合之间关系问题时,它往往易被忽视而导致解题失误. 已知集合A={x|-2≤x≤5},集合B={x|p+1≤x≤2p-1},若A∩B=B,求实数p的取值范围.【解析】 ∵A∩B=B,∴B?A,
(1)当B=?时,p+1>2p-1,
即p<2,此时满足B?A;
(2)当B≠?时,又B?A,借助数轴表示知
故2≤p≤3.由(1)(2)得p≤3. 3.用数轴分析法解题
对初学者来说,在进行集合的交集、并集、补集运算时,往往由于运算能力差或考虑不全面而极易出错.此时,数轴分析法是个好帮手,能将复杂问题直观化,在具体应用时,要注意端点是实心还是空心,以免增解或漏解.
已知集合A={x|-2<x<4},B={x|x-m<0}.
(1)若A∩B=?,求实数m的取值范围.
(2)若A?B,求实数m的取值范围.【解析】 如图.
(1)由数轴知,若A∩B=?,只有m≤-2.
(2)若A?B,只有m≥4. 1.用数形结合思想解题
数形结合思想,其实质是将抽象的数学语言与直观的图形结合起来,使抽象思维和形象思维结合,通过对图形的认识,数形结合的转化,可以培养思维的灵活性、形象性,使问题化难为易,化抽象为具体.通过“形”往往可以解决用“数”很难解决的问题.集合中常用的方法是数轴法和Venn图法. 已知全集U={x|x2<50,x∈N},L∩(?UM)={1,6},M∩(?UL)={2,3},?U(M∪L)={0,5},求集合M和L. 【解析】 第一步:求得全集U={x|x2<50,x∈N}={0,1,2,3,4,5,6,7};
第二步:将L∩(?UM)={1,6},M∩(?UL)={2,3},?U(M∪L)={0,5}中元素在Venn图中依次定位;
第三步:将元素4,7定位;
第四步:根据图中的元素位置,得集合M={2,3,4,7},集合L={1,4,6,7}. 2.用等价转化思想解题
在解决一些集合问题时,当一种集合的表达形式不好入手时,常将其转化为另一种形式,使问题明朗化,如“A是B的子集”、“A∩B=A”、“A∪B=B”、“A?B”等都是同一含义.另外,集合中数学语言的常见形式主要有三种,即文字语言、符号语言、图形语言,它们可以相互转化,通过合理的转化,往往能简捷迅速地得到解题思路. 已知U={(x,y)|x∈R,y∈R},A={(x,y)|x+y=1},B= ,求(?UB)∩A. 【解析】 集合U={(x,y)|x∈R,y∈R}是平面上所有点的集合;集合A是直线x+y=1上的点的集合;集合B是直线x+y=1上的点的集合,但要除去点(1,0);而?UB表示点(1,0)以及平面上除了直线x+y=1上的所有点以外的点,所以(?UB)∩A对应的元素为(1,0),即(?UB)∩A={(1,0)}. 3.用特殊化思想解题
特殊化思想是一种重要的数学思想,对于许多抽象的集合问题,灵活地取一些符合条件的特殊集合,往往能起到化繁为简、化难为易的功效.另外,特殊值法解选择题是特殊与一般思想在解题中的具体应用,相当于增加题设条件,可使问题简单化. 设集合M= ,
N= ,则( )
A.M=N B.M是N的真子集
C.N是M的真子集 D.M∩N=?
【解析】 由∈N,而?M,排除A,C;又∈N,且∈M,再排除D.
【答案】 B 4.用分类讨论思想解题
解分类讨论问题的实质是将整体问题化为部分来解决,从而增加题设条件,这也是解分类讨论问题的指导思想.当问题中含有参数或问题是分类给出的,常常需要分类讨论.
已知A={x|x2-3x+2=0},B={x|ax-2=0},且A∪B=A,求实数a组成的集合C.【解析】 由x2-3x+2=0得x=1或2,
∴A={1,2},∵A∪B=A,∴B?A.
(1)当B=?时,a=0,此时方程ax-2=0无解,
∴a=0时满足B?A.
(2)当B≠?时,B={x|ax-2=0}= ?{1,2}=A,
∴ =1或 =2,∴a=2或1.
综上,实数a=0,1,2,∴集合C={0,1,2}.进入章末质量评估
