人教b版必修1数学:第2章函数 213函数的单调性
文档属性
| 名称 | 人教b版必修1数学:第2章函数 213函数的单调性 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-25 00:00:00 | ||
图片预览








文档简介
课件25张PPT。2.1.3 函数的单调性初中学习过一次函数、二次函数.还记得函数f(?x)?=x2的图象特征吗?自左向右,图象是 ,即函数值随着x的增大而 . .函数f(?x?)=x2的图象是 ,而且其图象在区间?(-∞,0]内是 ,即函数值随x的增大而 ;在区间?(0,+∞)?内图象是 ,即函数值随x的增大而 .上升的增大拋物线下降的减小上升的增大1.增函数与减函数
一般地,设函数y=f?x?的定义域为A,区间M?A,如果取区间M中的 ,当改变量Δx=x2-x1>0时,
有 ,那么就称函数y=f?(x?)在区间M上是 ;当改变量Δx=x2-x1>0时,有Δy=f?(x2?)-f?(x1?)<0,那么就称函数y=f(?x?)在区间M上是 .
2.单调性与单调区间
如果一个函数在某个区间M上是 或是 就说这个函数在这个区间M上具有单调性,区间M称为 .任意两个值x1、x2Δy=f?(x2?)-f?(x1)?>0增函数减函数增函数减函数单调区间能否将增函数?减函数?定义中的“任意两个值x1,x2”,改为“存在两个值x1,x2”?
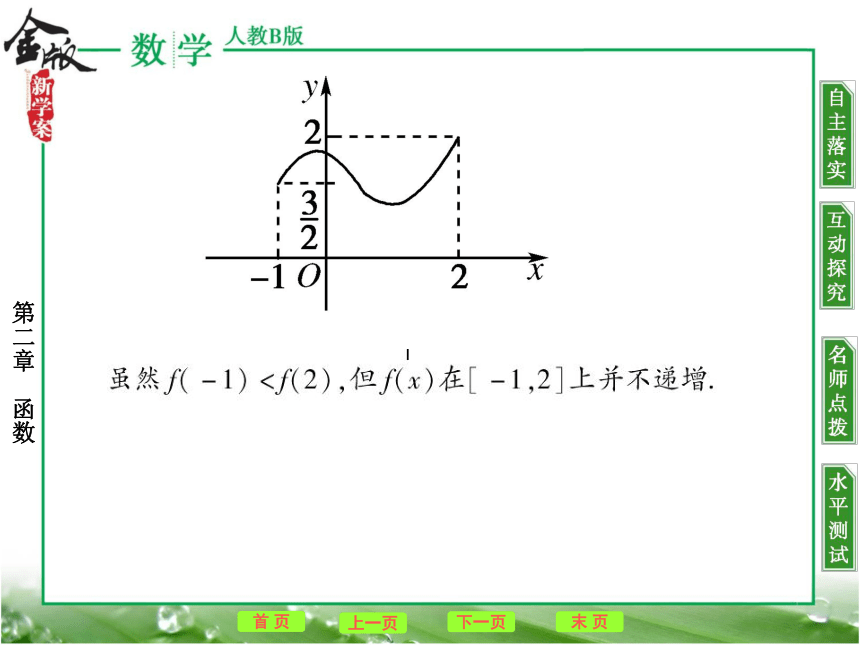
【提示】 不能.如图所示,【思路点拨】 紧扣函数单调性的定义完成证明.根据定义证明函数的单调性可按如下步骤进行:(1)取值.即设x1,x2是该区间内的任意两个值,且x1?(2)作差变形.即作差f?(x1?)-f?(x2?),并通过因式分解、配方、有理化等方法,使其转化为易于判断正负的式子;
?(3)定号.即确定f?(x1?)-f?(x2?)的符号;
?(4)判断.即根据定义得出结论.其中第二步是关键,在变形中一般尽量化为几个最简因式的积或几个完全平方的形式.要通过画图求单调区间,要求图象要相对精确.特别是拐点、端点、交点等必须非常明确,否则必然出错.2.确定函数f?x?=-x2+2|x|+3的单调区间.已知函数f?x?是定义在(?0,+∞?)上的增函数,解不等式f?(2x?)-f?(x-2?)>0.
【思路点拨】 根据定义域和单调性,将原不等式转化为不等式组求解.(1)?当已知函数的单调性及函数值的大小时,可以转化为自变量的大小关系.
?(2)?转化不等式不能忽略定义域.也就是要保证原不等式的各项都有意义.因此,这类问题一般都要化为不等式组求解 3.本题若改为f?(x?)在?(0,+∞?)上为减函数,结果如何?已知函数f(?x)?=x2+2?(a-1?)x+2在区间?(-∞,4]上是减函数,求实数a的取值范围.
【思路点拨】 解答本题可先将函数解析式配方,然后找出图象的对称轴,再考虑对称轴与所给区间的位置关系,利用数形结合求解.(1)?二次函数是常见函数,遇到二次函数后就配方找其对称轴,画出图象,会给研究问题带来很大的方便.
?(2?)已知函数单调性求参数的取值范围,要注意数形结合,采用逆向思维方法.4.本例中,若将函数“在区间(?-∞,4]上是减函数”改为“函数的单调递减区间为?(-∞,4]”,则a为何值?
【解析】 由例题知函数f?(x?)的单调递减区间为(?-∞,1-a],
∴1-a=4,a=-3.1.函数单调性概念中要注意的几点
?(1)?定义中x1、x2的三个特征:一是任意性,即“任意取x1、x2”,“任意”二字绝不能丢掉.证明单调性时更不可随意以两个特殊值替换.例如:对于函数y=x2来说,令x1=-1,x2=2,有x1<x2,且Δx=x2-x1>0,Δy=y2-y1=x22-x12=4-1=3>0,但不能说该函数是单调递增的;二是有大小,通常规定x1?(3)函数的单调性是对于函数定义域内的某个子区间而言的,可以说是函数的“局部”性质.有些函数在整个定义域内可能是单调的,如一次函数y=kx+b?(k≠0?);有些函数在定义域内的部分区间上是增函数,而在另一部分区间上可能是减函数,如二次函数y=x2,在[0,+∞)上是增函数,而在?(-∞,0?)上则是减函数;还有的函数在某一区间上是非单调的,如函数y=x2在[-1,2]上没有单调性.若一个函数是由多个简单函数复合而成的,则看简单函数中减函数的个数.若减函数有偶数个,则复合而成的函数为增函数;若减函数有奇数个,则复合而成的函数为减函数.【错因】 出现上述错误解法的原因主要为不清楚抽象函数的定义域,在抽象函数中满足函数关系式的自变量首先应在定义域内,这是一个极易被忽视也是极易出现错误的地方,也就是说变量x首先应满足-1≤x-2≤1,-1≤1-x≤1,在此基础上利用单调性的定义将“ f ”符号脱掉.课时作业
点击进入链接
一般地,设函数y=f?x?的定义域为A,区间M?A,如果取区间M中的 ,当改变量Δx=x2-x1>0时,
有 ,那么就称函数y=f?(x?)在区间M上是 ;当改变量Δx=x2-x1>0时,有Δy=f?(x2?)-f?(x1?)<0,那么就称函数y=f(?x?)在区间M上是 .
2.单调性与单调区间
如果一个函数在某个区间M上是 或是 就说这个函数在这个区间M上具有单调性,区间M称为 .任意两个值x1、x2Δy=f?(x2?)-f?(x1)?>0增函数减函数增函数减函数单调区间能否将增函数?减函数?定义中的“任意两个值x1,x2”,改为“存在两个值x1,x2”?
【提示】 不能.如图所示,【思路点拨】 紧扣函数单调性的定义完成证明.根据定义证明函数的单调性可按如下步骤进行:(1)取值.即设x1,x2是该区间内的任意两个值,且x1
?(3)定号.即确定f?(x1?)-f?(x2?)的符号;
?(4)判断.即根据定义得出结论.其中第二步是关键,在变形中一般尽量化为几个最简因式的积或几个完全平方的形式.要通过画图求单调区间,要求图象要相对精确.特别是拐点、端点、交点等必须非常明确,否则必然出错.2.确定函数f?x?=-x2+2|x|+3的单调区间.已知函数f?x?是定义在(?0,+∞?)上的增函数,解不等式f?(2x?)-f?(x-2?)>0.
【思路点拨】 根据定义域和单调性,将原不等式转化为不等式组求解.(1)?当已知函数的单调性及函数值的大小时,可以转化为自变量的大小关系.
?(2)?转化不等式不能忽略定义域.也就是要保证原不等式的各项都有意义.因此,这类问题一般都要化为不等式组求解 3.本题若改为f?(x?)在?(0,+∞?)上为减函数,结果如何?已知函数f(?x)?=x2+2?(a-1?)x+2在区间?(-∞,4]上是减函数,求实数a的取值范围.
【思路点拨】 解答本题可先将函数解析式配方,然后找出图象的对称轴,再考虑对称轴与所给区间的位置关系,利用数形结合求解.(1)?二次函数是常见函数,遇到二次函数后就配方找其对称轴,画出图象,会给研究问题带来很大的方便.
?(2?)已知函数单调性求参数的取值范围,要注意数形结合,采用逆向思维方法.4.本例中,若将函数“在区间(?-∞,4]上是减函数”改为“函数的单调递减区间为?(-∞,4]”,则a为何值?
【解析】 由例题知函数f?(x?)的单调递减区间为(?-∞,1-a],
∴1-a=4,a=-3.1.函数单调性概念中要注意的几点
?(1)?定义中x1、x2的三个特征:一是任意性,即“任意取x1、x2”,“任意”二字绝不能丢掉.证明单调性时更不可随意以两个特殊值替换.例如:对于函数y=x2来说,令x1=-1,x2=2,有x1<x2,且Δx=x2-x1>0,Δy=y2-y1=x22-x12=4-1=3>0,但不能说该函数是单调递增的;二是有大小,通常规定x1
点击进入链接
