人教b版必修1数学:第2章函数 214函数的奇偶性
文档属性
| 名称 | 人教b版必修1数学:第2章函数 214函数的奇偶性 |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-25 19:30:00 | ||
图片预览








文档简介
课件22张PPT。2.1.4 函数的奇偶性1.奇偶函数的定义
设函数y=f?(x?)的定义域为D,如果对D内的 ,都有 ,且f?(-x?)= ?,则这个函数叫做 .
设函数y=g?(x)?的定义域为D,如果对于D内的任意一个x,都有 ,且 ,则这个函数叫做 .
2.奇偶函数的图象
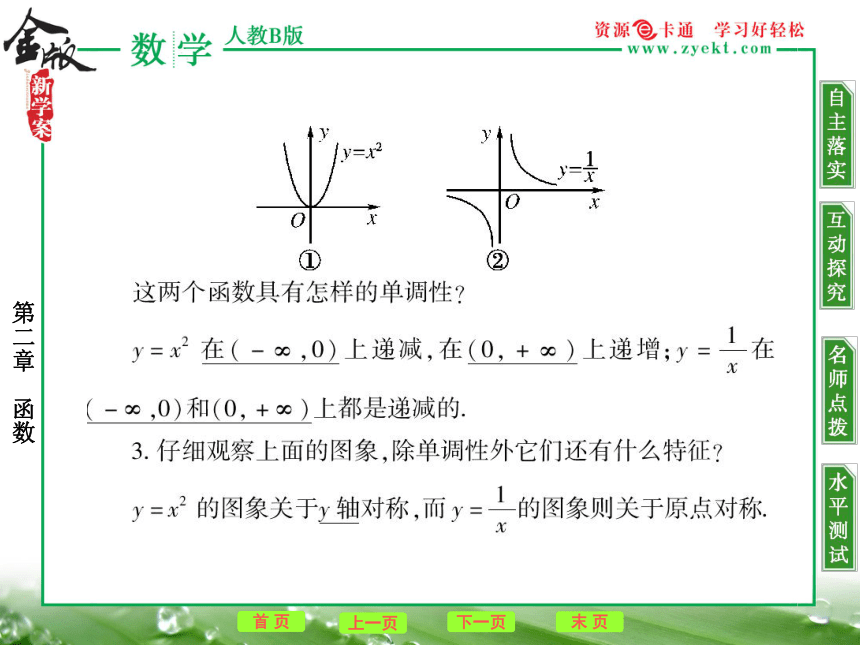
如果一个函数是奇函数,则这个函数的图象是以 .为对称中心的中心对称图形,反之,如果一个函数的图象是以坐标原点为对称中心的中心对称图形,则这个函数是 .
如果一个函数是偶函数,则它的图象是以 为对称轴的轴对称图形,反之,如果一个函数的图象关于y轴对称,则这个函数是 .任意一个x-x∈D-f(?x)奇函数-x∈Dg?(-x?)=g?(x?)偶函数坐标原点奇函数y轴偶函数1.若奇函数f?(x?)在x=0处有定义,则f(?0?)等于什么?
【提示】 由奇函数定义知,f?(-0?)=-f(?0?),故f(?0)?=0
2.有没有既是奇函数又是偶函数的函数?
【提示】 有,f(?x?)=0,x∈(?-a,a)(??a>0?)既是奇函数又是偶函数.判断下列函数的奇偶性:【思路点拨】 先确定函数的定义域是否关于原点对称,再在定义域内化简函数式,然后用定义判断.判断函数的奇偶性,一般用以下两种方法:(2)?图象法:若函数图象关于原点对称,则函数为奇函数;若函数图象关于y轴对称,则函数为偶函数.1.判断下列函数的奇偶性,并说明理由:已知f?(x?)是R上的奇函数,当x∈?(-∞,0?)时,根据奇偶性的定义,由函数f(?x)?在原点一侧某一区间上的解析式必能求在原点另一侧与之对应的区间上的解析式.对于奇函数有f(?x?)=-f?(-x?),对于偶函数有f?(x)?=f(?-x)?.2.已知f?x?为奇函数,并且在?(-∞,0]上为减函数,试判断f?x?在[0,+∞?)上的单调性.设定义在[-2,2]上的奇函数f?(x?)在区间[0,2]上单调递减,若f?(m?)+f(?m-1?)>0,求实数m的取值范围.解决此类问题时一定要充分利用已知的条件,把已知不等式转化成f?(x1?)>f?(x2?)或f(?x1)?<f?(x2?)的形式,再根据奇函数在对称区间上单调性一致,偶函数的单调性相反,列出不等式或不等式组,同时不能漏掉函数自身定义域对参数的影响.3.设定义在[-2,2]上的偶函数f?(x)?,当x≥0时,f(?x?)单调递减,若f?(1-m?)<f(?m)?成立,求m的取值范围.
【解析】 ∵f?x?是定义在[-2,2]上的偶函数,1.函数奇偶性的判断
判断函数的奇偶性,一般有以下几种方法:(2)?图象法:奇?偶?函数的充要条件是它的图象关于原点?或y轴?对称.
?(3)性质法:偶函数的和、差、积、商?分母不为零?仍为偶函数;奇函数的和、差仍为奇函数;奇?偶?数个奇函数的积、商?分母不为零?为奇?偶?函数;一个奇函数与一个偶函数的积为奇函数.
2.函数的奇偶性与单调性间的关系
一般地,若f(?x?)为奇函数,则f(?x?)在[a,b]和[-b,-a]上具有相同的单调性;若f(?x?)是偶函数,则f?x?在[a,b]和[-b,-a]上具有相反的单调性.课时作业
点击进入链接
设函数y=f?(x?)的定义域为D,如果对D内的 ,都有 ,且f?(-x?)= ?,则这个函数叫做 .
设函数y=g?(x)?的定义域为D,如果对于D内的任意一个x,都有 ,且 ,则这个函数叫做 .
2.奇偶函数的图象
如果一个函数是奇函数,则这个函数的图象是以 .为对称中心的中心对称图形,反之,如果一个函数的图象是以坐标原点为对称中心的中心对称图形,则这个函数是 .
如果一个函数是偶函数,则它的图象是以 为对称轴的轴对称图形,反之,如果一个函数的图象关于y轴对称,则这个函数是 .任意一个x-x∈D-f(?x)奇函数-x∈Dg?(-x?)=g?(x?)偶函数坐标原点奇函数y轴偶函数1.若奇函数f?(x?)在x=0处有定义,则f(?0?)等于什么?
【提示】 由奇函数定义知,f?(-0?)=-f(?0?),故f(?0)?=0
2.有没有既是奇函数又是偶函数的函数?
【提示】 有,f(?x?)=0,x∈(?-a,a)(??a>0?)既是奇函数又是偶函数.判断下列函数的奇偶性:【思路点拨】 先确定函数的定义域是否关于原点对称,再在定义域内化简函数式,然后用定义判断.判断函数的奇偶性,一般用以下两种方法:(2)?图象法:若函数图象关于原点对称,则函数为奇函数;若函数图象关于y轴对称,则函数为偶函数.1.判断下列函数的奇偶性,并说明理由:已知f?(x?)是R上的奇函数,当x∈?(-∞,0?)时,根据奇偶性的定义,由函数f(?x)?在原点一侧某一区间上的解析式必能求在原点另一侧与之对应的区间上的解析式.对于奇函数有f(?x?)=-f?(-x?),对于偶函数有f?(x)?=f(?-x)?.2.已知f?x?为奇函数,并且在?(-∞,0]上为减函数,试判断f?x?在[0,+∞?)上的单调性.设定义在[-2,2]上的奇函数f?(x?)在区间[0,2]上单调递减,若f?(m?)+f(?m-1?)>0,求实数m的取值范围.解决此类问题时一定要充分利用已知的条件,把已知不等式转化成f?(x1?)>f?(x2?)或f(?x1)?<f?(x2?)的形式,再根据奇函数在对称区间上单调性一致,偶函数的单调性相反,列出不等式或不等式组,同时不能漏掉函数自身定义域对参数的影响.3.设定义在[-2,2]上的偶函数f?(x)?,当x≥0时,f(?x?)单调递减,若f?(1-m?)<f(?m)?成立,求m的取值范围.
【解析】 ∵f?x?是定义在[-2,2]上的偶函数,1.函数奇偶性的判断
判断函数的奇偶性,一般有以下几种方法:(2)?图象法:奇?偶?函数的充要条件是它的图象关于原点?或y轴?对称.
?(3)性质法:偶函数的和、差、积、商?分母不为零?仍为偶函数;奇函数的和、差仍为奇函数;奇?偶?数个奇函数的积、商?分母不为零?为奇?偶?函数;一个奇函数与一个偶函数的积为奇函数.
2.函数的奇偶性与单调性间的关系
一般地,若f(?x?)为奇函数,则f(?x?)在[a,b]和[-b,-a]上具有相同的单调性;若f(?x?)是偶函数,则f?x?在[a,b]和[-b,-a]上具有相反的单调性.课时作业
点击进入链接
