人教b版必修1数学:第2章函数 241函数的零点
文档属性
| 名称 | 人教b版必修1数学:第2章函数 241函数的零点 |  | |
| 格式 | rar | ||
| 文件大小 | 615.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-25 19:30:00 | ||
图片预览






文档简介
课件18张PPT。2.4 函数与方程2.4.1 函数的零点1.方程x2-2x-3=0的根为 ;函数y=x2-2x-3与x轴的
交点为
2.函数y=2x2-8x+1的对称轴为 ,顶点坐标为 .3,-1(3,0),(-1,0).x=2(2,-7)1.函数的零点
(1)一般地,如果函数y=f(x) ,即 ,
则a叫做这个函数的零点.
(2)有时也把一个函数的 的公共点,叫做这个函数的零点.
2.二次函数零点的性质
(1)当函数的图象通过零点且穿过x轴时,函数值
(2)两个零点把x轴分为 区间,在每个区间上所有函数值
保持 在实数a处的值等于零f(a)=0图象与x轴变号.三个同号.3.零点存在定理
零点存在定理:如果函数y=f(x)在区间[a,b]上的图象是
的曲线,并且有 ,那么,函数y=f(x)在区间(a,b)
内至少有一个零点,即存在x0∈(a,b),使 ,这个x0也就是
方程f(x)=0的根.连续不断f(a)·f(b)<0f(x0)=0函数的零点就是点,任何函数都有零点,对吗?【提示】 不对.函数的零点不是点,而是函数y=f(x)与x轴交点
的横坐标,即零点是一个实数,当函数的自变量取这个实数时其函
数值为零.函数f(x)= 无零点,因为方程 =0无实根,因此,
并非所有的函数都有零点.对于函数f(x)=x2+mx+n,若f(a)>0,f(b)>0,则函数f(x)在
区间(a,b)内( )
A.一定有零点 B.一定没有零点
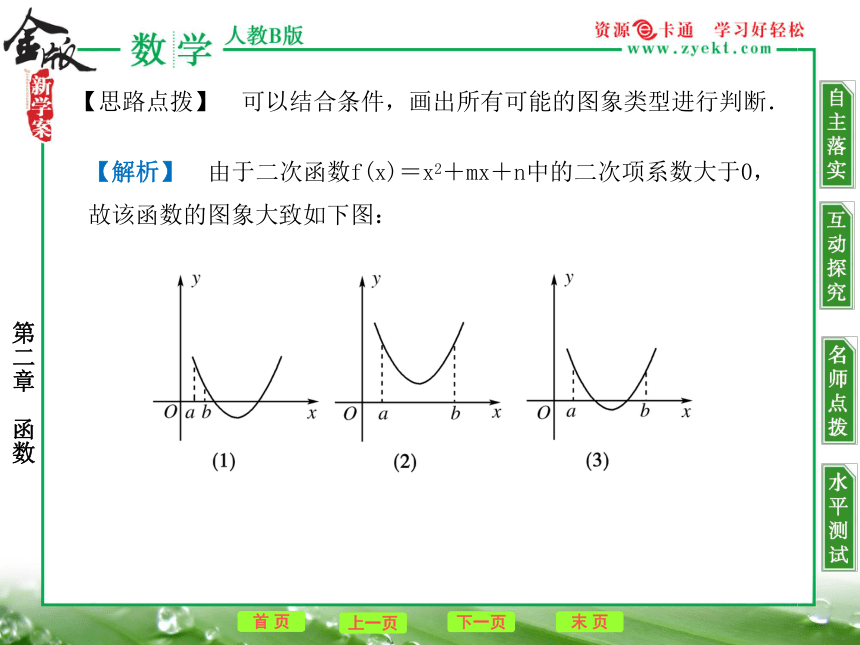
C.可能有两个零点 D.至多有一个零点【思路点拨】 可以结合条件,画出所有可能的图象类型进行判断.【解析】 由于二次函数f(x)=x2+mx+n中的二次项系数大于0,
故该函数的图象大致如下图:若如图(1),可知B错;结合图(2)(3)可知A、D都错.
【答案】 C判断函数零点通常有两种方法,一是求方程的根;二是画图象,
本题通过图象判断清晰明了.1.二次函数y=ax2+bx+c(a≠0)中,ac<0,则函数的零点
个数是( )
A.1 B.2
C.0 D.无法确定【解析】 解法一:因为c=f(0),所以ac=a·f(0)<0,
即a与f(0)异号,即 所以函数必有两个零点.
解法二:可由二次方程的判别式得到Δ=b2-4ac.又因为ac<0,
所以Δ>0.此方程有两个不相等的实根.
【答案】 B求函数y=x3-2x2-x+2的零点,并画出图象.
【思路点拨】 函数的零点就是方程的实根,各实根(函数的零点)
将定义域划分为若干个区间,由零点的性质便可确定函数f(x)在各
个区间上的符号,从而可大致画出函数的图象. 令f(x)=x3-2x2-x+2=0,
则有x2(x-2)-(x-2)=(x+1)(x-1)(x-2)=0,
∴函数f(x)的零点为-1、1、2.
又f(0)=2>0,根据函数零点的两个性质可知在区间(-1,1)内,
f(x)>0;在区间(-∞,-1)内,f(x)<0;在区间(1,2)内,
f(x)<0;在区间(2,+∞)内,f(x)>0.其图象如下图所示:本题先通过解方程求出函数的零点,再结合零点的性质分析函数在
各区间内的符号,从而画出函数的大致图象.体现了函数的零点,
相应方程的根以及函数图象间的密切关系.2.求y=-x2-2x+3的零点,并分别指出y>0,y<0时x的取值范围.
【解析】 解一元二次方程-x2-2x+3=0,
得x1=-3,x2=1,
∴函数y=-x2-2x+3的零点是-3,1.
函数简图如图所示,从图象可知,当-3<x<1时,y>0;
当x<-3或x>1时,y<0.∴y>0时,x的取值范围是(-3,1);y<0时,x的取值范围
是(-∞,-3)∪(1,+∞).已知函数f(x)=x2-x+a至少有一个零点为非负实数,求实数a的
取值范围.
【思路点拨】 关于x的方程x2-x+a=0至少有一个非负实数根,
可分为方程有“两正根、一正根一负根、一根为0另一根为正(负)
根”四种情况,若一一讨论较繁琐,因此可考虑问题的反面.
【解析】 函数f(x)=x2-x+a至少有一个零点为非负实数等价于
方程x2-x+a=0至少有一个非负实根,可以考虑问题的反面,方程
无非负实数根,即方程有两个负实根或无实数根的情况.函数f(x)=x2-x+a图象的对称轴为x= ,
∴方程x2-x+a=0不可能有两个负实根,
∴当方程x2-x+a=0无实根时,Δ=1-4a<0,
∴a>.
即满足题意的实数a的取值范围是.(1)讨论二次函数零点情况,通常转化为讨论一元二次方程的根的
分布问题可以利用求根公式或利用因式分解求出根再加限制,或
结合韦达定理,利用数形结合作转化.
(2)有些问题正面处理复杂而其反面较简单时,常利用“正难则反”和补集的思想来解决.3.已知函数f(x)=x3-4x,
(1)求函数的零点并画函数的图象;
(2)解不等式xf(x)<0.
【解析】 (1)因为x3-4x=x(x-2)(x+2),所以函数的零点
为0,-2,2.3个零点把轴分成4个区间:
(-∞,-2],(-2,0],(0,2],(2,+∞),f(-3)=-15,
f(-1)=3,f(1)=-3,f(3)=15,
由于相邻两个零点之间的所有函数值保持同号,函数的图象
如右图所示.1.函数零点、方程的根、函数图象与x轴的交点
函数y=f(x)的零点就是方程f(x)=0的实数根,也就是函数y=f(x)
的图象与x轴交点的横坐标.方程实根的存在与否,完全等同于函数
零点的存在与否,因此,求方程的根,就是寻找函数的零点,也就
是寻找函数图象与x轴的交点横坐标.
对于不能用公式或因式分解的方法求方程f(x)=0的根的情况,我们
可以将它与函数y=f(x)联系起来,利用函数的性质找出零点,从而
找出方程的根或根所在的区间.2.函数零点存在性的判定方法
(1)利用解方程.函数y=f(x)的零点,可通过解方程f(x)=0作判断.
如函数y=ax2+bx+c(a≠0)的零点,利用判别式Δ=b2-4ac确定方
程ax2+bx+c=0的根的情况即可解决.(2)画出函数的图象,利用函数的性质,确定图象与x轴的交点情况.
如基本初等函数的零点可用图象法作判断.
(3)利用重要结论——零点存在性定理.
判断函数y=f(x)零点的存在性的两个条件:
(1)函数的图象在区间[a,b]上是一条连续不断的曲线.
(2)由f(a)·f(b)<0就可判断函数y=f(x)在区间(a,b)内至少有
一个零点.
注意:①并非函数所有的零点都能用这种方法找到.如y=x2的零
点在x=0附近就没有这样的区间.只有函数值在零点的左右两侧
异号时才能用这种方法.
②利用上述结论只能判断函数y=f(x)在区间(a,b)上零点的存在
性,但不能确定其零点的个数.③若函数有多个零点,则在两个相邻零点间的所有函数值的符号相同.
④上述定理中的条件应同时满足,若缺少其中一条则函数y=f(x)在
区间(a,b)内都未必存在零点.已知二次函数f(x)=x2-(m-1)x+2m在[0,1]上有且只有一个零点,
求实数m的取值范围.
【错解】 由函数零点的性质,得:
f(0)·f(1)<0,得2m(m+2)<0? -2<m<0.
所以实数m的取值范围为(-2,0).
【错因】 错解的原因是只注意到了函数零点性质的应用,而忽略
了问题的其他形式.(1)在[0,1]上有二重零点.(2)端点可能为零点.【正解】 (1)当方程x2-(m-1)x+2m=0在[0,1]上有两个相等实
根时,则 此时m无解.
(2)当方程x2-(m-1)x+2m=0有两个不相等的实根时.
①有且只有一根在[0,1]上时,有f(0)·f(1)<0.
即2m(m+2)<0,得-2<m<0.
②当f(0)=0时,m=0,方程化为x2+x=0.根为x1=0,x2=-1
满足题意.
③当f(1)=0时,m=-2,方程可化为x2+3x-4=0.根为x1=1,
x2=-4,满足题意.
综上所述,实数m的取值范围为[-2,0].课时作业
点击进入链接
交点为
2.函数y=2x2-8x+1的对称轴为 ,顶点坐标为 .3,-1(3,0),(-1,0).x=2(2,-7)1.函数的零点
(1)一般地,如果函数y=f(x) ,即 ,
则a叫做这个函数的零点.
(2)有时也把一个函数的 的公共点,叫做这个函数的零点.
2.二次函数零点的性质
(1)当函数的图象通过零点且穿过x轴时,函数值
(2)两个零点把x轴分为 区间,在每个区间上所有函数值
保持 在实数a处的值等于零f(a)=0图象与x轴变号.三个同号.3.零点存在定理
零点存在定理:如果函数y=f(x)在区间[a,b]上的图象是
的曲线,并且有 ,那么,函数y=f(x)在区间(a,b)
内至少有一个零点,即存在x0∈(a,b),使 ,这个x0也就是
方程f(x)=0的根.连续不断f(a)·f(b)<0f(x0)=0函数的零点就是点,任何函数都有零点,对吗?【提示】 不对.函数的零点不是点,而是函数y=f(x)与x轴交点
的横坐标,即零点是一个实数,当函数的自变量取这个实数时其函
数值为零.函数f(x)= 无零点,因为方程 =0无实根,因此,
并非所有的函数都有零点.对于函数f(x)=x2+mx+n,若f(a)>0,f(b)>0,则函数f(x)在
区间(a,b)内( )
A.一定有零点 B.一定没有零点
C.可能有两个零点 D.至多有一个零点【思路点拨】 可以结合条件,画出所有可能的图象类型进行判断.【解析】 由于二次函数f(x)=x2+mx+n中的二次项系数大于0,
故该函数的图象大致如下图:若如图(1),可知B错;结合图(2)(3)可知A、D都错.
【答案】 C判断函数零点通常有两种方法,一是求方程的根;二是画图象,
本题通过图象判断清晰明了.1.二次函数y=ax2+bx+c(a≠0)中,ac<0,则函数的零点
个数是( )
A.1 B.2
C.0 D.无法确定【解析】 解法一:因为c=f(0),所以ac=a·f(0)<0,
即a与f(0)异号,即 所以函数必有两个零点.
解法二:可由二次方程的判别式得到Δ=b2-4ac.又因为ac<0,
所以Δ>0.此方程有两个不相等的实根.
【答案】 B求函数y=x3-2x2-x+2的零点,并画出图象.
【思路点拨】 函数的零点就是方程的实根,各实根(函数的零点)
将定义域划分为若干个区间,由零点的性质便可确定函数f(x)在各
个区间上的符号,从而可大致画出函数的图象. 令f(x)=x3-2x2-x+2=0,
则有x2(x-2)-(x-2)=(x+1)(x-1)(x-2)=0,
∴函数f(x)的零点为-1、1、2.
又f(0)=2>0,根据函数零点的两个性质可知在区间(-1,1)内,
f(x)>0;在区间(-∞,-1)内,f(x)<0;在区间(1,2)内,
f(x)<0;在区间(2,+∞)内,f(x)>0.其图象如下图所示:本题先通过解方程求出函数的零点,再结合零点的性质分析函数在
各区间内的符号,从而画出函数的大致图象.体现了函数的零点,
相应方程的根以及函数图象间的密切关系.2.求y=-x2-2x+3的零点,并分别指出y>0,y<0时x的取值范围.
【解析】 解一元二次方程-x2-2x+3=0,
得x1=-3,x2=1,
∴函数y=-x2-2x+3的零点是-3,1.
函数简图如图所示,从图象可知,当-3<x<1时,y>0;
当x<-3或x>1时,y<0.∴y>0时,x的取值范围是(-3,1);y<0时,x的取值范围
是(-∞,-3)∪(1,+∞).已知函数f(x)=x2-x+a至少有一个零点为非负实数,求实数a的
取值范围.
【思路点拨】 关于x的方程x2-x+a=0至少有一个非负实数根,
可分为方程有“两正根、一正根一负根、一根为0另一根为正(负)
根”四种情况,若一一讨论较繁琐,因此可考虑问题的反面.
【解析】 函数f(x)=x2-x+a至少有一个零点为非负实数等价于
方程x2-x+a=0至少有一个非负实根,可以考虑问题的反面,方程
无非负实数根,即方程有两个负实根或无实数根的情况.函数f(x)=x2-x+a图象的对称轴为x= ,
∴方程x2-x+a=0不可能有两个负实根,
∴当方程x2-x+a=0无实根时,Δ=1-4a<0,
∴a>.
即满足题意的实数a的取值范围是.(1)讨论二次函数零点情况,通常转化为讨论一元二次方程的根的
分布问题可以利用求根公式或利用因式分解求出根再加限制,或
结合韦达定理,利用数形结合作转化.
(2)有些问题正面处理复杂而其反面较简单时,常利用“正难则反”和补集的思想来解决.3.已知函数f(x)=x3-4x,
(1)求函数的零点并画函数的图象;
(2)解不等式xf(x)<0.
【解析】 (1)因为x3-4x=x(x-2)(x+2),所以函数的零点
为0,-2,2.3个零点把轴分成4个区间:
(-∞,-2],(-2,0],(0,2],(2,+∞),f(-3)=-15,
f(-1)=3,f(1)=-3,f(3)=15,
由于相邻两个零点之间的所有函数值保持同号,函数的图象
如右图所示.1.函数零点、方程的根、函数图象与x轴的交点
函数y=f(x)的零点就是方程f(x)=0的实数根,也就是函数y=f(x)
的图象与x轴交点的横坐标.方程实根的存在与否,完全等同于函数
零点的存在与否,因此,求方程的根,就是寻找函数的零点,也就
是寻找函数图象与x轴的交点横坐标.
对于不能用公式或因式分解的方法求方程f(x)=0的根的情况,我们
可以将它与函数y=f(x)联系起来,利用函数的性质找出零点,从而
找出方程的根或根所在的区间.2.函数零点存在性的判定方法
(1)利用解方程.函数y=f(x)的零点,可通过解方程f(x)=0作判断.
如函数y=ax2+bx+c(a≠0)的零点,利用判别式Δ=b2-4ac确定方
程ax2+bx+c=0的根的情况即可解决.(2)画出函数的图象,利用函数的性质,确定图象与x轴的交点情况.
如基本初等函数的零点可用图象法作判断.
(3)利用重要结论——零点存在性定理.
判断函数y=f(x)零点的存在性的两个条件:
(1)函数的图象在区间[a,b]上是一条连续不断的曲线.
(2)由f(a)·f(b)<0就可判断函数y=f(x)在区间(a,b)内至少有
一个零点.
注意:①并非函数所有的零点都能用这种方法找到.如y=x2的零
点在x=0附近就没有这样的区间.只有函数值在零点的左右两侧
异号时才能用这种方法.
②利用上述结论只能判断函数y=f(x)在区间(a,b)上零点的存在
性,但不能确定其零点的个数.③若函数有多个零点,则在两个相邻零点间的所有函数值的符号相同.
④上述定理中的条件应同时满足,若缺少其中一条则函数y=f(x)在
区间(a,b)内都未必存在零点.已知二次函数f(x)=x2-(m-1)x+2m在[0,1]上有且只有一个零点,
求实数m的取值范围.
【错解】 由函数零点的性质,得:
f(0)·f(1)<0,得2m(m+2)<0? -2<m<0.
所以实数m的取值范围为(-2,0).
【错因】 错解的原因是只注意到了函数零点性质的应用,而忽略
了问题的其他形式.(1)在[0,1]上有二重零点.(2)端点可能为零点.【正解】 (1)当方程x2-(m-1)x+2m=0在[0,1]上有两个相等实
根时,则 此时m无解.
(2)当方程x2-(m-1)x+2m=0有两个不相等的实根时.
①有且只有一根在[0,1]上时,有f(0)·f(1)<0.
即2m(m+2)<0,得-2<m<0.
②当f(0)=0时,m=0,方程化为x2+x=0.根为x1=0,x2=-1
满足题意.
③当f(1)=0时,m=-2,方程可化为x2+3x-4=0.根为x1=1,
x2=-4,满足题意.
综上所述,实数m的取值范围为[-2,0].课时作业
点击进入链接
