等腰三角形
图片预览






文档简介
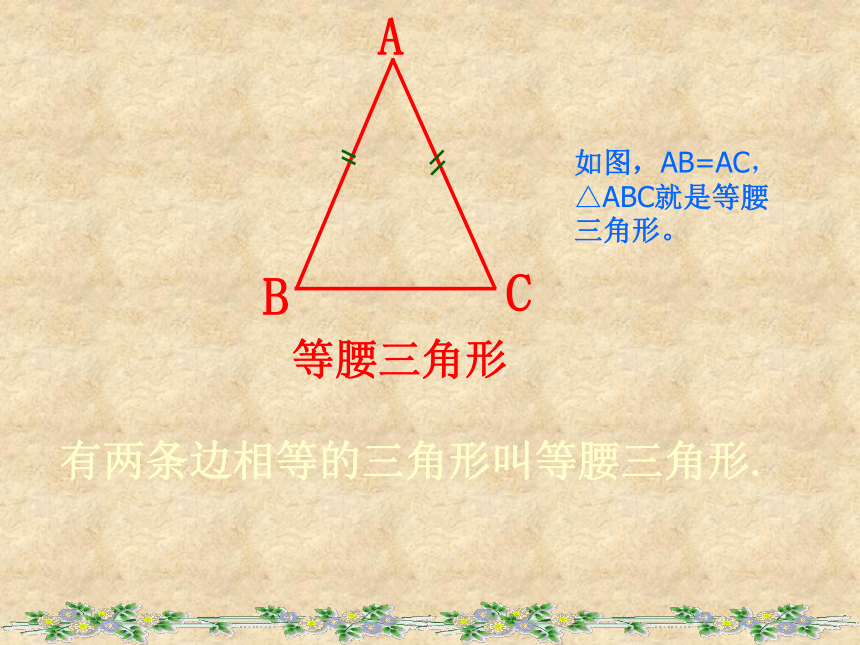
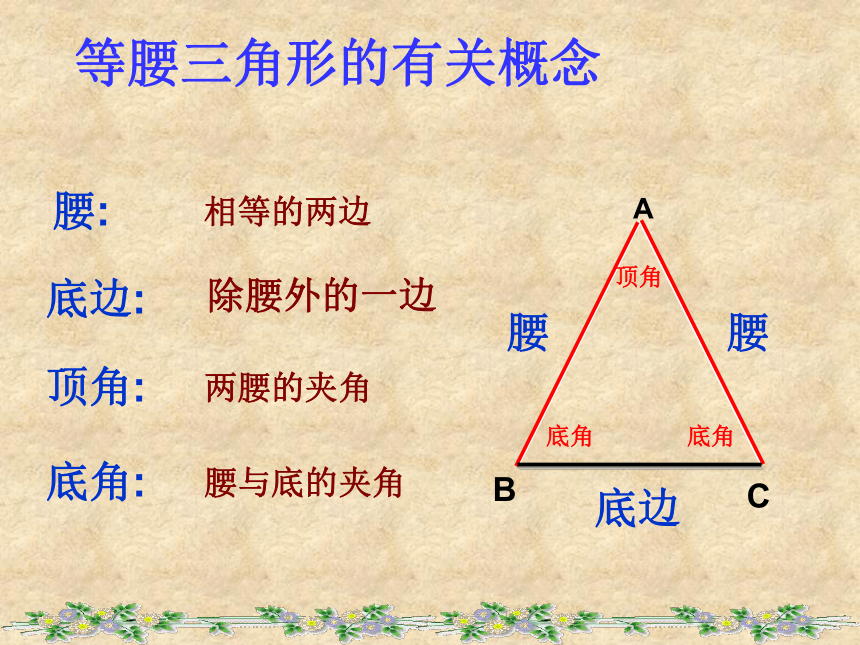
课件25张PPT。天安门城楼西安半坡博物馆石景山体育馆(摔跤)赛场下载图片 等腰三角形等腰三角形你知道什么是等腰三角形吗?有两条边相等的三角形叫等腰三角形.ABC如图,AB=AC,△ABC就是等腰三角形。等腰三角形等腰三角形的有关概念腰腰底边底角底角顶角BC腰:底边:顶角:底角: 相等的两边除腰外的一边两腰的夹角腰与底的夹角A 做一做请同学们观察下面的操作,你能发现什么现象呢?D设问:你发现了什么现象, 猜一猜猜想等腰△ABC有哪些性质? 角: ① ∠B = ∠C
② ∠BAD=∠CDA
③∠ADC= ∠ADB=900
边: ④BD = CD → 两个底角相等
→ AD为顶角∠BAC的平分线
→ AD为底边BC上的高
→ AD为底边BC上的中线
结论: 等腰三角形是轴对称图形;
等腰三角形性质
性质1 等腰三角形的两个底角相等(简写成“等边对等角”);
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。(可简记为“三线合一”)对称轴是顶角平分线(底边上的中线、底边上的高线)所在直线。 等腰三角形性质
性质1 等腰三角形的两个底角相等(简
写成“等边对等角”);
性质2 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合。
(可简记为“三线合一”)数学语言性质1: 在△ABC中, ∵ AB=AC ∴ ∠ABC=?ACB
性质2: ( 1 ) ∵ AB=AC AD是角平分线,
∴ ⊥ , ____=_____ ;
( 2 ) ∵ AB=AC AD是中线,
∴ ⊥ ,∴∠ = ∠____;
( 3 ) ∵ AB=AC AD⊥BC,
∴∠_____=∠______,_____=______ 。
BAD CADBAD CAD
AD BCAD BCBD CDBD CD已知: ΔABC中,AB=AC等腰三角形的性质JG继续DZ 求证:(1)∠B=∠C
在△ABC中,若AB=AC,则∠ABC=?ACB.等腰三角形的性质证明:①作底边BC的中线AD.
思维展示AABCDD证明:作顶角的平分线AD即∠BAD=∠CAD
在△ABD和△ACD中
AB=AC
∠BAD=∠CAD
AD=AD
∴ △ABD≌ △ACD (SAS)
∴ ∠B= ∠C (全等三角形对应角相等)
作AD垂直BC于D。D已知:如图,在ΔABC中,AB=AC
求证:∠B=∠C
证明:即∠BAD=∠CAD=900
在Rt △BAD与 Rt △CAD 中∵AB=AC AD=AD
∴ Rt △BAD≌ Rt △CAD (HL)
D作△ABC的中线AD,交底边BC于D。 D┌作△ABC的高AD,垂直底边BC于D。D12作顶角的平分线AD.AABDCBDC等腰三角形常见辅助线归纳总结归纳总结 等腰三角形性质
性质2 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合。
(可简记为“三线合一”)性质2:在△ABC中, ( 1 ) ∵ AB=AC AD是角平分线,
∴ ⊥ , ____=_____ ;
( 2 ) ∵ AB=AC AD是中线,
∴ ⊥ ,∴∠ = ∠____;
( 3 ) ∵ AB=AC AD⊥BC,
∴∠_____=∠______,_____=______ 。
BAD CADBAD CAD
AD BCAD BCBD CDBD CD数学语言 学以致用——从理论到实践巩固练习一1、已知等腰三角形的两边长分别是4和6,则它的周长是( )
A、14 B、15 C、16 D、14或16
2、若把此等腰三角形的两边长改为3和7,则它的周长应是多少?
结论:在等腰三角形中,注意对边的分类讨论和
三角形三边关系D17⒈等腰三角形一个底角为80°,它的顶角为______.⒉等腰三角形一个角为80°,它的另外两个角为
__________________.⒊等腰三角形一个角为130°,它的另外两个角为___________.① 顶角+2×底角=180°② 顶角=180°-2×底角③ 底角=(180°-顶角)÷2④0°<顶角<180°
⑤0°<底角<90°结论:在等腰三角形中,注意对角的分类讨论。20 °25 °,25 °80°,20°或50°,50° 学以致用——从理论到实践巩固练习二概念:有两条边相等的三角形是等腰三角形等腰三角形是轴对称图形,顶角平分线(或底边中线或底边上的高线)所在直线是它的对称轴.1. 等腰三角形2. 能根据等腰三角形的概念与性质求等腰三角形的周长及其知道一角求其它两角或证线段、角相等
小结性质:
1 等腰三角形的两个底角相等(简写成“等边对等角”);
2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。(可简记为“三线合一”)
作业谢谢大家!谢谢合作
② ∠BAD=∠CDA
③∠ADC= ∠ADB=900
边: ④BD = CD → 两个底角相等
→ AD为顶角∠BAC的平分线
→ AD为底边BC上的高
→ AD为底边BC上的中线
结论: 等腰三角形是轴对称图形;
等腰三角形性质
性质1 等腰三角形的两个底角相等(简写成“等边对等角”);
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。(可简记为“三线合一”)对称轴是顶角平分线(底边上的中线、底边上的高线)所在直线。 等腰三角形性质
性质1 等腰三角形的两个底角相等(简
写成“等边对等角”);
性质2 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合。
(可简记为“三线合一”)数学语言性质1: 在△ABC中, ∵ AB=AC ∴ ∠ABC=?ACB
性质2: ( 1 ) ∵ AB=AC AD是角平分线,
∴ ⊥ , ____=_____ ;
( 2 ) ∵ AB=AC AD是中线,
∴ ⊥ ,∴∠ = ∠____;
( 3 ) ∵ AB=AC AD⊥BC,
∴∠_____=∠______,_____=______ 。
BAD CADBAD CAD
AD BCAD BCBD CDBD CD已知: ΔABC中,AB=AC等腰三角形的性质JG继续DZ 求证:(1)∠B=∠C
在△ABC中,若AB=AC,则∠ABC=?ACB.等腰三角形的性质证明:①作底边BC的中线AD.
思维展示AABCDD证明:作顶角的平分线AD即∠BAD=∠CAD
在△ABD和△ACD中
AB=AC
∠BAD=∠CAD
AD=AD
∴ △ABD≌ △ACD (SAS)
∴ ∠B= ∠C (全等三角形对应角相等)
作AD垂直BC于D。D已知:如图,在ΔABC中,AB=AC
求证:∠B=∠C
证明:即∠BAD=∠CAD=900
在Rt △BAD与 Rt △CAD 中∵AB=AC AD=AD
∴ Rt △BAD≌ Rt △CAD (HL)
D作△ABC的中线AD,交底边BC于D。 D┌作△ABC的高AD,垂直底边BC于D。D12作顶角的平分线AD.AABDCBDC等腰三角形常见辅助线归纳总结归纳总结 等腰三角形性质
性质2 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合。
(可简记为“三线合一”)性质2:在△ABC中, ( 1 ) ∵ AB=AC AD是角平分线,
∴ ⊥ , ____=_____ ;
( 2 ) ∵ AB=AC AD是中线,
∴ ⊥ ,∴∠ = ∠____;
( 3 ) ∵ AB=AC AD⊥BC,
∴∠_____=∠______,_____=______ 。
BAD CADBAD CAD
AD BCAD BCBD CDBD CD数学语言 学以致用——从理论到实践巩固练习一1、已知等腰三角形的两边长分别是4和6,则它的周长是( )
A、14 B、15 C、16 D、14或16
2、若把此等腰三角形的两边长改为3和7,则它的周长应是多少?
结论:在等腰三角形中,注意对边的分类讨论和
三角形三边关系D17⒈等腰三角形一个底角为80°,它的顶角为______.⒉等腰三角形一个角为80°,它的另外两个角为
__________________.⒊等腰三角形一个角为130°,它的另外两个角为___________.① 顶角+2×底角=180°② 顶角=180°-2×底角③ 底角=(180°-顶角)÷2④0°<顶角<180°
⑤0°<底角<90°结论:在等腰三角形中,注意对角的分类讨论。20 °25 °,25 °80°,20°或50°,50° 学以致用——从理论到实践巩固练习二概念:有两条边相等的三角形是等腰三角形等腰三角形是轴对称图形,顶角平分线(或底边中线或底边上的高线)所在直线是它的对称轴.1. 等腰三角形2. 能根据等腰三角形的概念与性质求等腰三角形的周长及其知道一角求其它两角或证线段、角相等
小结性质:
1 等腰三角形的两个底角相等(简写成“等边对等角”);
2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。(可简记为“三线合一”)
作业谢谢大家!谢谢合作
