沪科版九年级数学上册22.1-22.3测验题
文档属性
| 名称 | 沪科版九年级数学上册22.1-22.3测验题 |

|
|
| 格式 | rar | ||
| 文件大小 | 138.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-26 00:00:00 | ||
图片预览


文档简介
新博初中九年级数学测验题(二)
一、选择题(本大题共10小题,每小题4分,共40分)
1.二次函数的最小值是…………………………………………【 】
A. B. C. D.
2.二次函数y=-(x+1)2+3的图象的顶点坐标是…………………………【 】
A.(-1,3) B.(1,3) C.(-1,-3) D.(1,-3
3.抛物线y=2x2+4x-3的顶点坐标是 ……………………………………【 】
A.(1,-5) B.(-1,-5) C.(-1,-4) D.(-2,-7)
4.抛物线的对称轴是 …………………………………………【 】
A.直线 B.直线 C.直线 D.直线
5.二次函数图象的开口方向、对称轴和顶点坐标分别为…【 】
A.开口向下,对称轴为,顶点坐标为(3,5)
B.开口向下,对称轴为,顶点坐标为(3,5)
C.开口向上,对称轴为,顶点坐标为(-3,5)
D.开口向上,对称轴为,顶点坐标为(-3,5)
6.与抛物线y=x2-2x-4关于x轴对称的图象表示为………………………【 】
A.y=-x2+2x+4. B.y=-x2+2x-4.
C.y=x2-2x+6. D.y=x2-2x-4.
7.把抛物线y=x2+bx+c的图象向右平移2个单位,再向下平移2个单位,所得图象的解析式是y=x2-4x+5,则有……………………………………【 】
A.b=-8,c=19 B.b=0,c=-1.
C.b=0,c=3 D.b=-8,c=15.
8.已知(2,5)、(4,5)是抛物线y=ax2+bx+c上的两点,则这个抛物线的
对称轴方程是………………………………………………………………【 】
A.x= B.x=2. C.x=4. D.x=3.
9. 人民广场中心标志性建筑处有高低不同的各种喷泉,其中一支高度为1
米的喷水管喷水最大高度为3米,此时喷水水平距离为米,在如图所示
的坐标系中,这支喷泉的函数关系式是…………………………………【 】
A. B.
C. D.
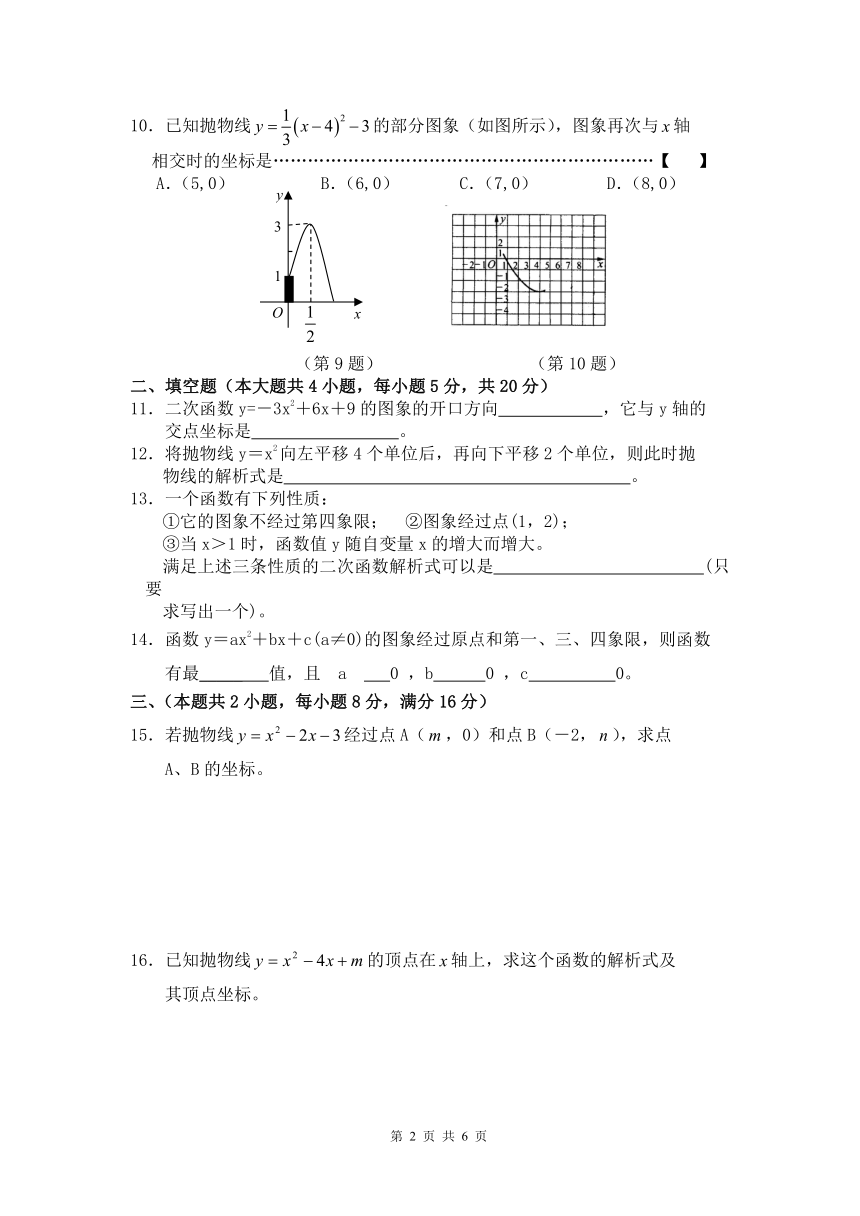
10.已知抛物线的部分图象(如图所示),图象再次与轴
相交时的坐标是…………………………………………………………【 】
A.(5,0) B.(6,0) C.(7,0) D.(8,0)
(第9题) (第10题)
二、填空题(本大题共4小题,每小题5分,共20分)
11.二次函数y=-3x2+6x+9的图象的开口方向 ,它与y轴的
交点坐标是 。
12.将抛物线y=x2向左平移4个单位后,再向下平移2个单位,则此时抛
物线的解析式是 。
13.一个函数有下列性质:
①它的图象不经过第四象限; ②图象经过点(1,2);
③当x>1时,函数值y随自变量x的增大而增大。
满足上述三条性质的二次函数解析式可以是 (只要
求写出一个)。
14.函数y=ax2+bx+c(a≠0)的图象经过原点和第一、三、四象限,则函数
有最_____ 值,且 a 0 ,b 0 ,c 0。
三、(本题共2小题,每小题8分,满分16分)
15.若抛物线经过点A(,0)和点B(-2,),求点
A、B的坐标。
16.已知抛物线的顶点在轴上,求这个函数的解析式及
其顶点坐标。
四、(本题共2小题,每小题8分,满分16分)
17. 如图,P为抛物线y=上对称轴右侧的一点,且点P在x
轴上方,过点P作PA垂直x轴于点A,PB垂直y轴于点B,得到矩
形PAOB.若AP=1,求矩形PAOB的面积。
18.已知二次函数的图象的对称轴为x=1,函数的最大值为-6,且图象经
过点(2,-8),求此二次函数的表达式。
五、(本题共2小题,每小题10分,满分20分)
19.已知二次函数的图象的顶点坐标为(3,-2)且与轴交与(0,)
(1)求函数的解析式,并画出它的图象;
(2)当为何值时,随增大而增大。
20.廊桥是我国古老的文化遗产。如图,是某座抛物线型的廊桥示意图,已
知抛物线的函数表达式为 HYPERLINK "http://www./Index.html" ,为保护廊桥的安全,在该抛
物线上距水面AB高为8米的点E、F处要安装两盏警示灯,求这两盏
灯的水平距离EF(精确到1米)。
六、(本大题满分12分)
21.如图所示,一座抛物线型拱桥,桥下水面宽度是4m,拱高是2m,当水面下降1m后,水面宽度是多少?( HYPERLINK "http://www./Index.html" ,结果保留0.1m)
七、(本大题满分12分)
22.某工厂现有80机器,每台机器平均每天生产384件产品.现准备增加一
批同类机器以提高生产总量,在试生产中发现,由于其他生产条件没变,
因此每增加一台机器,每台机器平均每天将少生产4件产品。
⑴如果增加x台机器,每天的生产总量为y件,请你写出y与x之间的
关系式;
⑵增加多少台机器,可以使每天的生产总量最大?最大生产总量是多
少?
八、(本大题满分14分)
23.在平面直角坐标系中,△AOB的位置如图5所示.已知∠AOB=90°,
AO=BO,点A的坐标为(-3,1)。
(1)求点B的坐标;
(2)求过A,O,B三点的抛物线的解析式;
(3)设点B关于抛物线的对称轴l的对称点为Bl,求△AB1 B的面积.。
答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B A B A C D C C
11. 下、(0,9) ; 12. y=(x+4)2-2(或y=x2+8x+14)
13. y=(x-1)2+2(答案不唯一); 14.大、<、>、=
15.A的坐标为(3,0),(-1,0),B的坐标为(5,0)。
16.,顶点坐标为(2,0)。
17.由y= =1得:。
矩形PAOB的面积为1+ 。
18.解:由题意设y=a(x-h)2+k,
∵x=1时,有最大值-6,
∴y=a(x-1)2-6,
又∵图象经过点(2, -8),
∴-8=a(2-1)2-6,解得a=-2,
∴该二次函数的表达式为:y=-2(x-1)2-6,即y=-2x2+4x-8。
19.(1);图略;
(2)当时,随增大而增大。
20.由于两盏E、F距离水面都是8m,因而两盏景观灯之间的水平距离就
是直线y=8与抛物线两交点的横坐标差的绝对值。
故有-x2+10 = 8,即x2=80,x1= HYPERLINK "http://www./Index.html" , x2=- HYPERLINK "http://www./Index.html" 。
所以两盏警示灯之间的水平距离为:
|x1-x2|=|-(-)|=8≈18(m)。
21.解:以水面所在的直线为x轴,以这座抛物线型拱桥的对称轴为y轴,
建立直角坐标系。
设抛物线的函数关系式为:
∵抛物线过点(0,2),∴有
又∵抛物线经过点(2,0),所以有,解得a=。
∴。
水面下降1m,即-1=,解得。
∴水面宽度为2。
22.⑴根据题意,得y=(80+x)(384-4x)=-4x2+64x+30720。
⑵∵y=-4x2+64x+30720=-4(x-8)2+30976,∴当x=8时,y最大=30976。
即增加8台机器,可以使每天的生产总量最大,最大生产总量是30976件。
23.(1)如图,作AC⊥x轴,BD⊥x轴,垂足分别为C,D,则∠ACO=
∠ODB=90°。所以∠AOC+∠OAC=90°。
又∠AOB=90°,所以∠AOC+∠BOD=90°。所以∠OAC=∠BOD。
又AO=BO,所以△ACO≌△ODB。
所以OD=AC=1,DB=OC=3。所以点B的坐标为(1,3)。
(2)抛物线过原点,可设所求抛物线的解析式为y=ax2+bx,
将A(-3,1),B(1,3)代入,得,解得
故所求抛物线的解析式为y=x2+x。
(3)抛物线y=x2+x的对称轴l的方程是x=-=-。
所以由抛物线的对称轴方程x= HYPERLINK "http://www./Index.html" ,得:-=,
解得x1=-,
所以求得点B关于抛物线的对称轴l的对称点为B1(-,3)。
在△AB1B,底边BlB=,高为2。
所以S△AB1B=××2=。
班级 姓名 学号
-------------------------------------------------密--------------------------------------------封--------------------------------------------线------------------------------------
O
x
1
3
y
_
P
_
B
_
A
_
y
_
x
_
O
O
A
E
F
B
第 1 页 共 5 页
一、选择题(本大题共10小题,每小题4分,共40分)
1.二次函数的最小值是…………………………………………【 】
A. B. C. D.
2.二次函数y=-(x+1)2+3的图象的顶点坐标是…………………………【 】
A.(-1,3) B.(1,3) C.(-1,-3) D.(1,-3
3.抛物线y=2x2+4x-3的顶点坐标是 ……………………………………【 】
A.(1,-5) B.(-1,-5) C.(-1,-4) D.(-2,-7)
4.抛物线的对称轴是 …………………………………………【 】
A.直线 B.直线 C.直线 D.直线
5.二次函数图象的开口方向、对称轴和顶点坐标分别为…【 】
A.开口向下,对称轴为,顶点坐标为(3,5)
B.开口向下,对称轴为,顶点坐标为(3,5)
C.开口向上,对称轴为,顶点坐标为(-3,5)
D.开口向上,对称轴为,顶点坐标为(-3,5)
6.与抛物线y=x2-2x-4关于x轴对称的图象表示为………………………【 】
A.y=-x2+2x+4. B.y=-x2+2x-4.
C.y=x2-2x+6. D.y=x2-2x-4.
7.把抛物线y=x2+bx+c的图象向右平移2个单位,再向下平移2个单位,所得图象的解析式是y=x2-4x+5,则有……………………………………【 】
A.b=-8,c=19 B.b=0,c=-1.
C.b=0,c=3 D.b=-8,c=15.
8.已知(2,5)、(4,5)是抛物线y=ax2+bx+c上的两点,则这个抛物线的
对称轴方程是………………………………………………………………【 】
A.x= B.x=2. C.x=4. D.x=3.
9. 人民广场中心标志性建筑处有高低不同的各种喷泉,其中一支高度为1
米的喷水管喷水最大高度为3米,此时喷水水平距离为米,在如图所示
的坐标系中,这支喷泉的函数关系式是…………………………………【 】
A. B.
C. D.
10.已知抛物线的部分图象(如图所示),图象再次与轴
相交时的坐标是…………………………………………………………【 】
A.(5,0) B.(6,0) C.(7,0) D.(8,0)
(第9题) (第10题)
二、填空题(本大题共4小题,每小题5分,共20分)
11.二次函数y=-3x2+6x+9的图象的开口方向 ,它与y轴的
交点坐标是 。
12.将抛物线y=x2向左平移4个单位后,再向下平移2个单位,则此时抛
物线的解析式是 。
13.一个函数有下列性质:
①它的图象不经过第四象限; ②图象经过点(1,2);
③当x>1时,函数值y随自变量x的增大而增大。
满足上述三条性质的二次函数解析式可以是 (只要
求写出一个)。
14.函数y=ax2+bx+c(a≠0)的图象经过原点和第一、三、四象限,则函数
有最_____ 值,且 a 0 ,b 0 ,c 0。
三、(本题共2小题,每小题8分,满分16分)
15.若抛物线经过点A(,0)和点B(-2,),求点
A、B的坐标。
16.已知抛物线的顶点在轴上,求这个函数的解析式及
其顶点坐标。
四、(本题共2小题,每小题8分,满分16分)
17. 如图,P为抛物线y=上对称轴右侧的一点,且点P在x
轴上方,过点P作PA垂直x轴于点A,PB垂直y轴于点B,得到矩
形PAOB.若AP=1,求矩形PAOB的面积。
18.已知二次函数的图象的对称轴为x=1,函数的最大值为-6,且图象经
过点(2,-8),求此二次函数的表达式。
五、(本题共2小题,每小题10分,满分20分)
19.已知二次函数的图象的顶点坐标为(3,-2)且与轴交与(0,)
(1)求函数的解析式,并画出它的图象;
(2)当为何值时,随增大而增大。
20.廊桥是我国古老的文化遗产。如图,是某座抛物线型的廊桥示意图,已
知抛物线的函数表达式为 HYPERLINK "http://www./Index.html" ,为保护廊桥的安全,在该抛
物线上距水面AB高为8米的点E、F处要安装两盏警示灯,求这两盏
灯的水平距离EF(精确到1米)。
六、(本大题满分12分)
21.如图所示,一座抛物线型拱桥,桥下水面宽度是4m,拱高是2m,当水面下降1m后,水面宽度是多少?( HYPERLINK "http://www./Index.html" ,结果保留0.1m)
七、(本大题满分12分)
22.某工厂现有80机器,每台机器平均每天生产384件产品.现准备增加一
批同类机器以提高生产总量,在试生产中发现,由于其他生产条件没变,
因此每增加一台机器,每台机器平均每天将少生产4件产品。
⑴如果增加x台机器,每天的生产总量为y件,请你写出y与x之间的
关系式;
⑵增加多少台机器,可以使每天的生产总量最大?最大生产总量是多
少?
八、(本大题满分14分)
23.在平面直角坐标系中,△AOB的位置如图5所示.已知∠AOB=90°,
AO=BO,点A的坐标为(-3,1)。
(1)求点B的坐标;
(2)求过A,O,B三点的抛物线的解析式;
(3)设点B关于抛物线的对称轴l的对称点为Bl,求△AB1 B的面积.。
答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B A B A C D C C
11. 下、(0,9) ; 12. y=(x+4)2-2(或y=x2+8x+14)
13. y=(x-1)2+2(答案不唯一); 14.大、<、>、=
15.A的坐标为(3,0),(-1,0),B的坐标为(5,0)。
16.,顶点坐标为(2,0)。
17.由y= =1得:。
矩形PAOB的面积为1+ 。
18.解:由题意设y=a(x-h)2+k,
∵x=1时,有最大值-6,
∴y=a(x-1)2-6,
又∵图象经过点(2, -8),
∴-8=a(2-1)2-6,解得a=-2,
∴该二次函数的表达式为:y=-2(x-1)2-6,即y=-2x2+4x-8。
19.(1);图略;
(2)当时,随增大而增大。
20.由于两盏E、F距离水面都是8m,因而两盏景观灯之间的水平距离就
是直线y=8与抛物线两交点的横坐标差的绝对值。
故有-x2+10 = 8,即x2=80,x1= HYPERLINK "http://www./Index.html" , x2=- HYPERLINK "http://www./Index.html" 。
所以两盏警示灯之间的水平距离为:
|x1-x2|=|-(-)|=8≈18(m)。
21.解:以水面所在的直线为x轴,以这座抛物线型拱桥的对称轴为y轴,
建立直角坐标系。
设抛物线的函数关系式为:
∵抛物线过点(0,2),∴有
又∵抛物线经过点(2,0),所以有,解得a=。
∴。
水面下降1m,即-1=,解得。
∴水面宽度为2。
22.⑴根据题意,得y=(80+x)(384-4x)=-4x2+64x+30720。
⑵∵y=-4x2+64x+30720=-4(x-8)2+30976,∴当x=8时,y最大=30976。
即增加8台机器,可以使每天的生产总量最大,最大生产总量是30976件。
23.(1)如图,作AC⊥x轴,BD⊥x轴,垂足分别为C,D,则∠ACO=
∠ODB=90°。所以∠AOC+∠OAC=90°。
又∠AOB=90°,所以∠AOC+∠BOD=90°。所以∠OAC=∠BOD。
又AO=BO,所以△ACO≌△ODB。
所以OD=AC=1,DB=OC=3。所以点B的坐标为(1,3)。
(2)抛物线过原点,可设所求抛物线的解析式为y=ax2+bx,
将A(-3,1),B(1,3)代入,得,解得
故所求抛物线的解析式为y=x2+x。
(3)抛物线y=x2+x的对称轴l的方程是x=-=-。
所以由抛物线的对称轴方程x= HYPERLINK "http://www./Index.html" ,得:-=,
解得x1=-,
所以求得点B关于抛物线的对称轴l的对称点为B1(-,3)。
在△AB1B,底边BlB=,高为2。
所以S△AB1B=××2=。
班级 姓名 学号
-------------------------------------------------密--------------------------------------------封--------------------------------------------线------------------------------------
O
x
1
3
y
_
P
_
B
_
A
_
y
_
x
_
O
O
A
E
F
B
第 1 页 共 5 页
