初中数学》冀教版》冀教版九年级下册》第三十五章 圆(二)》35.1 点与圆的位置关系
文档属性
| 名称 | 初中数学》冀教版》冀教版九年级下册》第三十五章 圆(二)》35.1 点与圆的位置关系 |

|
|
| 格式 | rar | ||
| 文件大小 | 581.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-27 10:38:00 | ||
图片预览

文档简介
点与圆的位置关系 教学设计
教学设计思想:本课从问题情景:要学生解难入手,建立模型,设下悬念,然后让学生探究二个问题,将探究的结论应用解决实际问题。本课的一个关键点就是围绕着学生活动来展开,由学生身边的事所引出的数学问题使学生体会到数学与生活的紧密和谐的关系。朴素的问题情景(射击、踢球)自然对学生产生了一种情感上的亲和力和感召力,增强了学生自主参与性;通过观察、操作、思考、解释、合作等教学活动过程,使学生体会到了创造的乐趣和成功的喜悦,还能感受到数学与自我生存的关系。
教学目标:
1.知识与技能
探索并掌握点与圆的三种位置关系及这三种位置关系对应的圆的半径r与点到圆心的距离d之间的数量关系。
2.过程与方法
经历探索点与圆的三种位置关系的过程,体会数学分类讨论思考问题的方法。
3.情感、态度与价值观
通过本节课的学习,渗透数形结合的思想和运动变化的观点的教育。
教学重点:用数量关系判断点与圆的位置关系。
教学难点:判断点与圆的位置关系。
教学方法:发现法;引导法。
教学媒体:幻灯片、画板,直尺。
教学安排:1课时。
教学过程:
Ⅰ.创设问题情境,引入新知
同学们看过奥运会的射击比赛吗?射击的靶子是由许多圆组成的,射击的成绩是由击中靶子不同位置所决定的;下图是一位运动员射击10发子弹在靶上留下的痕迹。
思考:在这个图中有哪些图形?(圆、点)
这个图形体现了平面上的点与圆的位置关系,我们今天这节课就来研究这个问题,课题:点与圆的位置关系。
Ⅱ.合作探索交流,探索新知
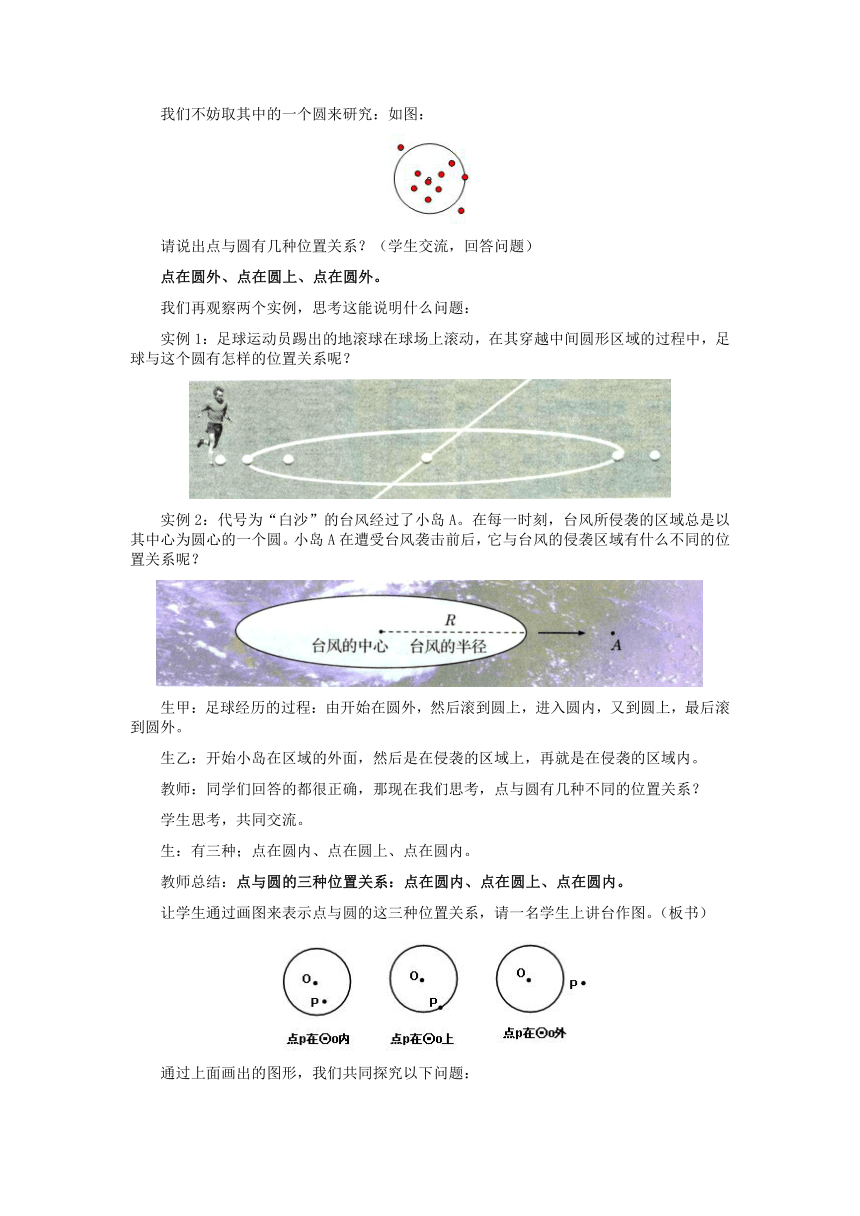
我们不妨取其中的一个圆来研究:如图:
请说出点与圆有几种位置关系?(学生交流,回答问题)
点在圆外、点在圆上、点在圆外。
我们再观察两个实例,思考这能说明什么问题:
实例1:足球运动员踢出的地滚球在球场上滚动,在其穿越中间圆形区域的过程中,足球与这个圆有怎样的位置关系呢?
实例2:代号为“白沙”的台风经过了小岛A。在每一时刻,台风所侵袭的区域总是以其中心为圆心的一个圆。小岛A在遭受台风袭击前后,它与台风的侵袭区域有什么不同的位置关系呢?
生甲:足球经历的过程:由开始在圆外,然后滚到圆上,进入圆内,又到圆上,最后滚到圆外。
生乙:开始小岛在区域的外面,然后是在侵袭的区域上,再就是在侵袭的区域内。
教师:同学们回答的都很正确,那现在我们思考,点与圆有几种不同的位置关系?
学生思考,共同交流。
生:有三种;点在圆内、点在圆上、点在圆内。
教师总结:点与圆的三种位置关系:点在圆内、点在圆上、点在圆内。
让学生通过画图来表示点与圆的这三种位置关系,请一名学生上讲台作图。(板书)
通过上面画出的图形,我们共同探究以下问题:
1.在你画出的三幅图中,分别测量点到圆心的距离d,并与圆的半径r的大小比较大小。
学生动手,测量并记录结果。
2.点与圆的三种位置关系所对应的r与d的数量关系分别是怎样的?与同学交流并填写下表:
语言描述 图形表示 r与d的数量关系
点在圆内
点在圆上
点在圆外
通过第一步的测量,我们得出结果:
点在圆内:r>d;
点在圆上:r=d;
点在圆外:r3.如果圆的半径r与点到圆心的距离d的关系分别是rd,请分别指出点与圆的位置关系。
教师总结:我们知道圆上的所有点到圆心的距离都等于半径,若点在圆上,那么这个点到圆心的距离等于半径;若点到圆外,那么这个点到圆心的距离大于半径;若点在圆内,那么这个点到圆心的距离小于半径。
即:(1)点在圆内d(2)点在圆上d=r。
(3)点在圆外d>r。
Ⅲ.典型例题
下面我们看一道例题:
如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以A为圆心,以3cm为半径画圆,请判断:
(1)点C与⊙A的位置关系。
(2)点B与⊙A的位置关系。
(3)AB的中点D与⊙A的位置关系。
解析:这道题是考查点与圆的位置关系,根据我们所学判断点与圆的位置关系的条件来解答。
解:由勾股定理得
代入数据得:AC==3。
当以点A为圆心,3cm为半径作圆,有r=d,故点C在⊙A上。
而AB=d=5cm,d>r=3,故点B在⊙A外。
∵点D是AB的中点,AB=5cm,
∴AD=2.5cm,d=2.5∴AB的中点D在⊙A内。
Ⅳ.课上练习
如图,某海域点A处周围3km的圆形区域为多暗礁的危险区,但水生物资源丰富,渔船要从B处前进到A处进行捕鱼作业,B、A之间的距离是10km。如果渔船始终保持10km/h的航速,那么,在什么时段内,渔船是安全的?渔船何时进入危险区域?
Ⅴ.课堂小结
板书设计:
点与圆的位置关系一、创设情景 三、例题二、新课讲授 四、练习
教学设计思想:本课从问题情景:要学生解难入手,建立模型,设下悬念,然后让学生探究二个问题,将探究的结论应用解决实际问题。本课的一个关键点就是围绕着学生活动来展开,由学生身边的事所引出的数学问题使学生体会到数学与生活的紧密和谐的关系。朴素的问题情景(射击、踢球)自然对学生产生了一种情感上的亲和力和感召力,增强了学生自主参与性;通过观察、操作、思考、解释、合作等教学活动过程,使学生体会到了创造的乐趣和成功的喜悦,还能感受到数学与自我生存的关系。
教学目标:
1.知识与技能
探索并掌握点与圆的三种位置关系及这三种位置关系对应的圆的半径r与点到圆心的距离d之间的数量关系。
2.过程与方法
经历探索点与圆的三种位置关系的过程,体会数学分类讨论思考问题的方法。
3.情感、态度与价值观
通过本节课的学习,渗透数形结合的思想和运动变化的观点的教育。
教学重点:用数量关系判断点与圆的位置关系。
教学难点:判断点与圆的位置关系。
教学方法:发现法;引导法。
教学媒体:幻灯片、画板,直尺。
教学安排:1课时。
教学过程:
Ⅰ.创设问题情境,引入新知
同学们看过奥运会的射击比赛吗?射击的靶子是由许多圆组成的,射击的成绩是由击中靶子不同位置所决定的;下图是一位运动员射击10发子弹在靶上留下的痕迹。
思考:在这个图中有哪些图形?(圆、点)
这个图形体现了平面上的点与圆的位置关系,我们今天这节课就来研究这个问题,课题:点与圆的位置关系。
Ⅱ.合作探索交流,探索新知
我们不妨取其中的一个圆来研究:如图:
请说出点与圆有几种位置关系?(学生交流,回答问题)
点在圆外、点在圆上、点在圆外。
我们再观察两个实例,思考这能说明什么问题:
实例1:足球运动员踢出的地滚球在球场上滚动,在其穿越中间圆形区域的过程中,足球与这个圆有怎样的位置关系呢?
实例2:代号为“白沙”的台风经过了小岛A。在每一时刻,台风所侵袭的区域总是以其中心为圆心的一个圆。小岛A在遭受台风袭击前后,它与台风的侵袭区域有什么不同的位置关系呢?
生甲:足球经历的过程:由开始在圆外,然后滚到圆上,进入圆内,又到圆上,最后滚到圆外。
生乙:开始小岛在区域的外面,然后是在侵袭的区域上,再就是在侵袭的区域内。
教师:同学们回答的都很正确,那现在我们思考,点与圆有几种不同的位置关系?
学生思考,共同交流。
生:有三种;点在圆内、点在圆上、点在圆内。
教师总结:点与圆的三种位置关系:点在圆内、点在圆上、点在圆内。
让学生通过画图来表示点与圆的这三种位置关系,请一名学生上讲台作图。(板书)
通过上面画出的图形,我们共同探究以下问题:
1.在你画出的三幅图中,分别测量点到圆心的距离d,并与圆的半径r的大小比较大小。
学生动手,测量并记录结果。
2.点与圆的三种位置关系所对应的r与d的数量关系分别是怎样的?与同学交流并填写下表:
语言描述 图形表示 r与d的数量关系
点在圆内
点在圆上
点在圆外
通过第一步的测量,我们得出结果:
点在圆内:r>d;
点在圆上:r=d;
点在圆外:r
教师总结:我们知道圆上的所有点到圆心的距离都等于半径,若点在圆上,那么这个点到圆心的距离等于半径;若点到圆外,那么这个点到圆心的距离大于半径;若点在圆内,那么这个点到圆心的距离小于半径。
即:(1)点在圆内d
(3)点在圆外d>r。
Ⅲ.典型例题
下面我们看一道例题:
如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以A为圆心,以3cm为半径画圆,请判断:
(1)点C与⊙A的位置关系。
(2)点B与⊙A的位置关系。
(3)AB的中点D与⊙A的位置关系。
解析:这道题是考查点与圆的位置关系,根据我们所学判断点与圆的位置关系的条件来解答。
解:由勾股定理得
代入数据得:AC==3。
当以点A为圆心,3cm为半径作圆,有r=d,故点C在⊙A上。
而AB=d=5cm,d>r=3,故点B在⊙A外。
∵点D是AB的中点,AB=5cm,
∴AD=2.5cm,d=2.5
Ⅳ.课上练习
如图,某海域点A处周围3km的圆形区域为多暗礁的危险区,但水生物资源丰富,渔船要从B处前进到A处进行捕鱼作业,B、A之间的距离是10km。如果渔船始终保持10km/h的航速,那么,在什么时段内,渔船是安全的?渔船何时进入危险区域?
Ⅴ.课堂小结
板书设计:
点与圆的位置关系一、创设情景 三、例题二、新课讲授 四、练习
