方程的根与函数的零点说课
图片预览








文档简介
课件25张PPT。
一、教材分析
1、本节内容在教材中的地位和作用
“函数与方程”这个单元体现了函数与方程、不等式、算法等内容的横向联系。
本节“方程的根与函数的零点”正体现函数与方程及数形结合重要思想,同时为下节“用二分法求方程的近似解”和后续的算法等学习内容打下基础,起着承上启下的作用。
2、教学重点:体会函数零点与方程根之间的联系,掌握零点的概念及零点存在性定理
教学难点:探究并发现零点存在性定理及其应用
二、三维目标分析
1、知识与技能
结合二次函数的图象,判断一元二次方程根的存在性及个数,从而了解函数的零点与方程的根的联系.理解并会用零点存在性定理
2、过程与方法
培养学生观察 、思考、分析、猜想、验证的能力,并从中体验从特殊到一般及函数与方程互相转化的重要思想。
3、情感态度与价值观
引导学生通过自主探究,发现问题,解决问题的过程,激发学习热情和求知欲,体现学生的主体地位,提高学习数学的兴趣 。确定三维目标的依据:初中学习过二次函数定义图象及性质和一元二次方程求法,初步认识到一元二次方程与相应二次函数的联系。
在高中阶段,学生已经学习了函数概念与性质,掌握了研究部分基本初等函数性质的思想方法. 2、学生的认知水平三、教法学法
教法:探究式教学法
教学手段:采用多媒体辅助教学,构建学生自主掌握的平台
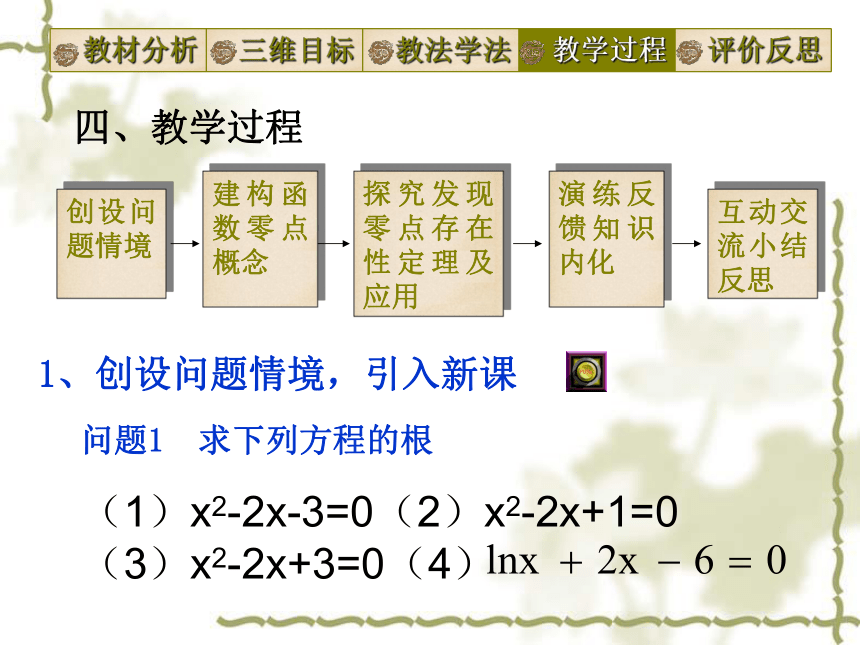
学法:观察发现 自主探索 合作交流四、教学过程
问题1 求下列方程的根
(1)x2-2x-3=0(2)x2-2x+1=0
(3)x2-2x+3=0(4)1、创设问题情境,引入新课问题2:填写下表,探究一元二次方程的根与相应二次函数与x轴的交点的关系?问题3:一元二次方程 的根与相应二次函数 图像与 x轴交点有何关系? 2、建构函数零点概念
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点。
(1)、零点是一个点吗?
(2)、怎样理解“零点”概念双向性呢?
(3)、请你说出表格中3个函数的零点及个数?
(投影问题2的表格) 方程x2-2x+1=0x2-2x+3=0y= x2-2x-3y= x2-2x+1函数函
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根函数的图象
与x轴的交点(-1,0)、(3,0)(1,0)x2-2x-3=0y= x2-2x+3请你说出表格中3个函数的零点及个数?无交点(1)方程f(x)=0有实数根知识的延伸,得出等价关系零点的求法 代数法图象法思考:问题1(4)求方程lnx+2x-6=0的根?
思考:如何求函数f(x)=lnx+2x-6的零点呢?图象0244-1-2-3-4y让学生自己任意画几个函数图象验证自己的猜想3、探究发现零点存在性定理(1)探究y思考:你能说出应用零点存在性定理应注意哪几个条件?零点存在性定理(2)发现:解:用计算器或计算机作出x、f(x)的对应值表(表3-1)
和图象(图3.1—3)例 1 求函数f(x)=lnx+2x-6的零点个数。你能给出这个函数是增函数的证明吗?4、演练反馈:双基训练,知识内化 体现方程转化为函数重要思想( )( )5、本课小结:请你谈谈本节课的收获?
1.函数零点的定义
2.等价关系
3.如何应用零点存在性定理判断函数的零点存在性以及个数培养自主探究合作的学习方式选做题:1、求证:函数在 上存在唯一零点。
必做题:
1、求函数:y=-x2+6x+7的零点
2、方程
的解所在的区间是( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
3、若函数f(x)=x2-ax-b的两个零点是2和3,求loga25 + b2。
布置作业,学以致用将学生思维引领向更高的层次探究题: 1、设函数
(1)利用计算机探求 和
时函数的零点个数;
(2)当 时,函数
的零点是怎样分布的?值得肯定的:
积极探索 勇于猜想
合作交流 敢于表达值得注意:注重用函数的思想解决方程 问题
零点存在性定理的灵活使用
五、评价与反思反馈式评价采用“启发—探究—讨论”教学模式精心设置一个个问题链,给每个学生提供思考、创造、表现和成功的机会,并进行反馈式评价。教学反思教学设计过程中注意了:
(1)在学生已有知识结构和新概念间寻找“最近发展区”
(2)设法走出“概念一带而过,演习铺天盖地”的误区,促使自己与学生一起走进“重视探究、重视交流、重视过程” 的新天地。 建构主义认为:知识不是被动接受,而是认知主体积极主动建构的。本节的教学设计正是在这种教学理念的指导下,让学生经历“创设问题情境——建构概念——探究定理——注重反思——拓展应用”的活动过程,体验参与数学知识的发生、发展过程,提高学习数学的兴趣,成为积极主动的建构者。本节课让学生充分体验并理解函数与方程相互转化的数学思想方法,是学习数形结合、函数与方程等数学思想方法很好的载体.教学设计说明§3.1.1 方程的根与函数的零点 一、函数的零点 二、三个等价关系 三、零点存在性定理 例1 求函数 的零点个数. …… 演练: (1) …… (2) …… 多 媒 体 演 示 求函数零点的方法:代数法,图象法板书设计谢谢大家莆田华侨中学 何高萍大姚在一栋楼的离地面垂直距离10米高A处斜抛一个篮球(篮球运动轨迹是一条抛物线段),已知蓝球上升到最高点M时,球离地面垂直距离为 米,离这栋楼的水平距离为1米,你能求出球落地点B离这座楼的水平距离是多少米吗?B(0,10)(1, )
一、教材分析
1、本节内容在教材中的地位和作用
“函数与方程”这个单元体现了函数与方程、不等式、算法等内容的横向联系。
本节“方程的根与函数的零点”正体现函数与方程及数形结合重要思想,同时为下节“用二分法求方程的近似解”和后续的算法等学习内容打下基础,起着承上启下的作用。
2、教学重点:体会函数零点与方程根之间的联系,掌握零点的概念及零点存在性定理
教学难点:探究并发现零点存在性定理及其应用
二、三维目标分析
1、知识与技能
结合二次函数的图象,判断一元二次方程根的存在性及个数,从而了解函数的零点与方程的根的联系.理解并会用零点存在性定理
2、过程与方法
培养学生观察 、思考、分析、猜想、验证的能力,并从中体验从特殊到一般及函数与方程互相转化的重要思想。
3、情感态度与价值观
引导学生通过自主探究,发现问题,解决问题的过程,激发学习热情和求知欲,体现学生的主体地位,提高学习数学的兴趣 。确定三维目标的依据:初中学习过二次函数定义图象及性质和一元二次方程求法,初步认识到一元二次方程与相应二次函数的联系。
在高中阶段,学生已经学习了函数概念与性质,掌握了研究部分基本初等函数性质的思想方法. 2、学生的认知水平三、教法学法
教法:探究式教学法
教学手段:采用多媒体辅助教学,构建学生自主掌握的平台
学法:观察发现 自主探索 合作交流四、教学过程
问题1 求下列方程的根
(1)x2-2x-3=0(2)x2-2x+1=0
(3)x2-2x+3=0(4)1、创设问题情境,引入新课问题2:填写下表,探究一元二次方程的根与相应二次函数与x轴的交点的关系?问题3:一元二次方程 的根与相应二次函数 图像与 x轴交点有何关系? 2、建构函数零点概念
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点。
(1)、零点是一个点吗?
(2)、怎样理解“零点”概念双向性呢?
(3)、请你说出表格中3个函数的零点及个数?
(投影问题2的表格) 方程x2-2x+1=0x2-2x+3=0y= x2-2x-3y= x2-2x+1函数函
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根函数的图象
与x轴的交点(-1,0)、(3,0)(1,0)x2-2x-3=0y= x2-2x+3请你说出表格中3个函数的零点及个数?无交点(1)方程f(x)=0有实数根知识的延伸,得出等价关系零点的求法 代数法图象法思考:问题1(4)求方程lnx+2x-6=0的根?
思考:如何求函数f(x)=lnx+2x-6的零点呢?图象0244-1-2-3-4y让学生自己任意画几个函数图象验证自己的猜想3、探究发现零点存在性定理(1)探究y思考:你能说出应用零点存在性定理应注意哪几个条件?零点存在性定理(2)发现:解:用计算器或计算机作出x、f(x)的对应值表(表3-1)
和图象(图3.1—3)例 1 求函数f(x)=lnx+2x-6的零点个数。你能给出这个函数是增函数的证明吗?4、演练反馈:双基训练,知识内化 体现方程转化为函数重要思想( )( )5、本课小结:请你谈谈本节课的收获?
1.函数零点的定义
2.等价关系
3.如何应用零点存在性定理判断函数的零点存在性以及个数培养自主探究合作的学习方式选做题:1、求证:函数在 上存在唯一零点。
必做题:
1、求函数:y=-x2+6x+7的零点
2、方程
的解所在的区间是( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
3、若函数f(x)=x2-ax-b的两个零点是2和3,求loga25 + b2。
布置作业,学以致用将学生思维引领向更高的层次探究题: 1、设函数
(1)利用计算机探求 和
时函数的零点个数;
(2)当 时,函数
的零点是怎样分布的?值得肯定的:
积极探索 勇于猜想
合作交流 敢于表达值得注意:注重用函数的思想解决方程 问题
零点存在性定理的灵活使用
五、评价与反思反馈式评价采用“启发—探究—讨论”教学模式精心设置一个个问题链,给每个学生提供思考、创造、表现和成功的机会,并进行反馈式评价。教学反思教学设计过程中注意了:
(1)在学生已有知识结构和新概念间寻找“最近发展区”
(2)设法走出“概念一带而过,演习铺天盖地”的误区,促使自己与学生一起走进“重视探究、重视交流、重视过程” 的新天地。 建构主义认为:知识不是被动接受,而是认知主体积极主动建构的。本节的教学设计正是在这种教学理念的指导下,让学生经历“创设问题情境——建构概念——探究定理——注重反思——拓展应用”的活动过程,体验参与数学知识的发生、发展过程,提高学习数学的兴趣,成为积极主动的建构者。本节课让学生充分体验并理解函数与方程相互转化的数学思想方法,是学习数形结合、函数与方程等数学思想方法很好的载体.教学设计说明§3.1.1 方程的根与函数的零点 一、函数的零点 二、三个等价关系 三、零点存在性定理 例1 求函数 的零点个数. …… 演练: (1) …… (2) …… 多 媒 体 演 示 求函数零点的方法:代数法,图象法板书设计谢谢大家莆田华侨中学 何高萍大姚在一栋楼的离地面垂直距离10米高A处斜抛一个篮球(篮球运动轨迹是一条抛物线段),已知蓝球上升到最高点M时,球离地面垂直距离为 米,离这栋楼的水平距离为1米,你能求出球落地点B离这座楼的水平距离是多少米吗?B(0,10)(1, )
