(新人教b必修5)数学:1.2《正、余弦定理的应用》课件
文档属性
| 名称 | (新人教b必修5)数学:1.2《正、余弦定理的应用》课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 689.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-27 00:00:00 | ||
图片预览






文档简介
课件16张PPT。正余弦定理的应用1、角的关系
2、边的关系
3、边角关系大角对大边 大边对大角
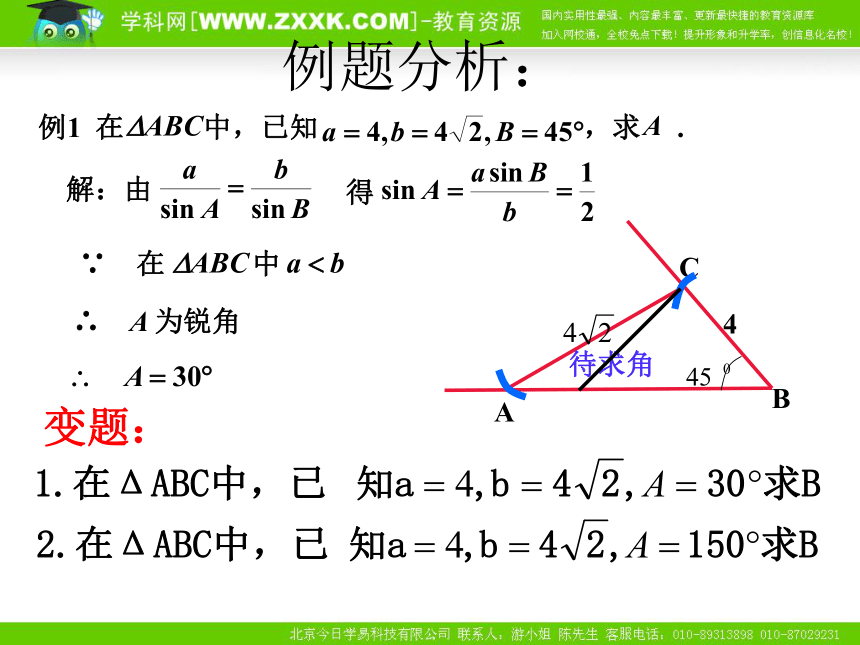
三角形中的边角关系∴ A 为锐角 例题分析:变题:ABC4待求角例题分析:(04北京)在△ABC中,a,b,c分别是A,B,C的对边长,已知a,b,c成等比数列,且
(1)求A的大小
(2)
(04北京)在△ABC中,a,b,c分别是A,B,C的对边长,已知a,b,c成等比数列,且
(1)求A的大小 (2)解(1)在△ABC中,由余弦定理得在△ABC中,由正弦定理得解(2)(04北京)在△ABC中,a,b,c分别是A,B,C的对边长,已知a,b,c成等比数列,且
(1)求A的大小 (2)解(2)法一:法二:(04北京)在△ABC中,a,b,c分别是A,B,C的对边长,已知a,b,c成等比数列,且
(1)求A的大小 (2)练习:例3.在△ABC中,
(a2+b2)sin(A-B)=(a2-b2)sin(A+B)
判断△ABC的形状. 例题分析:分析:例3.在△ABC中,
(a2+b2)sin(A-B)=(a2-b2)sin(A+B)
判断△ABC的形状. 即为△ABC等腰三角形或直角三角形思路一:思路二:思路三:练习:思考题:在△ABC中设
命题p:
命题q: △ABC是等边三角形,那么
命题p是命题q的( )A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既充分也不必要条件C结论思考题:1、已知在△ABC中,角A、B、C 的对
边分别为a、b、c . 向量
且
(1)求角C.
(2)若 ,试求 的值.思考题:3.在△ABC中,三边a、b、c满足
(a+b+c)(a+b-c)= ab,求tanC.
2、边的关系
3、边角关系大角对大边 大边对大角
三角形中的边角关系∴ A 为锐角 例题分析:变题:ABC4待求角例题分析:(04北京)在△ABC中,a,b,c分别是A,B,C的对边长,已知a,b,c成等比数列,且
(1)求A的大小
(2)
(04北京)在△ABC中,a,b,c分别是A,B,C的对边长,已知a,b,c成等比数列,且
(1)求A的大小 (2)解(1)在△ABC中,由余弦定理得在△ABC中,由正弦定理得解(2)(04北京)在△ABC中,a,b,c分别是A,B,C的对边长,已知a,b,c成等比数列,且
(1)求A的大小 (2)解(2)法一:法二:(04北京)在△ABC中,a,b,c分别是A,B,C的对边长,已知a,b,c成等比数列,且
(1)求A的大小 (2)练习:例3.在△ABC中,
(a2+b2)sin(A-B)=(a2-b2)sin(A+B)
判断△ABC的形状. 例题分析:分析:例3.在△ABC中,
(a2+b2)sin(A-B)=(a2-b2)sin(A+B)
判断△ABC的形状. 即为△ABC等腰三角形或直角三角形思路一:思路二:思路三:练习:思考题:在△ABC中设
命题p:
命题q: △ABC是等边三角形,那么
命题p是命题q的( )A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既充分也不必要条件C结论思考题:1、已知在△ABC中,角A、B、C 的对
边分别为a、b、c . 向量
且
(1)求角C.
(2)若 ,试求 的值.思考题:3.在△ABC中,三边a、b、c满足
(a+b+c)(a+b-c)= ab,求tanC.
