(新人教b必修5)数学:3.3《一元二次不等式及其解法》
文档属性
| 名称 | (新人教b必修5)数学:3.3《一元二次不等式及其解法》 |

|
|
| 格式 | rar | ||
| 文件大小 | 73.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-27 00:00:00 | ||
图片预览







文档简介
课件20张PPT。3.3 一元二次不等式及其
解法考察下面含未知数x的不等式: 15x2+30x-1>0 和 3x2+6x-1≤0.这两个不等式有两个共同特点: (1)含有一个未知数x;
(2)未知数的最高次数为2. 一般地,含有一个未知数,且未知数的最高次数为2的整式不等式,叫做一元二次不等式。 一元二次不等式的一般表达式为 ax2+bx+c>0 (a≠0),或ax2+bx+c<0 (a≠0)其中a,b,c均为常数。 一元二次不等式一般表达式的左边,恰是关于自变量x的二次函数f(x)的解析式,
即 f(x)=ax2+bx+c (a≠0), 一元二次不等式f(x)>0,或f(x)<0 (a≠0)的解集,就是分别使二次函数f(x)的函数值为正值或负值时自变量x的取值的集合。 一元二次方程f(x)=0 (a≠0)的解集,就是使二次函数f(x)为零时自变量x的取值的集合。 因此二次函数,一元二次方程,一元二次不等式之间有非常密切的联系。 下面我们通过实例,研究一元二次不等式的解法,以及它与相应的方程、函数之间的关系。例如解不等式:
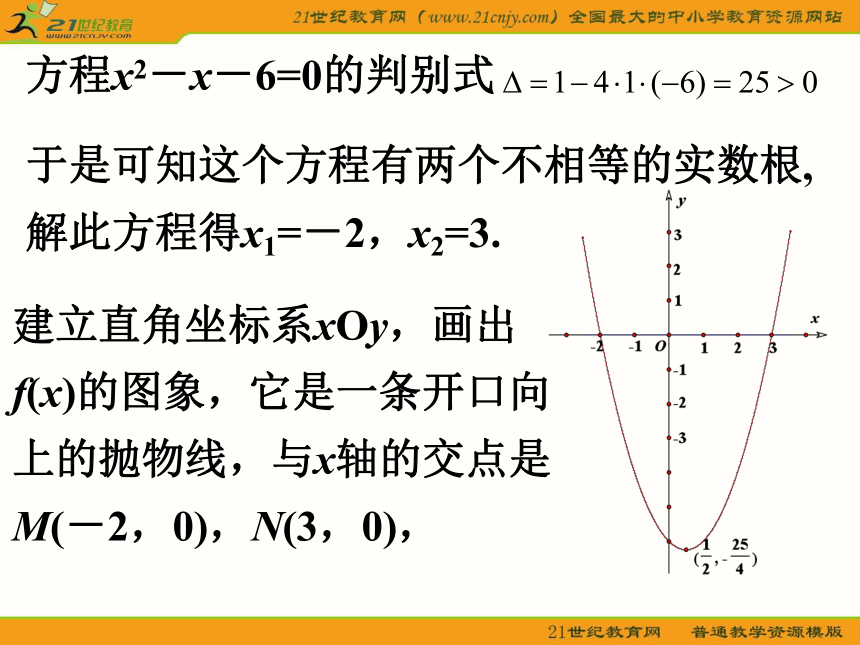
(1)x2-x-6>0;(2)x2-x-6<0. 建立直角坐标系xOy,画出f(x)的图象,它是一条开口向上的抛物线,与x轴的交点是M(-2,0),N(3,0), 观察这个图象,可以看出,抛物线位于x轴上方的点的纵坐标大于零,因此这些点的横坐标的集合
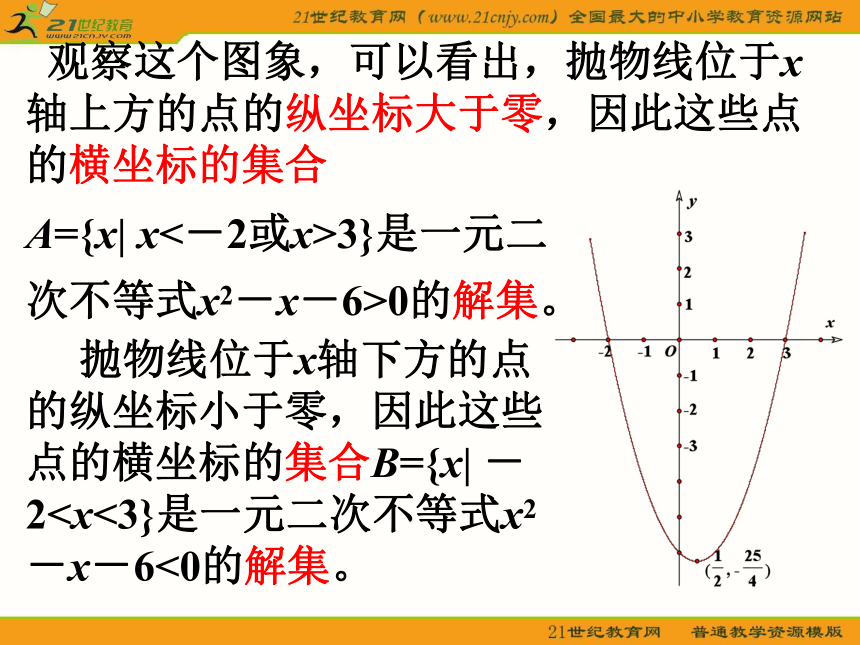
A={x| x<-2或x>3}是一元二
次不等式x2-x-6>0的解集。 抛物线位于x轴下方的点的纵坐标小于零,因此这些点的横坐标的集合B={x| -2(x+2)(x-3)>0; 若x>3,同样可推知(x+2)(x-3)>0。 当x∈B时,即-20,
x-3<0,因此(x+2)(x-3)<0, 不等式(1)和(2)还可以通过下述方法求解: 比较上面的两种解法,可以明显地体会到,作出相应的二次函数的图象,并由图象直接写出解集的方法更简便一些。例1.解不等式:(1)x2-2x+3>0;
(2)x2-2x+3<0.分析:考察方程x2-2x+3=0的判别式△=(-2)2-4×1×3<0,二次函数的图象位于x轴的上方(如图),这时对于任意的实数x,都有x2-2x+3>0。 解:对于任意实数x,
x2-2x+3=(x-1)2+2>0,
因此不等式(1)的解集为实数集R,
不等式(2)无解,或说它的解集为空集. 通过以上两例,我们不难对一元二次不等式ax2+bx+c>0 (a>0)和ax2+bx+c<0 (a>0)解集的形式作一般性的分析。 设方程ax2+bx+c=0 (a>0)的判别式为△。(1)当△>0时,二次方程ax2+bx+c=0有两个不等的实数根x1,x2,(设x10的解集是(-∞,x1)∪ (x2,+∞),不等式ax2+bx+c<0的解集是(x1,x2).简单的说是:
大于在两边,小于在中间。(2)当△=0时,通过配方得, 由图可知,ax2+bx+c>0的解集是 的全体实数,即
ax2+bx+c<0的解集是空集,即不等式无解。(3)当△<0时,二次函数f(x)=ax2+bx+c的图象在x轴上方,由此可知,不等式ax2+bx+c>0的解集是实数集R,不等式ax2+bx+c<0的解集是空集。例2.解不等式1-x-4x2>0.解:原不等式化为4x2+x-1<0,
因为△=12-4×4×(-1)>0,
方程4x2+x-1=0的根是所以不等式的解集是 例3.解不等式x2+4x+4>0.解:因为△=42-4×1×4=0,
原不等式化为(x+2)2>0,
所以不等式的解集是{x∈R| x≠-2}.例4.解不等式-2x2+4x-3>0.解:原不等式化为2x2-4x+3<0,
因为2x2-4x+3=2(x-1)2+1>0,
所以原不等式的解集是解:由函数f(x)的解析式有意义得 即 解得 因此1≤x<3,所求函数的定义域是[1,3).
(2)未知数的最高次数为2. 一般地,含有一个未知数,且未知数的最高次数为2的整式不等式,叫做一元二次不等式。 一元二次不等式的一般表达式为 ax2+bx+c>0 (a≠0),或ax2+bx+c<0 (a≠0)其中a,b,c均为常数。 一元二次不等式一般表达式的左边,恰是关于自变量x的二次函数f(x)的解析式,
即 f(x)=ax2+bx+c (a≠0), 一元二次不等式f(x)>0,或f(x)<0 (a≠0)的解集,就是分别使二次函数f(x)的函数值为正值或负值时自变量x的取值的集合。 一元二次方程f(x)=0 (a≠0)的解集,就是使二次函数f(x)为零时自变量x的取值的集合。 因此二次函数,一元二次方程,一元二次不等式之间有非常密切的联系。 下面我们通过实例,研究一元二次不等式的解法,以及它与相应的方程、函数之间的关系。例如解不等式:
(1)x2-x-6>0;(2)x2-x-6<0. 建立直角坐标系xOy,画出f(x)的图象,它是一条开口向上的抛物线,与x轴的交点是M(-2,0),N(3,0), 观察这个图象,可以看出,抛物线位于x轴上方的点的纵坐标大于零,因此这些点的横坐标的集合
A={x| x<-2或x>3}是一元二
次不等式x2-x-6>0的解集。 抛物线位于x轴下方的点的纵坐标小于零,因此这些点的横坐标的集合B={x| -2
x-3<0,因此(x+2)(x-3)<0, 不等式(1)和(2)还可以通过下述方法求解: 比较上面的两种解法,可以明显地体会到,作出相应的二次函数的图象,并由图象直接写出解集的方法更简便一些。例1.解不等式:(1)x2-2x+3>0;
(2)x2-2x+3<0.分析:考察方程x2-2x+3=0的判别式△=(-2)2-4×1×3<0,二次函数的图象位于x轴的上方(如图),这时对于任意的实数x,都有x2-2x+3>0。 解:对于任意实数x,
x2-2x+3=(x-1)2+2>0,
因此不等式(1)的解集为实数集R,
不等式(2)无解,或说它的解集为空集. 通过以上两例,我们不难对一元二次不等式ax2+bx+c>0 (a>0)和ax2+bx+c<0 (a>0)解集的形式作一般性的分析。 设方程ax2+bx+c=0 (a>0)的判别式为△。(1)当△>0时,二次方程ax2+bx+c=0有两个不等的实数根x1,x2,(设x1
大于在两边,小于在中间。(2)当△=0时,通过配方得, 由图可知,ax2+bx+c>0的解集是 的全体实数,即
ax2+bx+c<0的解集是空集,即不等式无解。(3)当△<0时,二次函数f(x)=ax2+bx+c的图象在x轴上方,由此可知,不等式ax2+bx+c>0的解集是实数集R,不等式ax2+bx+c<0的解集是空集。例2.解不等式1-x-4x2>0.解:原不等式化为4x2+x-1<0,
因为△=12-4×4×(-1)>0,
方程4x2+x-1=0的根是所以不等式的解集是 例3.解不等式x2+4x+4>0.解:因为△=42-4×1×4=0,
原不等式化为(x+2)2>0,
所以不等式的解集是{x∈R| x≠-2}.例4.解不等式-2x2+4x-3>0.解:原不等式化为2x2-4x+3<0,
因为2x2-4x+3=2(x-1)2+1>0,
所以原不等式的解集是解:由函数f(x)的解析式有意义得 即 解得 因此1≤x<3,所求函数的定义域是[1,3).
