《函数y=Asin(ωx+φ)的图象》
文档属性
| 名称 | 《函数y=Asin(ωx+φ)的图象》 |

|
|
| 格式 | rar | ||
| 文件大小 | 47.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-30 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
《函数y=Asin(ωx+φ)的图象》说课稿
武夷山一中 葛香珠
尊敬的各位评委、老师:您们好!
很高兴能参加这次教学研讨活动,向各位老师学习。我说课的内容是人教A版数学必修4第一章第五节《函数y=Asin(ωx+φ)的图象》的起始课。下面我根据自己编写的教案,把对本节课的背景分析、教学目标设计、课堂结构设计、教学过程设计、教学媒体设计、教学评价设计、实时评估学生情况等方面的认识作一个说明。
1、背景分析
1.1学习任务分析:
本节课是在学生已经掌握函数y=Asin(ωx+φ) “五点(画图)法”的前提下,通过学生自己作图,自主探究,并在教师的引导下,利用“五点法”考察参数Α、ω、φ的特殊值对函数y=Asin(ωx+φ)的图象的影响,从而学习如何将一个复杂问题分解为若干简单问题的方法,这是本节课的重点。
1.2学生情况分析:
本班(奥赛班)学生思维较为活跃,学习积极性高,动手能力强、已初步具有对数学问题进行独立探究、合作探究的意识与能力。尽管如此,但学生可能较难理解图象变换与函数解析式变换的内在联系,本节课要特别突破的教学难点是:ω对y=Asin(ωx+φ)的图象的影响规律。
2、教学目标设计
知识与技能——能正确说出特殊值φ 、ω( ω >0)、 Α(A>0)对函数y=Asin(ωx+φ)的图象
的影响规律。
过程与方法——通过引导学生对函数图象变换规律的探索,让学生体会到由简单到复杂,特殊
到一般的化归思想。
情感态度与价值观——让学生切身体验数学建模的过程,培养学生合作交流的学习方式,使学生形成主动克服困难的意志品质。
3、课堂结构设计
“问题是数学的心脏”,本节课总体上以学生活动为主线,以问题串的形式,设计为五问一练一设计题。
3.1创设情景,提出问题
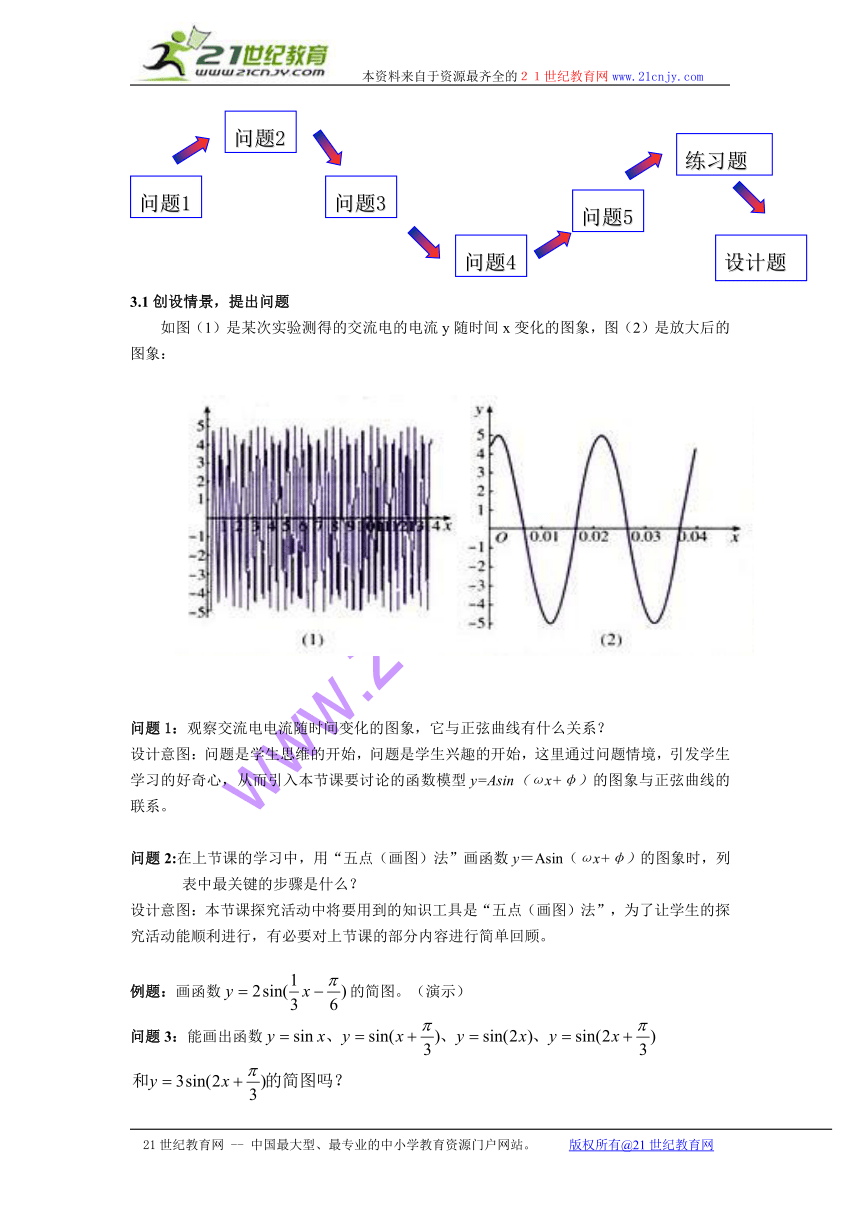
如图(1)是某次实验测得的交流电的电流y随时间x变化的图象,图(2)是放大后的图象:
问题1:观察交流电电流随时间变化的图象,它与正弦曲线有什么关系?
设计意图:问题是学生思维的开始,问题是学生兴趣的开始,这里通过问题情境,引发学生学习的好奇心,从而引入本节课要讨论的函数模型y=Asin(ωx+φ)的图象与正弦曲线的联系。
问题2:在上节课的学习中,用“五点(画图)法”画函数y=Asin(ωx+φ)的图象时,列表中最关键的步骤是什么?
设计意图:本节课探究活动中将要用到的知识工具是“五点(画图)法”,为了让学生的探究活动能顺利进行,有必要对上节课的部分内容进行简单回顾。
例题:画函数的简图。(演示)
问题3:能画出函数
3.2自我尝试、运用方法(问题设计意图:培养学生实践能力及发现问题,解决问题的能力)
问题4:(重点题)
函数的图象可由正弦曲线经过怎样变化得到?
函数的图象可由的图象经过怎样变化得到?
函数的图象可由的图象经过怎样变化得到?
问题5:函数的图象可由正弦曲线经过怎样变化得到?(演示课件1)
变化路径简述:
(1)
如果学生上面变换路径掌握较好,还可以试着让学生阅读与思考下面变换路径错在哪儿?目的是在阅读中引导学生通过图象发现错误,并分析错误原因,使学生自己从错误中走出来,也就巧妙地突破了本节课的教学难点。阅读变化路径示例目的是让学生领略到多种变化路径,拓展思维空间。
阅读与思考:
(2)
设,则
变化路径示例:
(3)
课堂练习:
1、 P55练习: 1.1、 1.4; 2.
2、 P57习题1.5 A组 1.
设计意图:通过练习,及时了解学生对图象变换的掌握情况以调整课堂节奏。
在获得上述探究体验的基础上,为了进一步培养学生自主获得知识,体会数学的研究方法,巩固教学效果,完善认知结构,深化所学知识,设置了以下学生课外个人设计题(要求上交):
3.4自我尝试、深化认识
学生课外个人设计题
类似问题4:
函数的图象可由正弦曲线经过怎样变化得到?
函数的图象可由的图象经过怎样变化得到?
函数的图象可由的图象经过怎样变化得到?
类似问题5:函数的图象可由正弦曲线经过怎样变化得到?
通过以上设计题目,能使学生巩固对新知识的深化理解,并留有一定的弹性空间,培养学生创新及应用能力。同时,使学生学会将具体问题向一般问题化归的方法,并形成完整的知识体系。
4、教学过程设计
为了达到本节课的教学目标,在教学中,我把教学过程分为“提出问题”、“实践操作”、“探索观察”、“知识巩固”四个阶段。下面对每个阶段教学中计划解决的主要问题和教学步骤进行说明。
4.1提出问题阶段:
为激发学生学习的兴趣,创设问题情景,建立函数y=sinx与y=Asin(ωx+φ)图象的联系。本节课,首先通过问题2提问“五点(画图)法”列表中的最关键的步骤及例题的演示,为学生准确使用本节课将要用到的工具提供必要的保障。
4.2实践操作阶段:
这一阶段主要是学生独立完成五个函数的作图,并请五个代表板演作图,主要是加深学生对“五点(画图)法”关键步骤的理解,并为下一环节做铺垫。
4.3探索观察阶段:
这一阶段主要解决的问题:要通过学生的探索与学生的观察、教师的引导,发现φ 、ω( ω >0)、 Α(A>0)对函数y=Asin(ωx+φ)的图象的影响规律。
4.4知识巩固阶段:
主要是巩固本节课内容,并稍加推广,加深学生对知识的理解,达到本节课的教学要求。
5、教学媒体设计
教学手段——使用多媒体辅助教学。在本节课教学过程中,利用教学课件进行演示,直观、生动地揭示图形的变化过程,在为学生提供感性认识的基础上,也可以对所得的结论进行验证、加深对知识的理解,且用多媒体显示问题和例题的题目,能增加课容量及信息量,提高课堂效率 。
6、教学评价设计
本节问题设计源于课本,由浅入深,体现梯度。设置学生熟悉的问题情境以激发学生的学习兴趣,关注学生在学习过程中的感受,体验学生的认识状况及理解程度。
通过学生对问题3、4、5的探究思考,广泛参与研讨以培养学生的自信心、团队精神及合作意识。
问题5中的阅读与思考、欣赏部分可作为备用选讲内容,目的是想让学生灵活掌握图象的变换规律。
课堂练习时,由学生口答结果,通过老师的讲解与点评,纠正学生在解题过程中出现的错误,加深学生对变换的正确理解。
由简单到复杂重过程,由复杂到简单重结论。学生课外个人设计题的配置体现了这种理念。为学生独立思考习惯的培养、探索能力的长进和思维品质的提高打下基础。
7、实时评估学生情况
本节课教学设计,以问题为纽带,以问题为桥梁,充分调动学生观察、动手的积极性去解决问题。这样设计的目的是在有限的课堂教学中突出有效性,并针对学生可能出现以下情况进行了相应的教学设计:如果学生数学基础扎实,且非常活跃,能够配合老师,能积极地参与到作图及问题的讨论中来,那么,按正常步骤完成教学;如果学生不积极作图,或者作图出错,则教师需要进行引导,完成问题的提出;如果课堂沉闷,学生启而不发,则教师提出的问题应提问数学成绩优异者进行分析,完成教学任务。当然学生的情况复杂多变,教师要灵活处理课堂中遇到的问题,及时调整课堂节奏。
8、结束语
总之,在本节课中,根据学生的所学情况,充分发挥学生的主体意识,团队精神,通过教师的指导作用,使学生自主获得知识,体会数学的研究方法,有利于发展学生的思维能力及创新能力。
以上是作为一名青年教师对本节课的一些设想,一定有许多不足之处,请在座的专家、老师批评、指正,谢谢大家!
设计题
问题1
问题2
问题3
问题4
问题5
练习题
学生作图
验证图象
提出问题
横坐标缩短到原来的倍
所有点向左平行
移动 个单位长度长度
纵坐标不变
纵坐标伸长到原来的3倍
横坐标不变
所有点向左平行
横坐标缩短到原来的倍
纵坐标不变
移动 个单位长度
纵坐标伸长到原来的3倍
横坐标不变
所有点向左平行
移动 个单位长度
所有点向左平行
纵坐标伸长到原来的3倍
横坐标不变
移动 个单位长度
横坐标缩短到原来的倍倍
纵坐标不变
Φ对y=sin(x+φ)的图象影响
响
ω(ω>0 )对y=sin(ωx+φ)的图象影响
A(A>0)对y=Asin(ωx+φ) 的图象影响
A(A>0),ω(ω>0 ),φ对图象的综合影响
阅读课本P49-53页
总结一般性结论
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
《函数y=Asin(ωx+φ)的图象》说课稿
武夷山一中 葛香珠
尊敬的各位评委、老师:您们好!
很高兴能参加这次教学研讨活动,向各位老师学习。我说课的内容是人教A版数学必修4第一章第五节《函数y=Asin(ωx+φ)的图象》的起始课。下面我根据自己编写的教案,把对本节课的背景分析、教学目标设计、课堂结构设计、教学过程设计、教学媒体设计、教学评价设计、实时评估学生情况等方面的认识作一个说明。
1、背景分析
1.1学习任务分析:
本节课是在学生已经掌握函数y=Asin(ωx+φ) “五点(画图)法”的前提下,通过学生自己作图,自主探究,并在教师的引导下,利用“五点法”考察参数Α、ω、φ的特殊值对函数y=Asin(ωx+φ)的图象的影响,从而学习如何将一个复杂问题分解为若干简单问题的方法,这是本节课的重点。
1.2学生情况分析:
本班(奥赛班)学生思维较为活跃,学习积极性高,动手能力强、已初步具有对数学问题进行独立探究、合作探究的意识与能力。尽管如此,但学生可能较难理解图象变换与函数解析式变换的内在联系,本节课要特别突破的教学难点是:ω对y=Asin(ωx+φ)的图象的影响规律。
2、教学目标设计
知识与技能——能正确说出特殊值φ 、ω( ω >0)、 Α(A>0)对函数y=Asin(ωx+φ)的图象
的影响规律。
过程与方法——通过引导学生对函数图象变换规律的探索,让学生体会到由简单到复杂,特殊
到一般的化归思想。
情感态度与价值观——让学生切身体验数学建模的过程,培养学生合作交流的学习方式,使学生形成主动克服困难的意志品质。
3、课堂结构设计
“问题是数学的心脏”,本节课总体上以学生活动为主线,以问题串的形式,设计为五问一练一设计题。
3.1创设情景,提出问题
如图(1)是某次实验测得的交流电的电流y随时间x变化的图象,图(2)是放大后的图象:
问题1:观察交流电电流随时间变化的图象,它与正弦曲线有什么关系?
设计意图:问题是学生思维的开始,问题是学生兴趣的开始,这里通过问题情境,引发学生学习的好奇心,从而引入本节课要讨论的函数模型y=Asin(ωx+φ)的图象与正弦曲线的联系。
问题2:在上节课的学习中,用“五点(画图)法”画函数y=Asin(ωx+φ)的图象时,列表中最关键的步骤是什么?
设计意图:本节课探究活动中将要用到的知识工具是“五点(画图)法”,为了让学生的探究活动能顺利进行,有必要对上节课的部分内容进行简单回顾。
例题:画函数的简图。(演示)
问题3:能画出函数
3.2自我尝试、运用方法(问题设计意图:培养学生实践能力及发现问题,解决问题的能力)
问题4:(重点题)
函数的图象可由正弦曲线经过怎样变化得到?
函数的图象可由的图象经过怎样变化得到?
函数的图象可由的图象经过怎样变化得到?
问题5:函数的图象可由正弦曲线经过怎样变化得到?(演示课件1)
变化路径简述:
(1)
如果学生上面变换路径掌握较好,还可以试着让学生阅读与思考下面变换路径错在哪儿?目的是在阅读中引导学生通过图象发现错误,并分析错误原因,使学生自己从错误中走出来,也就巧妙地突破了本节课的教学难点。阅读变化路径示例目的是让学生领略到多种变化路径,拓展思维空间。
阅读与思考:
(2)
设,则
变化路径示例:
(3)
课堂练习:
1、 P55练习: 1.1、 1.4; 2.
2、 P57习题1.5 A组 1.
设计意图:通过练习,及时了解学生对图象变换的掌握情况以调整课堂节奏。
在获得上述探究体验的基础上,为了进一步培养学生自主获得知识,体会数学的研究方法,巩固教学效果,完善认知结构,深化所学知识,设置了以下学生课外个人设计题(要求上交):
3.4自我尝试、深化认识
学生课外个人设计题
类似问题4:
函数的图象可由正弦曲线经过怎样变化得到?
函数的图象可由的图象经过怎样变化得到?
函数的图象可由的图象经过怎样变化得到?
类似问题5:函数的图象可由正弦曲线经过怎样变化得到?
通过以上设计题目,能使学生巩固对新知识的深化理解,并留有一定的弹性空间,培养学生创新及应用能力。同时,使学生学会将具体问题向一般问题化归的方法,并形成完整的知识体系。
4、教学过程设计
为了达到本节课的教学目标,在教学中,我把教学过程分为“提出问题”、“实践操作”、“探索观察”、“知识巩固”四个阶段。下面对每个阶段教学中计划解决的主要问题和教学步骤进行说明。
4.1提出问题阶段:
为激发学生学习的兴趣,创设问题情景,建立函数y=sinx与y=Asin(ωx+φ)图象的联系。本节课,首先通过问题2提问“五点(画图)法”列表中的最关键的步骤及例题的演示,为学生准确使用本节课将要用到的工具提供必要的保障。
4.2实践操作阶段:
这一阶段主要是学生独立完成五个函数的作图,并请五个代表板演作图,主要是加深学生对“五点(画图)法”关键步骤的理解,并为下一环节做铺垫。
4.3探索观察阶段:
这一阶段主要解决的问题:要通过学生的探索与学生的观察、教师的引导,发现φ 、ω( ω >0)、 Α(A>0)对函数y=Asin(ωx+φ)的图象的影响规律。
4.4知识巩固阶段:
主要是巩固本节课内容,并稍加推广,加深学生对知识的理解,达到本节课的教学要求。
5、教学媒体设计
教学手段——使用多媒体辅助教学。在本节课教学过程中,利用教学课件进行演示,直观、生动地揭示图形的变化过程,在为学生提供感性认识的基础上,也可以对所得的结论进行验证、加深对知识的理解,且用多媒体显示问题和例题的题目,能增加课容量及信息量,提高课堂效率 。
6、教学评价设计
本节问题设计源于课本,由浅入深,体现梯度。设置学生熟悉的问题情境以激发学生的学习兴趣,关注学生在学习过程中的感受,体验学生的认识状况及理解程度。
通过学生对问题3、4、5的探究思考,广泛参与研讨以培养学生的自信心、团队精神及合作意识。
问题5中的阅读与思考、欣赏部分可作为备用选讲内容,目的是想让学生灵活掌握图象的变换规律。
课堂练习时,由学生口答结果,通过老师的讲解与点评,纠正学生在解题过程中出现的错误,加深学生对变换的正确理解。
由简单到复杂重过程,由复杂到简单重结论。学生课外个人设计题的配置体现了这种理念。为学生独立思考习惯的培养、探索能力的长进和思维品质的提高打下基础。
7、实时评估学生情况
本节课教学设计,以问题为纽带,以问题为桥梁,充分调动学生观察、动手的积极性去解决问题。这样设计的目的是在有限的课堂教学中突出有效性,并针对学生可能出现以下情况进行了相应的教学设计:如果学生数学基础扎实,且非常活跃,能够配合老师,能积极地参与到作图及问题的讨论中来,那么,按正常步骤完成教学;如果学生不积极作图,或者作图出错,则教师需要进行引导,完成问题的提出;如果课堂沉闷,学生启而不发,则教师提出的问题应提问数学成绩优异者进行分析,完成教学任务。当然学生的情况复杂多变,教师要灵活处理课堂中遇到的问题,及时调整课堂节奏。
8、结束语
总之,在本节课中,根据学生的所学情况,充分发挥学生的主体意识,团队精神,通过教师的指导作用,使学生自主获得知识,体会数学的研究方法,有利于发展学生的思维能力及创新能力。
以上是作为一名青年教师对本节课的一些设想,一定有许多不足之处,请在座的专家、老师批评、指正,谢谢大家!
设计题
问题1
问题2
问题3
问题4
问题5
练习题
学生作图
验证图象
提出问题
横坐标缩短到原来的倍
所有点向左平行
移动 个单位长度长度
纵坐标不变
纵坐标伸长到原来的3倍
横坐标不变
所有点向左平行
横坐标缩短到原来的倍
纵坐标不变
移动 个单位长度
纵坐标伸长到原来的3倍
横坐标不变
所有点向左平行
移动 个单位长度
所有点向左平行
纵坐标伸长到原来的3倍
横坐标不变
移动 个单位长度
横坐标缩短到原来的倍倍
纵坐标不变
Φ对y=sin(x+φ)的图象影响
响
ω(ω>0 )对y=sin(ωx+φ)的图象影响
A(A>0)对y=Asin(ωx+φ) 的图象影响
A(A>0),ω(ω>0 ),φ对图象的综合影响
阅读课本P49-53页
总结一般性结论
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
