等比数列前n项的和
图片预览





文档简介
课件21张PPT。等比数列的前n项和福建省同安第一中学方荣报教材分析内容、地位和作用 本课时的学习对象问题启发 类比发现 合作探究三维目标 教学创新 教学程序 创设情境
提出问题
(3分钟) 启发思考
自主探究
(6分钟) 类比联想
解决问题
(7分钟) 作业引疑
实践创新
(3分钟) 梳理知识
构建网络
(5分钟) 合作学习
延伸拓展
(6分钟) 知识巩固
快乐应用
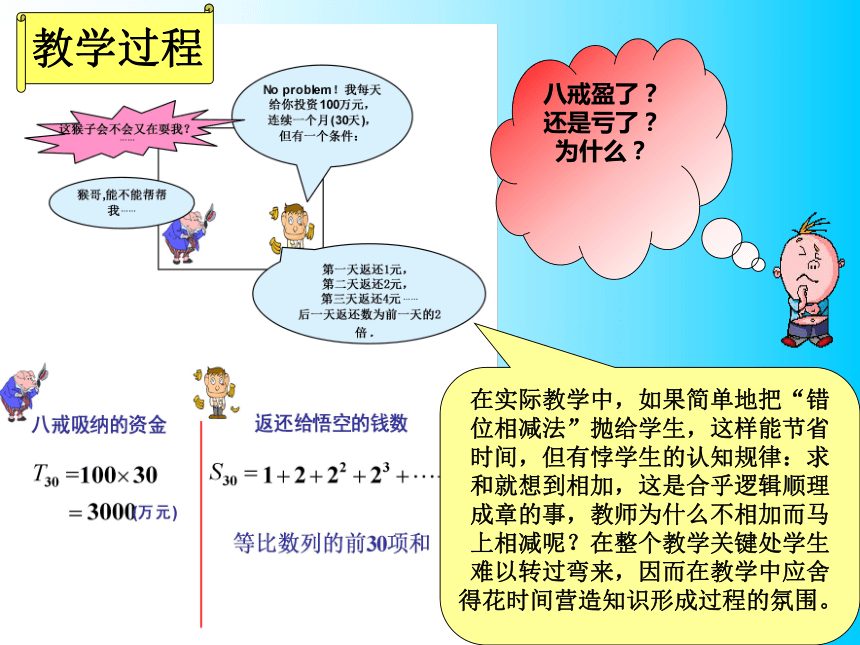
(15分钟) 话说猪八戒自西天取经回到了高老庄,从高员外手里接下了高老庄集团,摇身变成了CEO.可好景不长,高老庄集团因资金周转不灵而陷入了窘境,急需大量资金投入,八戒于是找孙悟空帮忙.悟空一口答应:“行!我每天投资100万元,连续一个月(30天),但是有一个条件是:作为回报,从投资的第一天起你必须返还给我1元,第二天返还2元,第三天返还4元……即后一天返还数为前一天的2倍.”八戒听了,心里打起了小算盘:“第一天:支出1元,收入100万;第二天:支出2元,收入100万,第三天:支出4元,收入100万元;……哇,发财了……” 心里越想越美……再看看悟空的表情,心里又嘀咕了:“这猴子老是欺负我,会不会又在耍我?”西游记后传
教学过程 =?在实际教学中,如果简单地把“错位相减法”抛给学生,这样能节省时间,但有悖学生的认知规律:求和就想到相加,这是合乎逻辑顺理成章的事,教师为什么不相加而马上相减呢?在整个教学关键处学生难以转过弯来,因而在教学中应舍得花时间营造知识形成过程的氛围。教学过程 1,2,22,…,229是什么数列?
有何特征?应归结为什么样的数学问题呢? 探究1 继续探究:
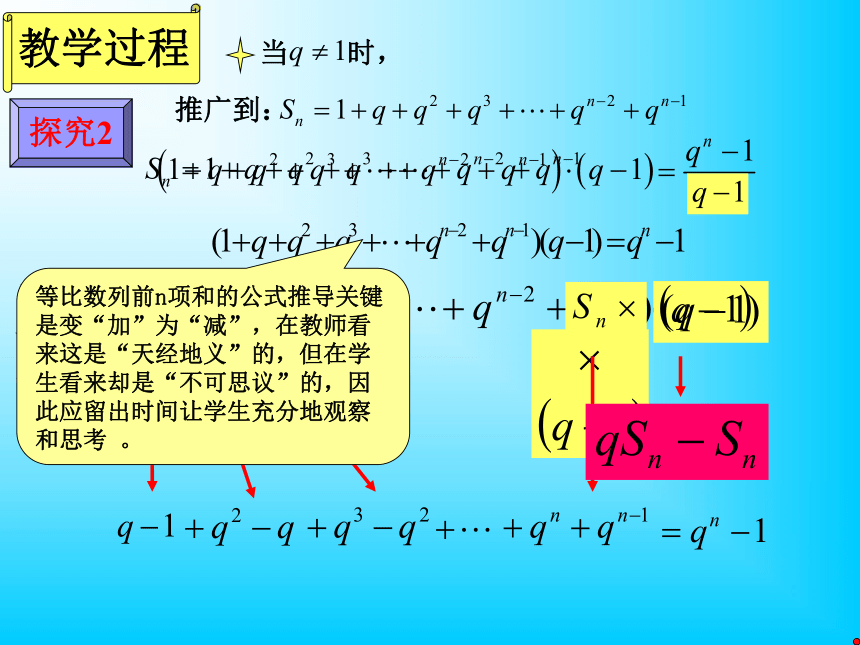
你能猜想数列1,3,32,…,329的前n项和公式吗? 你能猜想数列1,4,42,…,429的前n项和公式吗?教学过程 探究2 教学过程 探究2 观察式子
突破难点等比数列前n项和的公式推导关键是变“加”为“减”,在教师看来这是“天经地义”的,但在学生看来却是“不可思议”的,因此应留出时间让学生充分地观察和思考 。教学过程 倒序相加法等差数列前n项和特殊数列等比数列如何构造特殊数列在教师的指导下,让学生从特殊到一般,从已知到未知,步步深入,让学生自己探究公式,从而体验到学习的愉快和成就感.引导学生观察式子,发现规律,寻找解决问题的技巧,养成善于观察思考的习惯.教学过程 学生自主完成前n项和Sn的推导? 注意讨论教学过程 如何用a1 ,an ,q来表示Sn?解决课前提出的问题:再帮八戒算一下,亏了还是盈了?通过反问精讲,一方面使学生加深对知识的认识,完善知识结构,另一方面使学生由简单地模仿和接受,变为对知识的主动认识,从而进一步提高分析、类比和综合的能力.同时,运用公式解决课前的情景问题,让学生感受到是在“学习有用的数学”.错位相减法提取公比q累加法……教学过程 等比性质你还能用哪些方法求等比数列的激发学生的探索欲望,营造一个让学生主动观察、思考、讨论、互助的氛围.通过小组代表竞争回答,教师及时处理课堂上出现的知识理解或其它问题.通过互动,使师生、生生的交流更加和谐.使学习更为主动,气氛更为热烈.学生的体会是多方位的,多角度的.通过交流和协作,可以相互启发,从而不断完善自己的认知结构.讨论过程中,学生可能无法及时进入状态,老师该怎么操作呢?我觉得可以从以下几个方面入手。一是指导方法,二是语言提醒,三是行动感染。教学过程 例1、判断是非: 例一是让学生巩固公式中的基本量及结构特征,识记公式,引导学生注意q的分类和项数的准确,培养学生思维的严谨性.
教学过程 变式训练:的前多少项的和是 求等比数列等比数列,求第5项到第10项的和; 前n项和数公式共涉及五个量,已知其中3个量可求
另两个量,由此可编出几类题目?你能把它编出来?④③①②例二采用变式教学设计题组,深化学生对公式的认识和理解,通过直接套用公式、变式运用公式、研究公式特点这三个层次的问题解决,加强了对公式的认识和记忆.设置开放题,让全体学生都参与教学,以此培养学生的参与意识和竞争意识.教学过程 例3、小李往银行存入本金10000元,每月利率为0.225%.试计算1年后的本利和是多少?(按复利计息。复利:上一期的本金与利息在下一期一起生息),如果本利和为S,本金为P,单位时间利率为r,存期为n,那么它们之间的关系是老师解释复利知识,并在上述模式的基础上由学生讨论得出解答过程. (元)
例三是实际生活中的储蓄问题,再一次创设问题情境,把学生的学习兴趣进一步推向高潮,激励学生要敢于迎接挑战、战胜困难,进一步培养学生观察、对比、抽象概括及数学建模的能力.教学过程 ①请同学交流本节课的学习感受,并疏理本节课
的主要内容,教师给于补充.
②请同学分析等差、等比数列求和中“倒序相加法
和“错位相减法”的联系与区别.
③请同学说出自己尚未解决的疑问,供教师及同
学思考、解决.
④小结本节课同学们的配合情况,给予表扬,并
提出新要求.老师通过及时地肯定和鼓励学生的配合,能使学生迫切期待下节课的来临,并为此做好充分的准备.让他们永远喜欢数学.培养学生的口头表达能力,归纳概括能力,同时培养他们善于归纳、总结的习惯.从知识的归纳进一步延伸到思想方法提炼,把数学的学习作为提高学生数学素养和文化水平的有效途径.两种数列的求和公式的推导方法,从数学思想和数学方法上来讲是一致的,但是它们也有差异,即错位的方法不同.正是由于这种差异,教师才有了更大的教学空间.当教师把学生从“倒序相加”的思维定式中引导出来的时候,学生的数学思维的深刻性、广阔性等思维品质就得到了提高,思维能力也就提高了.这样,这节课的认知目标和素质目标就基本上都达到了.能对教学情况进行及时、有效的反馈教学过程 必做:课本第61页A组1、2、3题选做:思考题(2)“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,
请问尖头几盏灯?”这首中国古诗的答案是多少?(3)通过本节课的学习,你能用哪些方法求等比数列的前n
项和?有何感受?请写一篇小论文.(4)查阅“芝诺悖论”,并从数列求和的角度加以解释.
(参考网站:http://www.lyge.cn/lygdj/ztwz/shuxue /x2/042.htm)教学过程 等比数列的前n项和设计说明 情
境
设
置
生
活
化 问
题
探
究
活
动
化 作
业
布
置
弹
性
化 思
路
拓
广
数
学
化 巩
固
提
高
梯
度
化 辨
析
质
疑
结
构
化 教学中可能遇到的或学生可能提到的问题多谢大家指导!美丽的同安一中欢迎您!
提出问题
(3分钟) 启发思考
自主探究
(6分钟) 类比联想
解决问题
(7分钟) 作业引疑
实践创新
(3分钟) 梳理知识
构建网络
(5分钟) 合作学习
延伸拓展
(6分钟) 知识巩固
快乐应用
(15分钟) 话说猪八戒自西天取经回到了高老庄,从高员外手里接下了高老庄集团,摇身变成了CEO.可好景不长,高老庄集团因资金周转不灵而陷入了窘境,急需大量资金投入,八戒于是找孙悟空帮忙.悟空一口答应:“行!我每天投资100万元,连续一个月(30天),但是有一个条件是:作为回报,从投资的第一天起你必须返还给我1元,第二天返还2元,第三天返还4元……即后一天返还数为前一天的2倍.”八戒听了,心里打起了小算盘:“第一天:支出1元,收入100万;第二天:支出2元,收入100万,第三天:支出4元,收入100万元;……哇,发财了……” 心里越想越美……再看看悟空的表情,心里又嘀咕了:“这猴子老是欺负我,会不会又在耍我?”西游记后传
教学过程 =?在实际教学中,如果简单地把“错位相减法”抛给学生,这样能节省时间,但有悖学生的认知规律:求和就想到相加,这是合乎逻辑顺理成章的事,教师为什么不相加而马上相减呢?在整个教学关键处学生难以转过弯来,因而在教学中应舍得花时间营造知识形成过程的氛围。教学过程 1,2,22,…,229是什么数列?
有何特征?应归结为什么样的数学问题呢? 探究1 继续探究:
你能猜想数列1,3,32,…,329的前n项和公式吗? 你能猜想数列1,4,42,…,429的前n项和公式吗?教学过程 探究2 教学过程 探究2 观察式子
突破难点等比数列前n项和的公式推导关键是变“加”为“减”,在教师看来这是“天经地义”的,但在学生看来却是“不可思议”的,因此应留出时间让学生充分地观察和思考 。教学过程 倒序相加法等差数列前n项和特殊数列等比数列如何构造特殊数列在教师的指导下,让学生从特殊到一般,从已知到未知,步步深入,让学生自己探究公式,从而体验到学习的愉快和成就感.引导学生观察式子,发现规律,寻找解决问题的技巧,养成善于观察思考的习惯.教学过程 学生自主完成前n项和Sn的推导? 注意讨论教学过程 如何用a1 ,an ,q来表示Sn?解决课前提出的问题:再帮八戒算一下,亏了还是盈了?通过反问精讲,一方面使学生加深对知识的认识,完善知识结构,另一方面使学生由简单地模仿和接受,变为对知识的主动认识,从而进一步提高分析、类比和综合的能力.同时,运用公式解决课前的情景问题,让学生感受到是在“学习有用的数学”.错位相减法提取公比q累加法……教学过程 等比性质你还能用哪些方法求等比数列的激发学生的探索欲望,营造一个让学生主动观察、思考、讨论、互助的氛围.通过小组代表竞争回答,教师及时处理课堂上出现的知识理解或其它问题.通过互动,使师生、生生的交流更加和谐.使学习更为主动,气氛更为热烈.学生的体会是多方位的,多角度的.通过交流和协作,可以相互启发,从而不断完善自己的认知结构.讨论过程中,学生可能无法及时进入状态,老师该怎么操作呢?我觉得可以从以下几个方面入手。一是指导方法,二是语言提醒,三是行动感染。教学过程 例1、判断是非: 例一是让学生巩固公式中的基本量及结构特征,识记公式,引导学生注意q的分类和项数的准确,培养学生思维的严谨性.
教学过程 变式训练:的前多少项的和是 求等比数列等比数列,求第5项到第10项的和; 前n项和数公式共涉及五个量,已知其中3个量可求
另两个量,由此可编出几类题目?你能把它编出来?④③①②例二采用变式教学设计题组,深化学生对公式的认识和理解,通过直接套用公式、变式运用公式、研究公式特点这三个层次的问题解决,加强了对公式的认识和记忆.设置开放题,让全体学生都参与教学,以此培养学生的参与意识和竞争意识.教学过程 例3、小李往银行存入本金10000元,每月利率为0.225%.试计算1年后的本利和是多少?(按复利计息。复利:上一期的本金与利息在下一期一起生息),如果本利和为S,本金为P,单位时间利率为r,存期为n,那么它们之间的关系是老师解释复利知识,并在上述模式的基础上由学生讨论得出解答过程. (元)
例三是实际生活中的储蓄问题,再一次创设问题情境,把学生的学习兴趣进一步推向高潮,激励学生要敢于迎接挑战、战胜困难,进一步培养学生观察、对比、抽象概括及数学建模的能力.教学过程 ①请同学交流本节课的学习感受,并疏理本节课
的主要内容,教师给于补充.
②请同学分析等差、等比数列求和中“倒序相加法
和“错位相减法”的联系与区别.
③请同学说出自己尚未解决的疑问,供教师及同
学思考、解决.
④小结本节课同学们的配合情况,给予表扬,并
提出新要求.老师通过及时地肯定和鼓励学生的配合,能使学生迫切期待下节课的来临,并为此做好充分的准备.让他们永远喜欢数学.培养学生的口头表达能力,归纳概括能力,同时培养他们善于归纳、总结的习惯.从知识的归纳进一步延伸到思想方法提炼,把数学的学习作为提高学生数学素养和文化水平的有效途径.两种数列的求和公式的推导方法,从数学思想和数学方法上来讲是一致的,但是它们也有差异,即错位的方法不同.正是由于这种差异,教师才有了更大的教学空间.当教师把学生从“倒序相加”的思维定式中引导出来的时候,学生的数学思维的深刻性、广阔性等思维品质就得到了提高,思维能力也就提高了.这样,这节课的认知目标和素质目标就基本上都达到了.能对教学情况进行及时、有效的反馈教学过程 必做:课本第61页A组1、2、3题选做:思考题(2)“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,
请问尖头几盏灯?”这首中国古诗的答案是多少?(3)通过本节课的学习,你能用哪些方法求等比数列的前n
项和?有何感受?请写一篇小论文.(4)查阅“芝诺悖论”,并从数列求和的角度加以解释.
(参考网站:http://www.lyge.cn/lygdj/ztwz/shuxue /x2/042.htm)教学过程 等比数列的前n项和设计说明 情
境
设
置
生
活
化 问
题
探
究
活
动
化 作
业
布
置
弹
性
化 思
路
拓
广
数
学
化 巩
固
提
高
梯
度
化 辨
析
质
疑
结
构
化 教学中可能遇到的或学生可能提到的问题多谢大家指导!美丽的同安一中欢迎您!
