空间中直线与直线的位置关系
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
课题:空间中直线与直线的位置关系
漳州三中 李志卿
一、教材分析
1、教材版本及章节
《普通高中课程标准实验教科书·数学2》(人教A版·必修)第二章第2.1.2节《空间中直线与直线的位置关系》
2、教材的地位与作用
必修2的立体几何初步是《普通高中数学课程标准(实验稿)》立体几何教学的第一部分内容,与以往教学立体几何的内容体系相比,本册教科书立体几何的内容体系结构有重大改革:先是从对空间几何体的整体感受入手,再以长方体为载体研究组成空间几何体的点、直线和平面。这种安排有助于发展学生的空间观念、培养学生的空间想象能力、几何直观能力,适当减轻几何论证的难度,降低立体几何学习入门的门槛,提高学生学习立体几何的兴趣。
本节课《2.1.2空间中直线与直线的位置关系》是在平面中两条直线位置关系及平面的基本性质的基础上提出来的。它既是研究空间点、直线、平面之间各种位置关系的开始,又是学习这些位置关系的基础。因此要特别注意有一个好的开始,感性认识空间中两直线的位置关系,使学生逐步养成在空间考虑问题的习惯。
3、教学目标
(1)知识与技能目标:
①经历获取异面直线的概念、异面直线所成的角的概念的过程,并会求简单的异面直线所成的角。
②了解空间两直线的位置关系,培养学生的画图能力和空间想象能力;了解公理4和等角定理,运用它们解决简单问题,进一步培养将空间问题转化为平面问题的能力和逻辑思维能力。
(2)情感与价值目标:
让学生感受到掌握空间两直线关系的必要性,通过“观察”、“ 思考”、“探究”和合理的设问,把问题放给学生,让学生去自主解决,提高学生的学习兴趣,培养学生独立学习的习惯。
4、教学重点和难点
重点:异面直线的概念、异面直线所成的角的概念和简单的异面直线所成的角的求法。
难点:异面直线的概念的理解、异面直线所成的角的概念和求法。
5、教学用具
三角板、两把圆规和多媒体课件
二、学情分析和学法指导
1、学情分析
空间直线的位置关系在现实生活中大量存在,学生对它们已有一定的感性认识。其中,相交直线和平行直线都是共面直线,学生对它们已很熟悉。异面直线的概念是学生比较生疏的,也是本节的重点和难点,因此,本节重点围绕异面直线的概念和所成的角展开教学。
2、学法指导
高一的学生,其思维仍属于经验型的逻辑思维,很大程度上仍需要依赖具体形象的经验材料来理解抽象的逻辑关系,本节以长方体和具体实物为载体,感性认知两条直线的异面关系。由于本节课的内容多、难点多,学生课前要做好充分的预习工作,通过阅读教材、类比联想、思考与教师交流、概括,从而较好地完成本节课的教学目标。
三、教法分析和教学手段
1、 教法分析
基于新课标的理念,在教学过程中始终落实“三主教学法”:教师主导、学生主体、思维主线,充分利用学生已有的知识让学生积极主动地去建构新知。按照“教师设计合理有序、符合学情的问题→教学过程中提出问题→学生思考(教学进度要随学生的思维情况而定,学生有疑难时要适度启发,但要有度)→师生一起得出结论”的方式师生共同完成教学任务。因此,在定义和定理的引入阶段,我采用观察发现、启发引导、探索讨论相结合的教学方法;在例题讲解、学生练习阶段,以启发、引导、讲授为主。
2、 教学手段
辅助使用多媒体和圆规辅助教学,使书本的图形“动”起来,加强了教学的直观性。
四、教学基本流程
五、教学设计
(一)引入
问题:我们已经研究了平面内两条直线的位置关系,那么空间两条直线有何关系呢
(几何画板演示两条直线的运动而引起的不同位置关系)
【设计意图】由平面引入到空间,自然中的必然,学生易于接受;再利用课件演示两条直线运
动得出既不相交也不平行的情形,说明事物事变化运动的,培养学生在空间考虑问题的习惯,也为异面直线所成的角的求法做好铺垫。
【师生活动】①教师利用几何画板让两条直线运动,学生观察得出既不相交也不平行的情形;
②教师引导学生观察身边的实例如教室(教室可以抽象成为一个长方体)
(二)异面直线的概念
1、由上述的演示和观察得出异面直线的概念 ,师生共同总结空间两条直线位置关系(板书)
【设计意图】:在学生获得空间两条直线存在”既不相交也不平行”的位置关系的直观感知后,以长方体(教室可以抽象成为一个长方体)为载体,引出异面直线的概念,并以“共面”和“异面”为标准,将空间直线分成两类。目的是使空间两直线的位置关系与平面中两直线的位置关系相协调,特别使空间中两直线平行与平面上两直线平行的意义保持一致。
【师生活动】始终强调异面直线指的是不同在任何一个平面内的两条直线,即不相交也不平行。
2、 进一步明晰异面直线的概念
【设计意图】异面直线的概念是本小节的重点和难点,通过问题的设计,教师的启发、概括,让学生正确理解异面直线的概念。
【师生活动】1、判断下列命题是否正确:
①若两条直线没有公共点,则这两条直线互相平行。(× )
②没有公共点的两条直线是异面直线。( × )
③分别位于两个不同平面的两条直线是异面直线。( × )
④某一平面内的一条直线和这个平面外的一条直线是异面直线。( × )
⑤过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线。( √ )
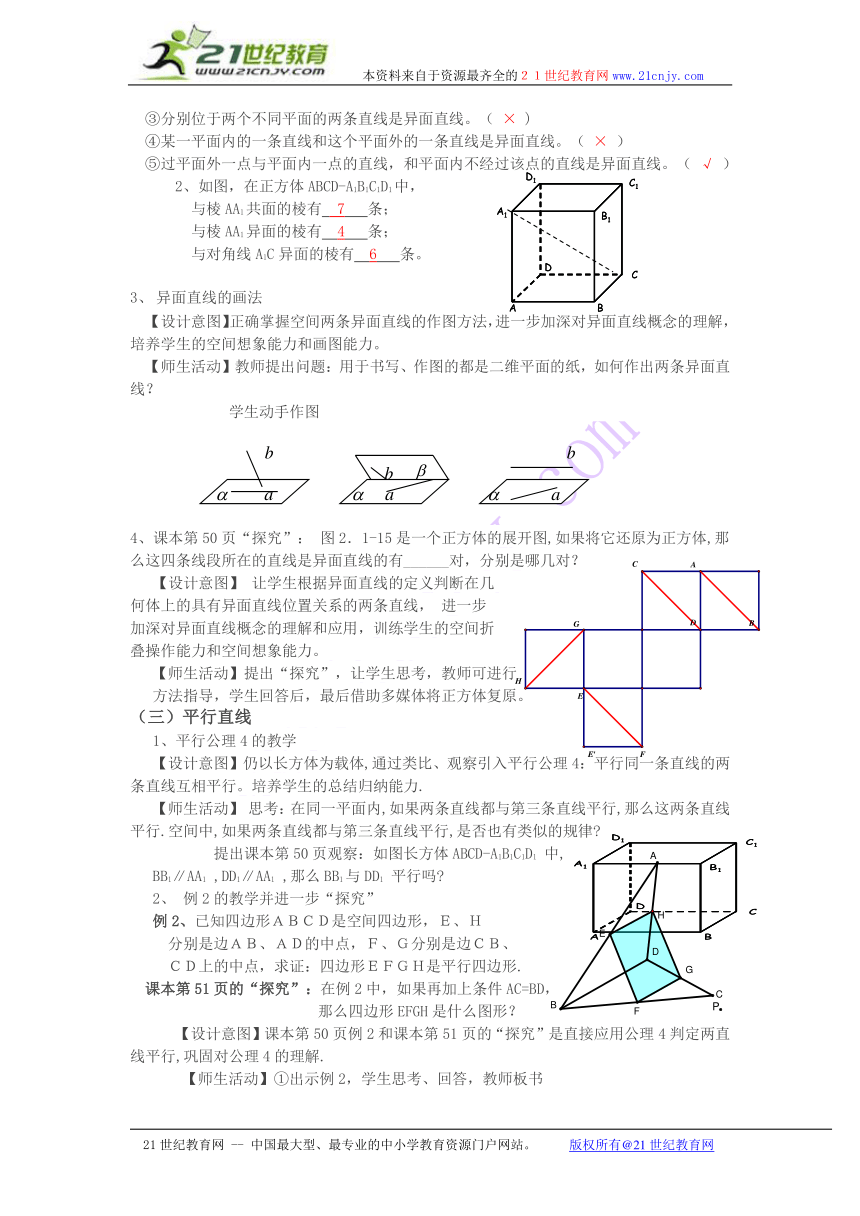
2、如图,在正方体ABCD-A1B1C1D1中,
与棱AA1共面的棱有 7 条;
与棱AA1异面的棱有 4 条;
与对角线A1C异面的棱有 6 条。
3、 异面直线的画法
【设计意图】正确掌握空间两条异面直线的作图方法,进一步加深对异面直线概念的理解,培养学生的空间想象能力和画图能力。
【师生活动】教师提出问题:用于书写、作图的都是二维平面的纸,如何作出两条异面直线?
学生动手作图
4、课本第50页“探究”: 图2.1-15是一个正方体的展开图,如果将它还原为正方体,那么这四条线段所在的直线是异面直线的有______对,分别是哪几对?
【设计意图】 让学生根据异面直线的定义判断在几
何体上的具有异面直线位置关系的两条直线, 进一步
加深对异面直线概念的理解和应用,训练学生的空间折
叠操作能力和空间想象能力。
【师生活动】提出“探究”,让学生思考,教师可进行
方法指导,学生回答后,最后借助多媒体将正方体复原。
(三)平行直线
1、平行公理4的教学
【设计意图】仍以长方体为载体,通过类比、观察引入平行公理4:平行同一条直线的两条直线互相平行。培养学生的总结归纳能力.
【师生活动】 思考:在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线平行.空间中,如果两条直线都与第三条直线平行,是否也有类似的规律
提出课本第50页观察:如图长方体ABCD-A1B1C1D1 中,
BB1∥AA1 ,DD1∥AA1 ,那么BB1与DD1 平行吗
2、 例2的教学并进一步“探究”
例2、已知四边形ABCD是空间四边形,E、H
分别是边AB、AD的中点,F、G分别是边CB、
CD上的中点,求证:四边形EFGH是平行四边形.
课本第51页的“探究”:在例2中,如果再加上条件AC=BD,
那么四边形EFGH是什么图形?
【设计意图】课本第50页例2和课本第51页的“探究”是直接应用公理4判定两直线平行,巩固对公理4的理解.
【师生活动】①出示例2,学生思考、回答,教师板书
②出示第51页的“探究”,可以找一位学生上台板演,其余学生独立完成,根据学生完成情况教师总结解决空间问题的一般思维方法:空间图形转化成平面图形,然后利用利用平面几何的知识解决。
(四)异面直线所成的角
1、等角定理的教学
【设计意图】初中平面几何的等角定理已删除,故先提出平面等角定理,以思考开始,进而提出把等角问题推广到空间是否成立,引发学生的思考和探索。为了使学生形成直观认识,先引导学生观察两个圆规演示,最终领会空间中的等角定理,为下一步讲一面直线所成的角打下基础。
【师生活动】①提出思考:在平面上,我们容易证明“如果一个角的两边和另外一个角的两边分别平行,那么这两个角相等或互补”.空间中是否仍然成立呢 观察上述长方体中的∠ADC 与∠A1D1C1 , ∠ADC与∠A1B1C1 大小关系如何
②教师利用两个圆规演示等角定理
2、如何刻画两条异面直线所成的角?
【设计意图】 异面直线所成的角是由两条相交直线直线所成的角扩充而生成的.通过让同学们动手画平行线的方式,使两条异面直线移到同一平面的位置上,把立体图形的问题转化为平面图形的问题,使学生认真体会.
【师生活动】①由平面内相交直线的夹角引出异面直线所成的角的概念。
②提出思考:两异面直线所成的角的大小与点O 有关吗 (无关)
③总结作异面直线所成的角方法和线线垂直的定义
3、课本第52页的“探究”和例3的教学
第52页的“探究”:
(1)如图2.1-20,观察长方体 ,有没有两条棱所在的直线是互相垂直的异面直线
(2)如果两条平行直线中的一条与某一条直线垂直,那么,另一条直线是否也与这条直线垂直
(3)垂直于同一条直线的两条直线是否平行
例3、如图,正方体ABCD-A1B1C1D1中,
(1)哪些棱所在直线与直线BA1是异面直线?
(2)直线BA1 和CC1的夹角是多少?
(3)哪些棱所在直线与直线AA1垂直?
【设计意图】 以学生熟知的长方体和正方体为载体,使学生在直观感知的基础上,认识空间中一般的直线与直线的位置关系,使学生初步掌握依据定义、定理对空间图形进行推理论证、计算的方法.
【师生活动】教师启发,学生思考回答,教师板书例3第(2)小题过程,最后总结求异面直线所成角的一般步骤,强调其关键是通过平移转化为相交直线的夹角。
(五)课堂练习
课本第53页,练习第1、2题
【设计意图】使学生进一步掌握异面直线所成角的定义和求解过程,培养学生将空间问题转化为平面问题的能力。
【师生活动】学生独立解题,教师巡视,个别辅导。
(六) 课堂小结
(1) 什么是平行公理、等角定理以及两条异面直线所成的角
(2) 平行公理的作用是什么 (3) 感性认识空间中两直线的位置关系.
【设计意图】要使学生对所学知识心中有数,培养学生反思的习惯和概括能力。
【师生活动】先由学生讨论,自己归纳整理,然后请1-2个学生代表总结,最后由教师肯定和补充。
(七)作业
(1) P56习题2.1A组3,4⑴⑵⑶,6
(2)补充:如图,在空间四边形ABCD中,AD=BC=2,E、F分别是AB、CD的中点,若EF=,求直线AD与BC所成的角。
(3)探究4:
①在课本第51页的“探究”中,如果再加上条件AC⊥BD,那么四边形EFGH是什么图形?为什么?
②在例2中,把条件“F、G分别是边CB、 CD上的中点”改为“F、G分别是边CB、
CD上的点,且。那么四边形EFGH是什么图形?为什么?
【设计意图】P56习题2.1A组3,4⑴⑵⑶是对基本概念的把握;P56习题2.1A组第6题和补充题是对平行公理和异面直线所成角的进一步巩固,强化基本技能训练和解题规范的初步训练,并以此作为学生对本节内容各项指标的落实评价。探究4引导学生进一步探索,进行变式训练,开拓思维的广度。
五、教学设计说明
新课程数学中,立体几何不论从教材编排还是教学要求上都发生了很大变化,因而,我在本节课的处理上也作了相应调整,借助多媒体辅助教学,采用“引导—探究式”教学方法。整个教学过程遵循“直观感知—操作确认—归纳总结”的认知规律,注重发展学生的合情推理能力,降低几何证明的难度,同时,加强空间观念的培养,注重知识产生的过程性。
1、立体几何实际上与生活的联系非常密切,很多实物都可以看成是各式各样的空间几何体。在这节中,改变了以往教学立体几何的顺序,没有从抽象的概念出发,推导直线的位置关系,而是借助直观具体的实物和长方体模型,让学生通过一系列的实际活动,直观感知、操作确认、思辩论证,认识空间两直线的位置关系。
2、本节课贯彻了教师主导性、学生主体性的新课程理念, 以学生为本,采用启发式教学,根据现代建构主义理论,从思维的最近发展区出发,通过类比法,激活了学生原有的认知规律。
3、问题式教学。问题是创新的关键,在教学中,通过创设问题情境引起学生思考,安排展开图复原,讨论交流,给学生充分活动的时间与空间,帮助学生从自己的实践中获取知识。学生能做的事就让他们自己去做,使学生更好的参与教学活动,展开思维,体验探索的乐趣,增强学习数学的兴趣。
4、爱因斯坦说过“兴趣是最好的老师,它永远胜过责任心”,本节课合理使用多媒体,特别是几何画板强大的动态演示功能,展示两直线的运动、正方体展开图的复原、异面直线所成角的形成过程;利用传统教具——圆规的另类作用展示等角定理,这些都形象直观,激发学生的学习兴趣,引导学生自主学习,自我探索,并从中体会到学习数学的乐趣。
附:板书设计
§2.1.2空间中直线与直线的位置关系一、异面直线的概念:二、两直线的位置关系:异面直线的画法:异面直线所成的角 1、平行公理 2、等角定理 3、异面直线所成的角 例2:证明(板书) 例3(2):解(板书)
类比平面内两直线
位置关系引出课题
观察实物和模型得出
空间直线的位置关系
异面直线的概念、画法
公理4、等角
定理及应用
异面直线所成
的角及求法
课堂
练习
学习小结
与作业
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
课题:空间中直线与直线的位置关系
漳州三中 李志卿
一、教材分析
1、教材版本及章节
《普通高中课程标准实验教科书·数学2》(人教A版·必修)第二章第2.1.2节《空间中直线与直线的位置关系》
2、教材的地位与作用
必修2的立体几何初步是《普通高中数学课程标准(实验稿)》立体几何教学的第一部分内容,与以往教学立体几何的内容体系相比,本册教科书立体几何的内容体系结构有重大改革:先是从对空间几何体的整体感受入手,再以长方体为载体研究组成空间几何体的点、直线和平面。这种安排有助于发展学生的空间观念、培养学生的空间想象能力、几何直观能力,适当减轻几何论证的难度,降低立体几何学习入门的门槛,提高学生学习立体几何的兴趣。
本节课《2.1.2空间中直线与直线的位置关系》是在平面中两条直线位置关系及平面的基本性质的基础上提出来的。它既是研究空间点、直线、平面之间各种位置关系的开始,又是学习这些位置关系的基础。因此要特别注意有一个好的开始,感性认识空间中两直线的位置关系,使学生逐步养成在空间考虑问题的习惯。
3、教学目标
(1)知识与技能目标:
①经历获取异面直线的概念、异面直线所成的角的概念的过程,并会求简单的异面直线所成的角。
②了解空间两直线的位置关系,培养学生的画图能力和空间想象能力;了解公理4和等角定理,运用它们解决简单问题,进一步培养将空间问题转化为平面问题的能力和逻辑思维能力。
(2)情感与价值目标:
让学生感受到掌握空间两直线关系的必要性,通过“观察”、“ 思考”、“探究”和合理的设问,把问题放给学生,让学生去自主解决,提高学生的学习兴趣,培养学生独立学习的习惯。
4、教学重点和难点
重点:异面直线的概念、异面直线所成的角的概念和简单的异面直线所成的角的求法。
难点:异面直线的概念的理解、异面直线所成的角的概念和求法。
5、教学用具
三角板、两把圆规和多媒体课件
二、学情分析和学法指导
1、学情分析
空间直线的位置关系在现实生活中大量存在,学生对它们已有一定的感性认识。其中,相交直线和平行直线都是共面直线,学生对它们已很熟悉。异面直线的概念是学生比较生疏的,也是本节的重点和难点,因此,本节重点围绕异面直线的概念和所成的角展开教学。
2、学法指导
高一的学生,其思维仍属于经验型的逻辑思维,很大程度上仍需要依赖具体形象的经验材料来理解抽象的逻辑关系,本节以长方体和具体实物为载体,感性认知两条直线的异面关系。由于本节课的内容多、难点多,学生课前要做好充分的预习工作,通过阅读教材、类比联想、思考与教师交流、概括,从而较好地完成本节课的教学目标。
三、教法分析和教学手段
1、 教法分析
基于新课标的理念,在教学过程中始终落实“三主教学法”:教师主导、学生主体、思维主线,充分利用学生已有的知识让学生积极主动地去建构新知。按照“教师设计合理有序、符合学情的问题→教学过程中提出问题→学生思考(教学进度要随学生的思维情况而定,学生有疑难时要适度启发,但要有度)→师生一起得出结论”的方式师生共同完成教学任务。因此,在定义和定理的引入阶段,我采用观察发现、启发引导、探索讨论相结合的教学方法;在例题讲解、学生练习阶段,以启发、引导、讲授为主。
2、 教学手段
辅助使用多媒体和圆规辅助教学,使书本的图形“动”起来,加强了教学的直观性。
四、教学基本流程
五、教学设计
(一)引入
问题:我们已经研究了平面内两条直线的位置关系,那么空间两条直线有何关系呢
(几何画板演示两条直线的运动而引起的不同位置关系)
【设计意图】由平面引入到空间,自然中的必然,学生易于接受;再利用课件演示两条直线运
动得出既不相交也不平行的情形,说明事物事变化运动的,培养学生在空间考虑问题的习惯,也为异面直线所成的角的求法做好铺垫。
【师生活动】①教师利用几何画板让两条直线运动,学生观察得出既不相交也不平行的情形;
②教师引导学生观察身边的实例如教室(教室可以抽象成为一个长方体)
(二)异面直线的概念
1、由上述的演示和观察得出异面直线的概念 ,师生共同总结空间两条直线位置关系(板书)
【设计意图】:在学生获得空间两条直线存在”既不相交也不平行”的位置关系的直观感知后,以长方体(教室可以抽象成为一个长方体)为载体,引出异面直线的概念,并以“共面”和“异面”为标准,将空间直线分成两类。目的是使空间两直线的位置关系与平面中两直线的位置关系相协调,特别使空间中两直线平行与平面上两直线平行的意义保持一致。
【师生活动】始终强调异面直线指的是不同在任何一个平面内的两条直线,即不相交也不平行。
2、 进一步明晰异面直线的概念
【设计意图】异面直线的概念是本小节的重点和难点,通过问题的设计,教师的启发、概括,让学生正确理解异面直线的概念。
【师生活动】1、判断下列命题是否正确:
①若两条直线没有公共点,则这两条直线互相平行。(× )
②没有公共点的两条直线是异面直线。( × )
③分别位于两个不同平面的两条直线是异面直线。( × )
④某一平面内的一条直线和这个平面外的一条直线是异面直线。( × )
⑤过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线。( √ )
2、如图,在正方体ABCD-A1B1C1D1中,
与棱AA1共面的棱有 7 条;
与棱AA1异面的棱有 4 条;
与对角线A1C异面的棱有 6 条。
3、 异面直线的画法
【设计意图】正确掌握空间两条异面直线的作图方法,进一步加深对异面直线概念的理解,培养学生的空间想象能力和画图能力。
【师生活动】教师提出问题:用于书写、作图的都是二维平面的纸,如何作出两条异面直线?
学生动手作图
4、课本第50页“探究”: 图2.1-15是一个正方体的展开图,如果将它还原为正方体,那么这四条线段所在的直线是异面直线的有______对,分别是哪几对?
【设计意图】 让学生根据异面直线的定义判断在几
何体上的具有异面直线位置关系的两条直线, 进一步
加深对异面直线概念的理解和应用,训练学生的空间折
叠操作能力和空间想象能力。
【师生活动】提出“探究”,让学生思考,教师可进行
方法指导,学生回答后,最后借助多媒体将正方体复原。
(三)平行直线
1、平行公理4的教学
【设计意图】仍以长方体为载体,通过类比、观察引入平行公理4:平行同一条直线的两条直线互相平行。培养学生的总结归纳能力.
【师生活动】 思考:在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线平行.空间中,如果两条直线都与第三条直线平行,是否也有类似的规律
提出课本第50页观察:如图长方体ABCD-A1B1C1D1 中,
BB1∥AA1 ,DD1∥AA1 ,那么BB1与DD1 平行吗
2、 例2的教学并进一步“探究”
例2、已知四边形ABCD是空间四边形,E、H
分别是边AB、AD的中点,F、G分别是边CB、
CD上的中点,求证:四边形EFGH是平行四边形.
课本第51页的“探究”:在例2中,如果再加上条件AC=BD,
那么四边形EFGH是什么图形?
【设计意图】课本第50页例2和课本第51页的“探究”是直接应用公理4判定两直线平行,巩固对公理4的理解.
【师生活动】①出示例2,学生思考、回答,教师板书
②出示第51页的“探究”,可以找一位学生上台板演,其余学生独立完成,根据学生完成情况教师总结解决空间问题的一般思维方法:空间图形转化成平面图形,然后利用利用平面几何的知识解决。
(四)异面直线所成的角
1、等角定理的教学
【设计意图】初中平面几何的等角定理已删除,故先提出平面等角定理,以思考开始,进而提出把等角问题推广到空间是否成立,引发学生的思考和探索。为了使学生形成直观认识,先引导学生观察两个圆规演示,最终领会空间中的等角定理,为下一步讲一面直线所成的角打下基础。
【师生活动】①提出思考:在平面上,我们容易证明“如果一个角的两边和另外一个角的两边分别平行,那么这两个角相等或互补”.空间中是否仍然成立呢 观察上述长方体中的∠ADC 与∠A1D1C1 , ∠ADC与∠A1B1C1 大小关系如何
②教师利用两个圆规演示等角定理
2、如何刻画两条异面直线所成的角?
【设计意图】 异面直线所成的角是由两条相交直线直线所成的角扩充而生成的.通过让同学们动手画平行线的方式,使两条异面直线移到同一平面的位置上,把立体图形的问题转化为平面图形的问题,使学生认真体会.
【师生活动】①由平面内相交直线的夹角引出异面直线所成的角的概念。
②提出思考:两异面直线所成的角的大小与点O 有关吗 (无关)
③总结作异面直线所成的角方法和线线垂直的定义
3、课本第52页的“探究”和例3的教学
第52页的“探究”:
(1)如图2.1-20,观察长方体 ,有没有两条棱所在的直线是互相垂直的异面直线
(2)如果两条平行直线中的一条与某一条直线垂直,那么,另一条直线是否也与这条直线垂直
(3)垂直于同一条直线的两条直线是否平行
例3、如图,正方体ABCD-A1B1C1D1中,
(1)哪些棱所在直线与直线BA1是异面直线?
(2)直线BA1 和CC1的夹角是多少?
(3)哪些棱所在直线与直线AA1垂直?
【设计意图】 以学生熟知的长方体和正方体为载体,使学生在直观感知的基础上,认识空间中一般的直线与直线的位置关系,使学生初步掌握依据定义、定理对空间图形进行推理论证、计算的方法.
【师生活动】教师启发,学生思考回答,教师板书例3第(2)小题过程,最后总结求异面直线所成角的一般步骤,强调其关键是通过平移转化为相交直线的夹角。
(五)课堂练习
课本第53页,练习第1、2题
【设计意图】使学生进一步掌握异面直线所成角的定义和求解过程,培养学生将空间问题转化为平面问题的能力。
【师生活动】学生独立解题,教师巡视,个别辅导。
(六) 课堂小结
(1) 什么是平行公理、等角定理以及两条异面直线所成的角
(2) 平行公理的作用是什么 (3) 感性认识空间中两直线的位置关系.
【设计意图】要使学生对所学知识心中有数,培养学生反思的习惯和概括能力。
【师生活动】先由学生讨论,自己归纳整理,然后请1-2个学生代表总结,最后由教师肯定和补充。
(七)作业
(1) P56习题2.1A组3,4⑴⑵⑶,6
(2)补充:如图,在空间四边形ABCD中,AD=BC=2,E、F分别是AB、CD的中点,若EF=,求直线AD与BC所成的角。
(3)探究4:
①在课本第51页的“探究”中,如果再加上条件AC⊥BD,那么四边形EFGH是什么图形?为什么?
②在例2中,把条件“F、G分别是边CB、 CD上的中点”改为“F、G分别是边CB、
CD上的点,且。那么四边形EFGH是什么图形?为什么?
【设计意图】P56习题2.1A组3,4⑴⑵⑶是对基本概念的把握;P56习题2.1A组第6题和补充题是对平行公理和异面直线所成角的进一步巩固,强化基本技能训练和解题规范的初步训练,并以此作为学生对本节内容各项指标的落实评价。探究4引导学生进一步探索,进行变式训练,开拓思维的广度。
五、教学设计说明
新课程数学中,立体几何不论从教材编排还是教学要求上都发生了很大变化,因而,我在本节课的处理上也作了相应调整,借助多媒体辅助教学,采用“引导—探究式”教学方法。整个教学过程遵循“直观感知—操作确认—归纳总结”的认知规律,注重发展学生的合情推理能力,降低几何证明的难度,同时,加强空间观念的培养,注重知识产生的过程性。
1、立体几何实际上与生活的联系非常密切,很多实物都可以看成是各式各样的空间几何体。在这节中,改变了以往教学立体几何的顺序,没有从抽象的概念出发,推导直线的位置关系,而是借助直观具体的实物和长方体模型,让学生通过一系列的实际活动,直观感知、操作确认、思辩论证,认识空间两直线的位置关系。
2、本节课贯彻了教师主导性、学生主体性的新课程理念, 以学生为本,采用启发式教学,根据现代建构主义理论,从思维的最近发展区出发,通过类比法,激活了学生原有的认知规律。
3、问题式教学。问题是创新的关键,在教学中,通过创设问题情境引起学生思考,安排展开图复原,讨论交流,给学生充分活动的时间与空间,帮助学生从自己的实践中获取知识。学生能做的事就让他们自己去做,使学生更好的参与教学活动,展开思维,体验探索的乐趣,增强学习数学的兴趣。
4、爱因斯坦说过“兴趣是最好的老师,它永远胜过责任心”,本节课合理使用多媒体,特别是几何画板强大的动态演示功能,展示两直线的运动、正方体展开图的复原、异面直线所成角的形成过程;利用传统教具——圆规的另类作用展示等角定理,这些都形象直观,激发学生的学习兴趣,引导学生自主学习,自我探索,并从中体会到学习数学的乐趣。
附:板书设计
§2.1.2空间中直线与直线的位置关系一、异面直线的概念:二、两直线的位置关系:异面直线的画法:异面直线所成的角 1、平行公理 2、等角定理 3、异面直线所成的角 例2:证明(板书) 例3(2):解(板书)
类比平面内两直线
位置关系引出课题
观察实物和模型得出
空间直线的位置关系
异面直线的概念、画法
公理4、等角
定理及应用
异面直线所成
的角及求法
课堂
练习
学习小结
与作业
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
