等腰三角形(1)
图片预览


文档简介
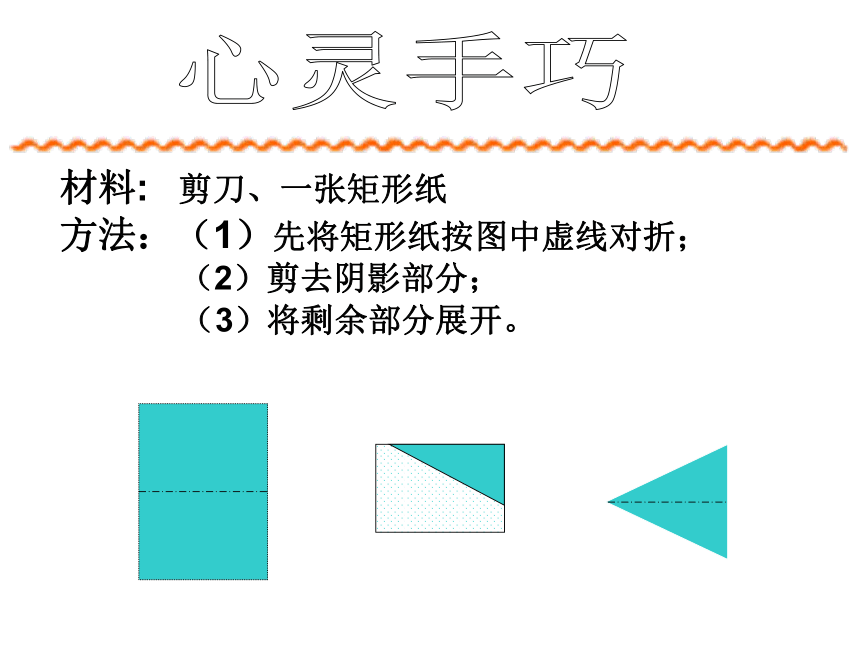
课件20张PPT。12.3.1等腰三角形(1)心灵手巧材料: 剪刀、一张矩形纸方法:(1)先将矩形纸按图中虚线对折;
(2)剪去阴影部分; (3)将剩余部分展开。
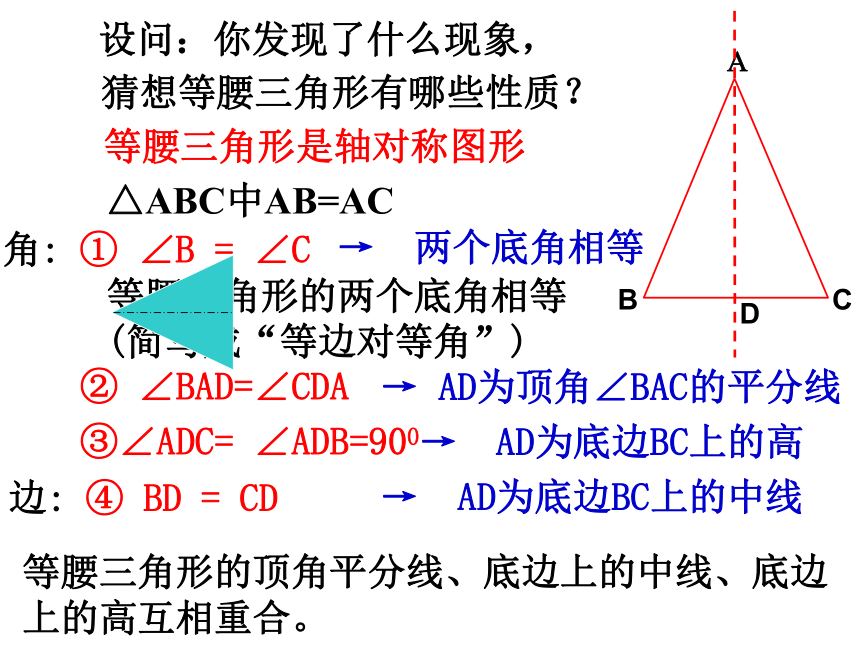
设问:你发现了什么现象, 猜想等腰三角形有哪些性质? 角: ① ∠B = ∠C
② ∠BAD=∠CDA
③∠ADC= ∠ADB=900
边: ④ BD = CD→ AD为顶角∠BAC的平分线
→ AD为底边BC上的高
→ AD为底边BC上的中线
等腰三角形是轴对称图形等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。D→ 两个底角相等等腰三角形的两个底角相等
(简写成“等边对等角”)△ABC中AB=AC 12.3.1等腰三角形
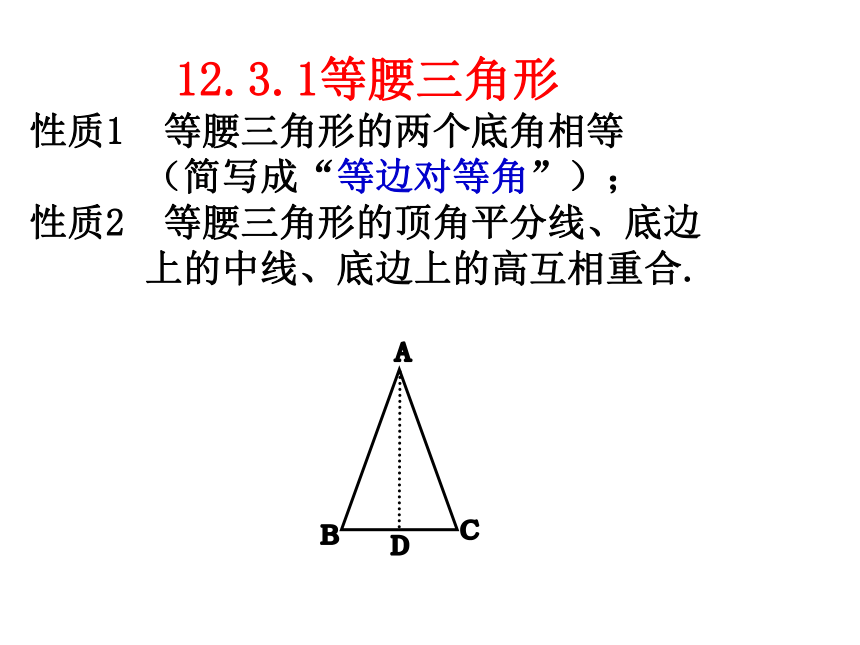
性质1 等腰三角形的两个底角相等
(简写成“等边对等角”);
性质2 等腰三角形的顶角平分线、底边
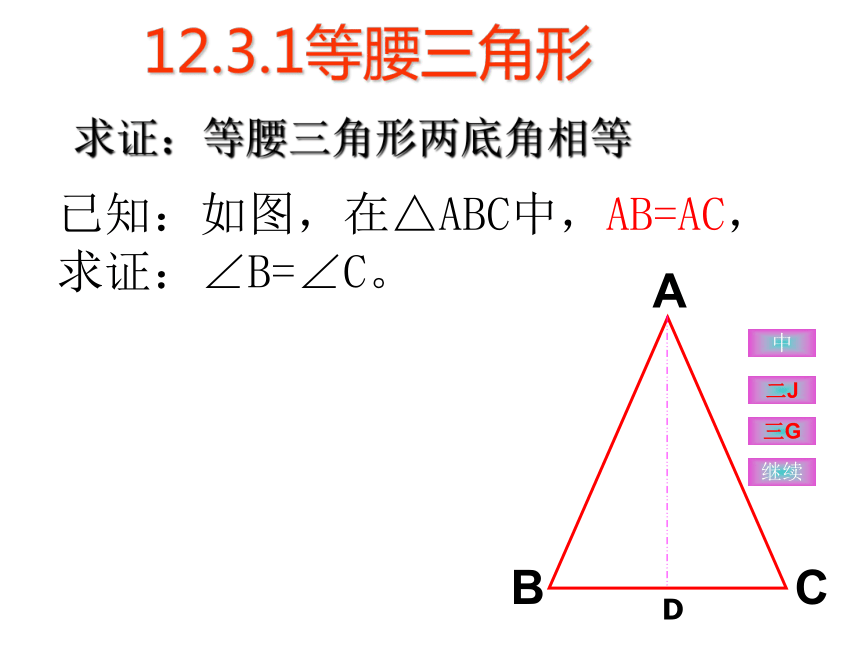
上的中线、底边上的高互相重合. 已知:如图,在△ABC中,AB=AC,
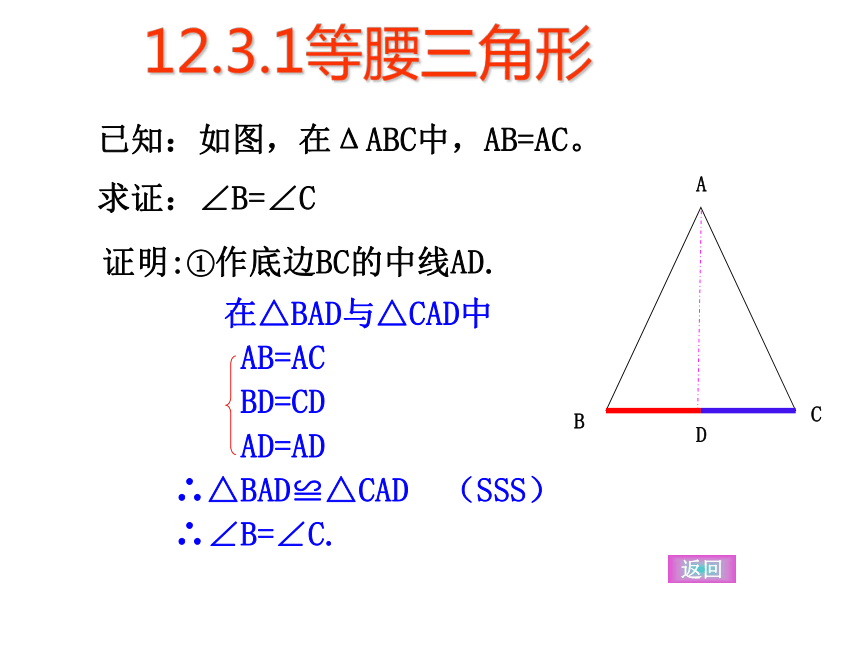
求证:∠B=∠C。 求证:等腰三角形两底角相等12.3.1等腰三角形二J三G中继续D证明:①作底边BC的中线AD.
返回12.3.1等腰三角形D证明:作顶角的平分线AD即∠BAD=∠CAD
在△ABD和△ACD中
AB=AC
∠BAD=∠CAD
AD=AD
∴ △ABD≌ △ACD (SAS)
∴ ∠B= ∠C (全等三角形对应角相等)
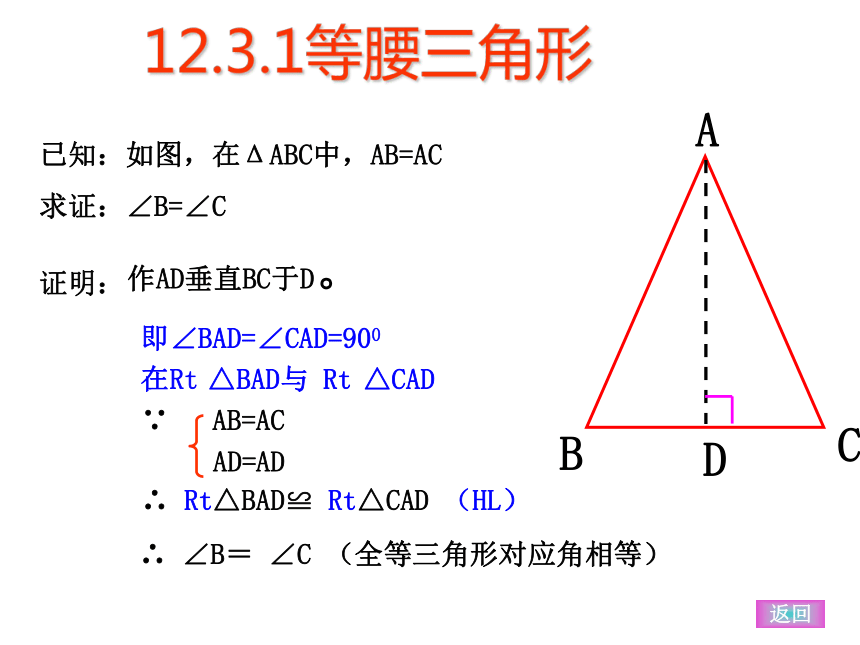
返回12.3.1等腰三角形作AD垂直BC于D。D已知:如图,在ΔABC中,AB=AC
求证:∠B=∠C证明:即∠BAD=∠CAD=900
在Rt △BAD与 Rt △CAD 中
∵ AB=AC
AD=AD
∴ Rt△BAD≌ Rt△CAD (HL)
返回12.3.1等腰三角形∴ ∠B= ∠C (全等三角形对应角相等) 已知:如图,在△ABC中,
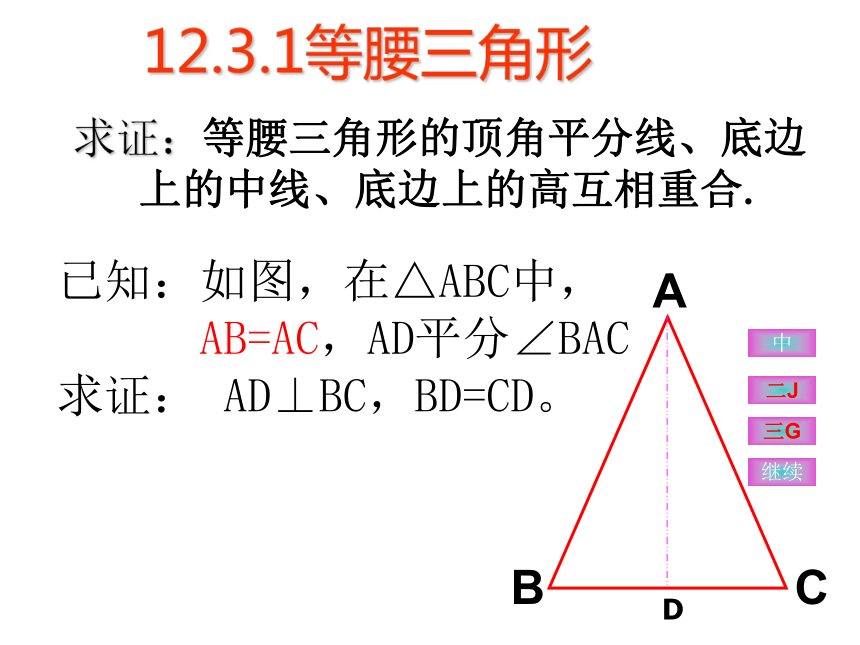
AB=AC,AD平分∠BAC
求证: AD⊥BC,BD=CD。 求证:等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合.二J三G中继续D12.3.1等腰三角形证明:①作底边BC的中线AD.
∴∠BAD=∠CAD ∠ADB=∠ADC
∴ AD平分∠BAD
又∵ ∠ADB+∠ADC =1800
∴∠ADB=∠ADC=900 即AD⊥BC已知:如图,在ΔABC中,AB=AC ,BD=CD 。求证: AD平分∠BAD,AD⊥BC返回在△ABD和△ACD中12.3.1等腰三角形已知:如图,在ΔABC中,AB=AC,AD平分∠BAC求证: BD=CD, AD⊥BC证明:作顶角的平分线AD即∠BAD=∠CAD
在△ABD和△ACD中
AB=AC
∠BAD=∠CAD
AD=AD
∴ △ABD≌ △ACD (SAS)
∴ ∠B= ∠C (全等三角形对应角相等)
返回∵AD平分∠BAC,∴BD=CD ∠ADB=∠ADC
又∵ ∠ADB+∠ADC =1800
∴∠ADB=∠ADC=900 即AD⊥BC
D12.3.1等腰三角形作AD垂直BC于D。D已知:如图,在ΔABC中,AB=AC, AD⊥BC
求证:AD平分∠BAC , BD=CD证明:即∠BAD=∠CAD=900
在Rt △BAD与 Rt △CAD 中
∵ AB=AC
AD=AD
∴ Rt△BAD≌ Rt△CAD (HL)
∴ ∠BAD=∠CAD
BD=CD
返回∵AD⊥BC,∴AD平分∠BAC12.3.1等腰三角形
性质1 等腰三角形的两个底角相等
(简写成“等边对等角”);
性质2 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合.
①在△ABC中, ∵ AB=AC AD平分∠BAC,
∴ ⊥ , ____=_____ ;
②在△ABC中, ∵ AB=AC BD=CD,
∴ ⊥ ,∴ AD平分∠BAC
③在△ABC中, ∵ AB=AC AD⊥BC,
∴∠_____=∠______,_____=_____ .
BAD CADAD BCAD BCBD CDBD CD在△ABC中, ∵ AB=AC ∴ ∠B=?C符号语言12.3.1等腰三角形继续 如图,在下列等腰三角形中,分别求出其它两角的度数。⌒36°⌒ 120° ∟
⌒⌒72 °72 °⌒⌒30 °30 °⌒⌒45°45°用一用练习 1(回答)12.3.1等腰三角形用一用 练习 2(回答)
(1)已知等腰三角形的一个底角是500,
则其余两角为_______________.
(2)已知等腰三角形的一个角是500,
则其余两角为___________________.
(3)已知等腰三角形的一个角是1500,
则其余两角为____________________. 50°,80°或65°,65°15 °,15 °50 °,80°12.3.1等腰三角形 如图,△ABC是等腰直角三角形(AB=AC,∠BAC=90°)。AD是底边BC的高,标出∠B,∠C,∠BAD,∠CAD的度数,图中有哪些相等的线段?ACB∟∟D45°45°45°45°相等的线段:
AB=AC
AD=BD=CD12.3.1等腰三角形返回例如图:在△ABC中,AB=AC,点D在AC上,
且BD=BC=AD.求:△ABC各角的度数。解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,
∠A=∠ABD(等边对等角).
设∠ A=x,则
∠BDC=∠A+∠ABD=2x,
从而 ∠ABC=∠C=∠BDC=2x.
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180°
解得 x=36 °.
在△ABC中, ∠A=36 °, ∠ABC=∠C=72 °.12.3.1等腰三角形变式:在△ABC中,AB=AD=DC,∠BAD=26°,求∠ B 和∠ C的度数。12.3.1等腰三角形
性质1 等腰三角形的两个底角相等
(简写成“等边对等角”);
性质2 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合.
①在△ABC中, ∵ AB=AC AD平分∠BAC,
∴ ⊥ , ____=_____ ;
②在△ABC中, ∵ AB=AC BD=CD,
∴ ⊥ ,∴ AD平分∠BAC
③在△ABC中, ∵ AB=AC AD⊥BC,
∴∠_____=∠______,_____=______ 。
BAD CADAD BCAD BCBD CDBD CD在△ABC中, ∵ AB=AC ∴ ∠B=?C符号语言12.3.1等腰三角形作业12.3.1等腰三角形作业本(2)P11-12
(2)剪去阴影部分; (3)将剩余部分展开。
设问:你发现了什么现象, 猜想等腰三角形有哪些性质? 角: ① ∠B = ∠C
② ∠BAD=∠CDA
③∠ADC= ∠ADB=900
边: ④ BD = CD→ AD为顶角∠BAC的平分线
→ AD为底边BC上的高
→ AD为底边BC上的中线
等腰三角形是轴对称图形等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。D→ 两个底角相等等腰三角形的两个底角相等
(简写成“等边对等角”)△ABC中AB=AC 12.3.1等腰三角形
性质1 等腰三角形的两个底角相等
(简写成“等边对等角”);
性质2 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合. 已知:如图,在△ABC中,AB=AC,
求证:∠B=∠C。 求证:等腰三角形两底角相等12.3.1等腰三角形二J三G中继续D证明:①作底边BC的中线AD.
返回12.3.1等腰三角形D证明:作顶角的平分线AD即∠BAD=∠CAD
在△ABD和△ACD中
AB=AC
∠BAD=∠CAD
AD=AD
∴ △ABD≌ △ACD (SAS)
∴ ∠B= ∠C (全等三角形对应角相等)
返回12.3.1等腰三角形作AD垂直BC于D。D已知:如图,在ΔABC中,AB=AC
求证:∠B=∠C证明:即∠BAD=∠CAD=900
在Rt △BAD与 Rt △CAD 中
∵ AB=AC
AD=AD
∴ Rt△BAD≌ Rt△CAD (HL)
返回12.3.1等腰三角形∴ ∠B= ∠C (全等三角形对应角相等) 已知:如图,在△ABC中,
AB=AC,AD平分∠BAC
求证: AD⊥BC,BD=CD。 求证:等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合.二J三G中继续D12.3.1等腰三角形证明:①作底边BC的中线AD.
∴∠BAD=∠CAD ∠ADB=∠ADC
∴ AD平分∠BAD
又∵ ∠ADB+∠ADC =1800
∴∠ADB=∠ADC=900 即AD⊥BC已知:如图,在ΔABC中,AB=AC ,BD=CD 。求证: AD平分∠BAD,AD⊥BC返回在△ABD和△ACD中12.3.1等腰三角形已知:如图,在ΔABC中,AB=AC,AD平分∠BAC求证: BD=CD, AD⊥BC证明:作顶角的平分线AD即∠BAD=∠CAD
在△ABD和△ACD中
AB=AC
∠BAD=∠CAD
AD=AD
∴ △ABD≌ △ACD (SAS)
∴ ∠B= ∠C (全等三角形对应角相等)
返回∵AD平分∠BAC,∴BD=CD ∠ADB=∠ADC
又∵ ∠ADB+∠ADC =1800
∴∠ADB=∠ADC=900 即AD⊥BC
D12.3.1等腰三角形作AD垂直BC于D。D已知:如图,在ΔABC中,AB=AC, AD⊥BC
求证:AD平分∠BAC , BD=CD证明:即∠BAD=∠CAD=900
在Rt △BAD与 Rt △CAD 中
∵ AB=AC
AD=AD
∴ Rt△BAD≌ Rt△CAD (HL)
∴ ∠BAD=∠CAD
BD=CD
返回∵AD⊥BC,∴AD平分∠BAC12.3.1等腰三角形
性质1 等腰三角形的两个底角相等
(简写成“等边对等角”);
性质2 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合.
①在△ABC中, ∵ AB=AC AD平分∠BAC,
∴ ⊥ , ____=_____ ;
②在△ABC中, ∵ AB=AC BD=CD,
∴ ⊥ ,∴ AD平分∠BAC
③在△ABC中, ∵ AB=AC AD⊥BC,
∴∠_____=∠______,_____=_____ .
BAD CADAD BCAD BCBD CDBD CD在△ABC中, ∵ AB=AC ∴ ∠B=?C符号语言12.3.1等腰三角形继续 如图,在下列等腰三角形中,分别求出其它两角的度数。⌒36°⌒ 120° ∟
⌒⌒72 °72 °⌒⌒30 °30 °⌒⌒45°45°用一用练习 1(回答)12.3.1等腰三角形用一用 练习 2(回答)
(1)已知等腰三角形的一个底角是500,
则其余两角为_______________.
(2)已知等腰三角形的一个角是500,
则其余两角为___________________.
(3)已知等腰三角形的一个角是1500,
则其余两角为____________________. 50°,80°或65°,65°15 °,15 °50 °,80°12.3.1等腰三角形 如图,△ABC是等腰直角三角形(AB=AC,∠BAC=90°)。AD是底边BC的高,标出∠B,∠C,∠BAD,∠CAD的度数,图中有哪些相等的线段?ACB∟∟D45°45°45°45°相等的线段:
AB=AC
AD=BD=CD12.3.1等腰三角形返回例如图:在△ABC中,AB=AC,点D在AC上,
且BD=BC=AD.求:△ABC各角的度数。解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,
∠A=∠ABD(等边对等角).
设∠ A=x,则
∠BDC=∠A+∠ABD=2x,
从而 ∠ABC=∠C=∠BDC=2x.
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180°
解得 x=36 °.
在△ABC中, ∠A=36 °, ∠ABC=∠C=72 °.12.3.1等腰三角形变式:在△ABC中,AB=AD=DC,∠BAD=26°,求∠ B 和∠ C的度数。12.3.1等腰三角形
性质1 等腰三角形的两个底角相等
(简写成“等边对等角”);
性质2 等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合.
①在△ABC中, ∵ AB=AC AD平分∠BAC,
∴ ⊥ , ____=_____ ;
②在△ABC中, ∵ AB=AC BD=CD,
∴ ⊥ ,∴ AD平分∠BAC
③在△ABC中, ∵ AB=AC AD⊥BC,
∴∠_____=∠______,_____=______ 。
BAD CADAD BCAD BCBD CDBD CD在△ABC中, ∵ AB=AC ∴ ∠B=?C符号语言12.3.1等腰三角形作业12.3.1等腰三角形作业本(2)P11-12
