9.1.2 不等式的性质(1)
文档属性
| 名称 | 9.1.2 不等式的性质(1) |  | |
| 格式 | rar | ||
| 文件大小 | 489.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-28 17:42:00 | ||
图片预览


文档简介
课件18张PPT。区五中 牛雷云9.1.2不等式的性质(1)回顾旧知第一组:1+2=3;a+b=b+a;S=ab ;4+x=7
第二组:-7<-5;3+4>1+4;2x<6;a+2>0等式的性质1: 等式两边同时加(或减)同一个数(或式子),结果仍相等。
等式的性质2: 等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。那么不等式有没有类似的性质呢?等式的性质不等式两边都加(或减去)
同一个数
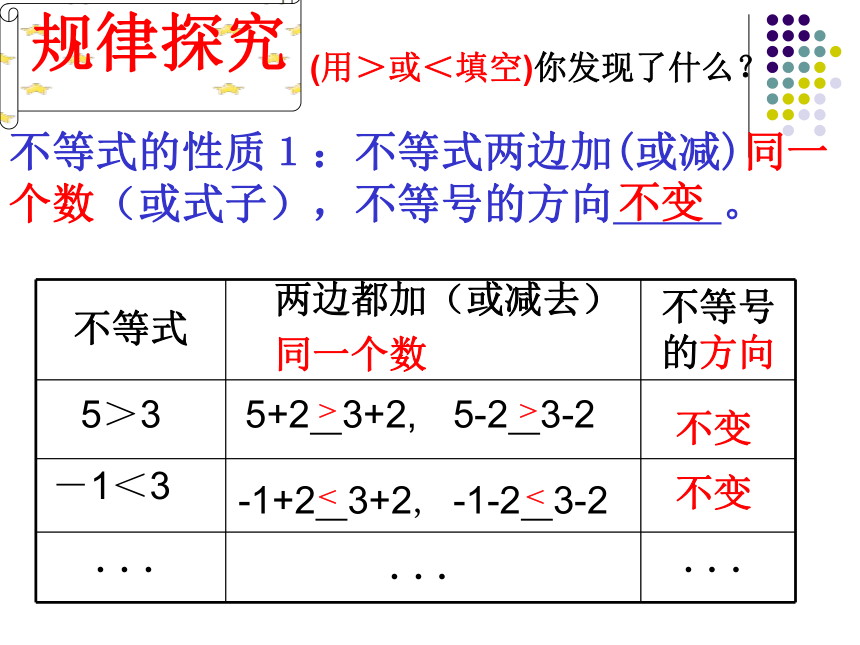
5>3-1<35+2 3+2,5-2 3-2-1+2 3+2,-1-2 3-2不变不变.........不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向 。不变(用>或<填空)你发现了什么?不等号
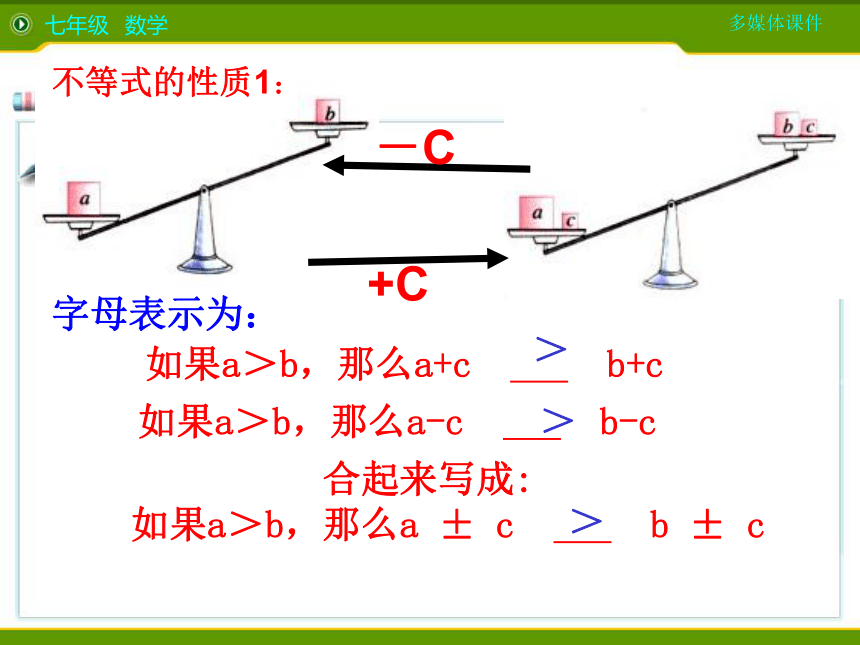
的方向>><<字母表示为:+C-C>如果a>b,那么a-c b-c> 合起来写成:
如果a>b,那么a ± c b ± c>不等式的性质1:如果a>b,那么a+c b+c不等式两边都乘(或除以)
同一个正数
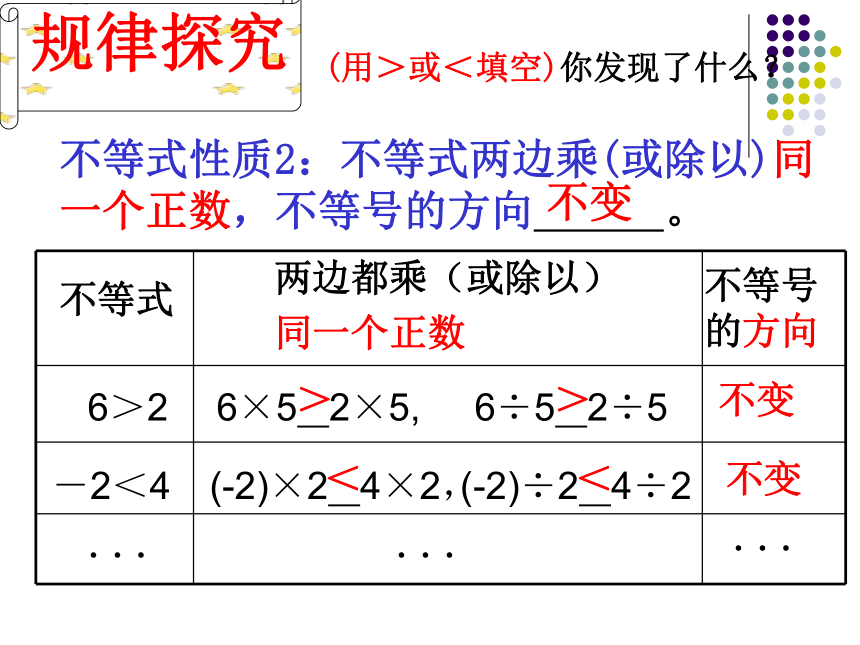
6>26×5 2×5,>不变不变-2<4(-2)÷2 4÷2<.........不等式性质2:不等式两边乘(或除以)同一个正数,不等号的方向 。不变(用>或<填空)你发现了什么?>6÷5 2÷5(-2)×2 4×2,<不等号
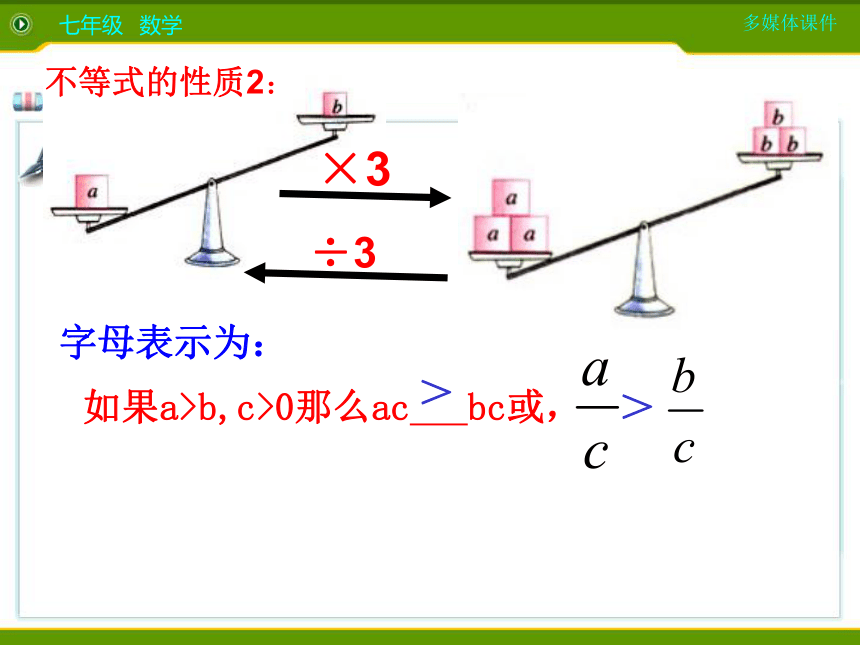
的方向 如果a>b,c>0那么ac bc或,字母表示为:×3÷3 > > 不等式的性质2: 不等式两边都乘(或除以)
同一个负数
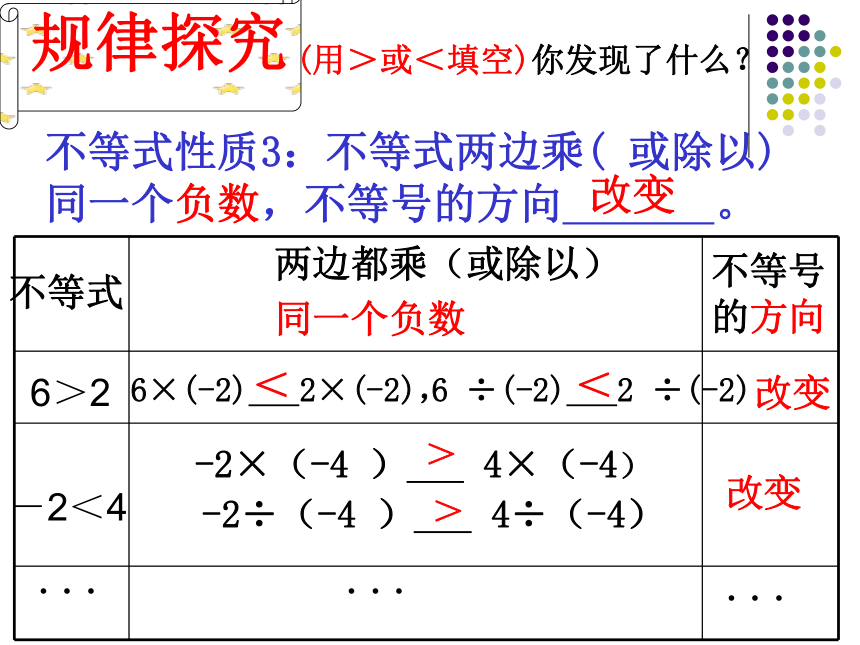
6>26×(-2) 2×(-2),-2<4改变改变.........>改变(用>或<填空)你发现了什么?6 ÷(-2) 2 ÷(-2)><-2÷(-4 ) 4÷(-4)-2×(-4 ) 4×(-4)<不等号
的方向不等式性质3:不等式两边乘( 或除以)同一个负数,不等号的方向 。如果a>b,c<0
那么ac bc,不等式的性质3,也可以用字母表示为:﹤﹤ 不等式的性质与等式的性质有什么相同点、不同点? 设a>b,用不等号连结下列各题中的两式。 (1)a-3 b-3
(2)2a 2b (3)-a -b 设m>n,用“>”或“<”填空:
(1)m-5 n-5(根据不等式的性质 )
(2)1/2m 1/2n (根据不等式的性质 )
(3)-3/2m -3/2n(根据不等式的性质 )
(4)2m-3 2n-3(根据不等式的性质 ) > ><>><231小试牛刀>1、2(1)如果x-5>4,那么两边都加上5,根据不等式的性质 ,可以得到 。
(2)如果 1/2 x < 3,那么两边都乘以2,
根据不等式的性质 ,可得到 。范例学习(3)如果-3x>9,那么两边都除以-3,
根据不等式的性质 ,可得到 。例1填空:x>92x < 63x <- 31回味无穷本节课你的收获是什么? 1、不等式的性质1、2、3 2、将不等式化为:x﹥a 或x﹤a的
形式
3、在数学中注意运用类比的思想 方法 作业:
选做题: P127 习题9.1
第6题
P127习题9.1:第4、5题人之所以能,
是相信能。谢谢指导!例2、利用不等式的性质解下列不等式,并把不等式的解集用数轴表示出来。学 以 致 用(1)(2)方法指导:解不等式时也可以“移项”,请你尝试用“移项”的方法解上述不等式。(1)移项要变号,(2)不等式两边除以同一个负数时,不等号方向要改变。
(1) x-7>26分析:解未知数为x的不等式,就是要使不等式逐步化为x﹥a或x﹤a的形式.
解:(1)为了使不等式x-7>26中不等号的一边变为x,根据不等式的性质1,不等式两边都加7,不等号的方向不变,得
x-7+7﹥26+7
x﹥33
这个不等式的解集在数轴上的表示如图,
锋 芒 初 试 (2) 3x<2x+1 3x-2x﹤2x+1-2x
x﹤1 解:为了使不等式3x<2x+1中不等号的一边变为x,根据 ,不等式两边都减去 ,不等号的方向 ,得这个不等式的解在数轴上的表示如图注意:解不等式时也可以“移项”,即把不等式的一边的某项变号后移到另一边,而不改变不等号的方向.言必有“据”不等式的性质12x不变
第二组:-7<-5;3+4>1+4;2x<6;a+2>0等式的性质1: 等式两边同时加(或减)同一个数(或式子),结果仍相等。
等式的性质2: 等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。那么不等式有没有类似的性质呢?等式的性质不等式两边都加(或减去)
同一个数
5>3-1<35+2 3+2,5-2 3-2-1+2 3+2,-1-2 3-2不变不变.........不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向 。不变(用>或<填空)你发现了什么?不等号
的方向>><<字母表示为:+C-C>如果a>b,那么a-c b-c> 合起来写成:
如果a>b,那么a ± c b ± c>不等式的性质1:如果a>b,那么a+c b+c不等式两边都乘(或除以)
同一个正数
6>26×5 2×5,>不变不变-2<4(-2)÷2 4÷2<.........不等式性质2:不等式两边乘(或除以)同一个正数,不等号的方向 。不变(用>或<填空)你发现了什么?>6÷5 2÷5(-2)×2 4×2,<不等号
的方向 如果a>b,c>0那么ac bc或,字母表示为:×3÷3 > > 不等式的性质2: 不等式两边都乘(或除以)
同一个负数
6>26×(-2) 2×(-2),-2<4改变改变.........>改变(用>或<填空)你发现了什么?6 ÷(-2) 2 ÷(-2)><-2÷(-4 ) 4÷(-4)-2×(-4 ) 4×(-4)<不等号
的方向不等式性质3:不等式两边乘( 或除以)同一个负数,不等号的方向 。如果a>b,c<0
那么ac bc,不等式的性质3,也可以用字母表示为:﹤﹤ 不等式的性质与等式的性质有什么相同点、不同点? 设a>b,用不等号连结下列各题中的两式。 (1)a-3 b-3
(2)2a 2b (3)-a -b 设m>n,用“>”或“<”填空:
(1)m-5 n-5(根据不等式的性质 )
(2)1/2m 1/2n (根据不等式的性质 )
(3)-3/2m -3/2n(根据不等式的性质 )
(4)2m-3 2n-3(根据不等式的性质 ) > ><>><231小试牛刀>1、2(1)如果x-5>4,那么两边都加上5,根据不等式的性质 ,可以得到 。
(2)如果 1/2 x < 3,那么两边都乘以2,
根据不等式的性质 ,可得到 。范例学习(3)如果-3x>9,那么两边都除以-3,
根据不等式的性质 ,可得到 。例1填空:x>92x < 63x <- 31回味无穷本节课你的收获是什么? 1、不等式的性质1、2、3 2、将不等式化为:x﹥a 或x﹤a的
形式
3、在数学中注意运用类比的思想 方法 作业:
选做题: P127 习题9.1
第6题
P127习题9.1:第4、5题人之所以能,
是相信能。谢谢指导!例2、利用不等式的性质解下列不等式,并把不等式的解集用数轴表示出来。学 以 致 用(1)(2)方法指导:解不等式时也可以“移项”,请你尝试用“移项”的方法解上述不等式。(1)移项要变号,(2)不等式两边除以同一个负数时,不等号方向要改变。
(1) x-7>26分析:解未知数为x的不等式,就是要使不等式逐步化为x﹥a或x﹤a的形式.
解:(1)为了使不等式x-7>26中不等号的一边变为x,根据不等式的性质1,不等式两边都加7,不等号的方向不变,得
x-7+7﹥26+7
x﹥33
这个不等式的解集在数轴上的表示如图,
锋 芒 初 试 (2) 3x<2x+1 3x-2x﹤2x+1-2x
x﹤1 解:为了使不等式3x<2x+1中不等号的一边变为x,根据 ,不等式两边都减去 ,不等号的方向 ,得这个不等式的解在数轴上的表示如图注意:解不等式时也可以“移项”,即把不等式的一边的某项变号后移到另一边,而不改变不等号的方向.言必有“据”不等式的性质12x不变
