三角形中位线
图片预览







文档简介
课件21张PPT。 福州时代中学
王清 三角形中位线2008.4.12一、教材分析
二、教法和学法分析
三、教学过程设计
四、板书设计
五、教学设计说明
六、教学评价分析一、教材分析1、教材所处的地位和作用
2、教学目标
3、教学重点与难点知识技能目标
过程与方法
情感态度价值观 二、教法和学法分析 本节课采用探究发现式教学方法,由浅入深,由简单到复杂地提出问题,鼓励学生采用观察分析,自主探索,合作交流的学习方法,让学生经历数学知识的发现、形成与应用的过程。三、教学过程设计1.折纸导入——定义引入(5分钟)
2.猜想与发现——问题提出(5分钟)
3.实验与论证——定理探究(15分钟)
4.应用与拓展——应用探究(15分钟)
5.小结与反思——知识回顾(4分钟)
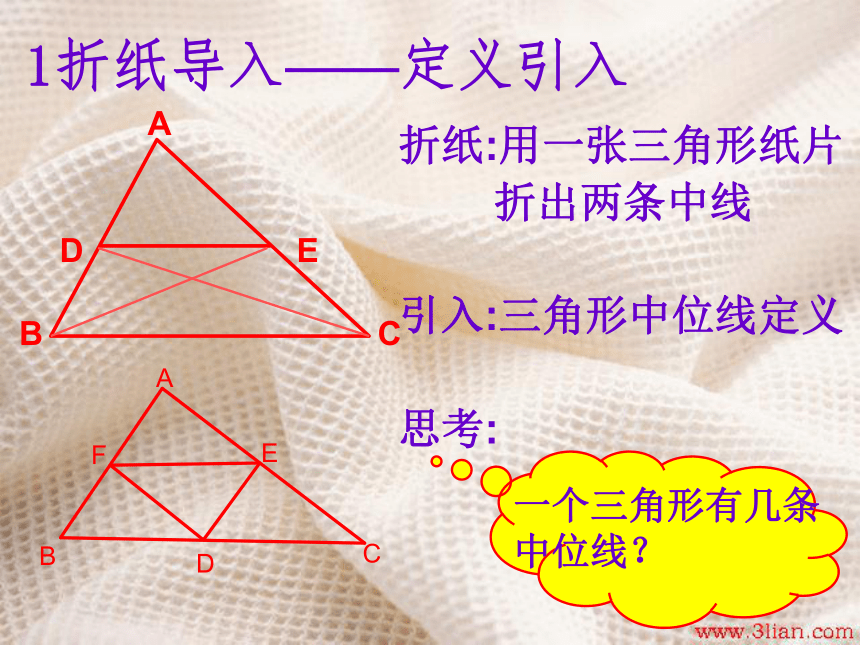
6.布置作业——继续探究(1分钟)1折纸导入——定义引入折纸:用一张三角形纸片
折出两条中线
引入:三角形中位线定义
思考:ABCDE2猜想与发现——问题提出猜想:
三角形中位线与第三边的位置及数量关系?
发现:
三角形中位线平行且等于第三边的一半。
问题:
你能用几何方法论证吗?3实验与论证——定理探究(1)利用实验活动,初步探究定理
(2)利用几何方法,进行定理推导3.实验与论证——定理探究(1)利用实验活动,
初步探究定理
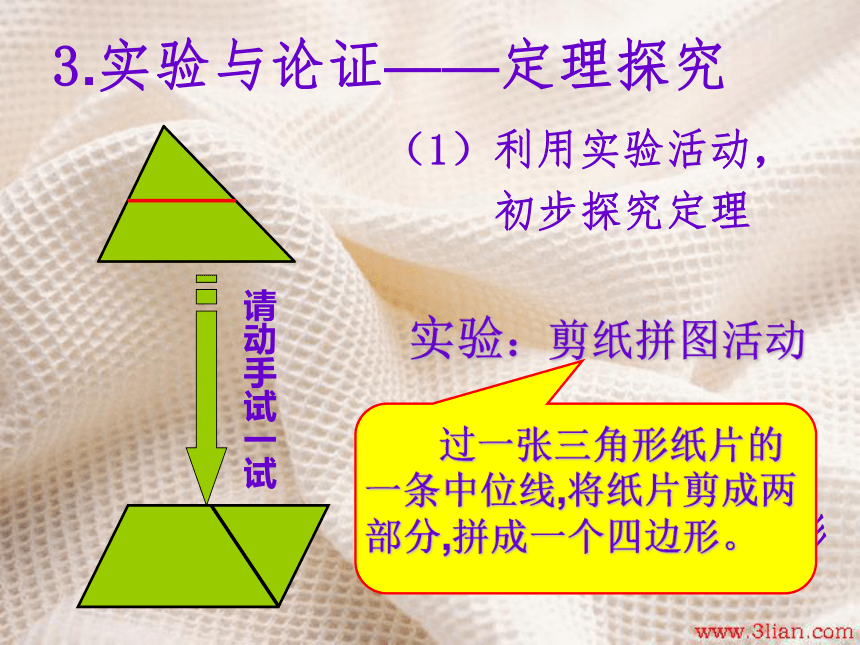
实验:剪纸拼图活动
观察:四边形形状
——平行四边形请动手试一试3.实验与论证——定理探究(1)利用实验活动,
初步探究定理
问题1:
要求观察剪痕,猜想剪痕(三角形中位线)与第三边
的位置及数量关系。
(平行四边形性质的运用) 请动手试一试3实验与论证——定理探究
(2)利用几何方法,进行定理推导
问题2:
你能用几何方法证明你的猜想吗?
——定理归纳3.实验与论证——定理探究方法1:延长DE到F点使EF=DE,
连接FC,
方法2:延长DE到F点使EF=DE,
连接FC,AF,DC,
(三角形问题“转化”为平行四边形问题 )EDAF4应用与拓展——应用探究例1(初探用途)—— (课本P99练习1改编)
如图,已知△ABC的三边分别为4cm,6cm,8cm,
则连接各边中点所成△DEF的周长为______cm。
探究1 你能发现的周长与原的周长之间
有什么关系吗?
探究2 你能发现图中有平行四边形吗?
如果有能找出几个?
探究3 你能找出图中有哪些三角形全等吗?
探究4 你能得出△DEF的面积与△ABC的面积
数量关系吗?4应用与拓展——应用探究 例2(实际应用)
如图,A﹑B两点被池塘隔开(不可到达),在A﹑B外选一点C,连接AC和BC,怎样测出A﹑B两点的实际距离?根据是什么?ABCDE(将实际问题“转化”为三角形中位线问题 )4应用与拓展——应用探究 例3(灵活应用)
如图、在四边形ABCD中,E﹑F﹑G﹑H分别是边AB﹑BC﹑CD﹑DA的中点,试问四边形EFGH是平行四边形吗?证明你的判断。(将平行四边形问题“转化”为三角形中位线问题 )5小结与反思——知识回顾收获:
1.三角形中位线定义﹑定理
2.理解和运用数学的“转化”思想解决
有关问题。
困惑?
继续探究:6布置作业——继续探究(1)巩固型作业
A.(必做题)课本P101第7题、1+1P86第3题、
1+1P87第2题、1+1P88第4题;
B.(选做题) 1+1P87第3题、1+1P88第1题。
(2)拓展型作业
Cn= ? Sn=?四、板书设计 课题:三角形中位线
定理证明 例题证明
定义: 例1:
定理: 例2:
例3:
拼图位置五、教学设计说明 根据”新课程标准”的具体目标,结合初中学生的个性特点,通过设计剪纸游戏的动手实践——直观感知——猜想、发现——几何论证,整个活动始终贯穿于三角形中位线定理的探究过程中,让学生感悟知识的
发现——生成——发展应用的过程。帮助他们在自主探索和合作交流的过程中,真正理解和掌握基本的数学知识与技能、数学思想与方法,获得广泛的数学活动经验。六、教学评价分析教师的教:“听”数学——“做”数学
“授之以鱼,不如授之以渔”学生的学:知识的理解、技能的掌握
数学“转化”思想方法的运用
数学学习态度的变化
谢谢!
王清 三角形中位线2008.4.12一、教材分析
二、教法和学法分析
三、教学过程设计
四、板书设计
五、教学设计说明
六、教学评价分析一、教材分析1、教材所处的地位和作用
2、教学目标
3、教学重点与难点知识技能目标
过程与方法
情感态度价值观 二、教法和学法分析 本节课采用探究发现式教学方法,由浅入深,由简单到复杂地提出问题,鼓励学生采用观察分析,自主探索,合作交流的学习方法,让学生经历数学知识的发现、形成与应用的过程。三、教学过程设计1.折纸导入——定义引入(5分钟)
2.猜想与发现——问题提出(5分钟)
3.实验与论证——定理探究(15分钟)
4.应用与拓展——应用探究(15分钟)
5.小结与反思——知识回顾(4分钟)
6.布置作业——继续探究(1分钟)1折纸导入——定义引入折纸:用一张三角形纸片
折出两条中线
引入:三角形中位线定义
思考:ABCDE2猜想与发现——问题提出猜想:
三角形中位线与第三边的位置及数量关系?
发现:
三角形中位线平行且等于第三边的一半。
问题:
你能用几何方法论证吗?3实验与论证——定理探究(1)利用实验活动,初步探究定理
(2)利用几何方法,进行定理推导3.实验与论证——定理探究(1)利用实验活动,
初步探究定理
实验:剪纸拼图活动
观察:四边形形状
——平行四边形请动手试一试3.实验与论证——定理探究(1)利用实验活动,
初步探究定理
问题1:
要求观察剪痕,猜想剪痕(三角形中位线)与第三边
的位置及数量关系。
(平行四边形性质的运用) 请动手试一试3实验与论证——定理探究
(2)利用几何方法,进行定理推导
问题2:
你能用几何方法证明你的猜想吗?
——定理归纳3.实验与论证——定理探究方法1:延长DE到F点使EF=DE,
连接FC,
方法2:延长DE到F点使EF=DE,
连接FC,AF,DC,
(三角形问题“转化”为平行四边形问题 )EDAF4应用与拓展——应用探究例1(初探用途)—— (课本P99练习1改编)
如图,已知△ABC的三边分别为4cm,6cm,8cm,
则连接各边中点所成△DEF的周长为______cm。
探究1 你能发现的周长与原的周长之间
有什么关系吗?
探究2 你能发现图中有平行四边形吗?
如果有能找出几个?
探究3 你能找出图中有哪些三角形全等吗?
探究4 你能得出△DEF的面积与△ABC的面积
数量关系吗?4应用与拓展——应用探究 例2(实际应用)
如图,A﹑B两点被池塘隔开(不可到达),在A﹑B外选一点C,连接AC和BC,怎样测出A﹑B两点的实际距离?根据是什么?ABCDE(将实际问题“转化”为三角形中位线问题 )4应用与拓展——应用探究 例3(灵活应用)
如图、在四边形ABCD中,E﹑F﹑G﹑H分别是边AB﹑BC﹑CD﹑DA的中点,试问四边形EFGH是平行四边形吗?证明你的判断。(将平行四边形问题“转化”为三角形中位线问题 )5小结与反思——知识回顾收获:
1.三角形中位线定义﹑定理
2.理解和运用数学的“转化”思想解决
有关问题。
困惑?
继续探究:6布置作业——继续探究(1)巩固型作业
A.(必做题)课本P101第7题、1+1P86第3题、
1+1P87第2题、1+1P88第4题;
B.(选做题) 1+1P87第3题、1+1P88第1题。
(2)拓展型作业
Cn= ? Sn=?四、板书设计 课题:三角形中位线
定理证明 例题证明
定义: 例1:
定理: 例2:
例3:
拼图位置五、教学设计说明 根据”新课程标准”的具体目标,结合初中学生的个性特点,通过设计剪纸游戏的动手实践——直观感知——猜想、发现——几何论证,整个活动始终贯穿于三角形中位线定理的探究过程中,让学生感悟知识的
发现——生成——发展应用的过程。帮助他们在自主探索和合作交流的过程中,真正理解和掌握基本的数学知识与技能、数学思想与方法,获得广泛的数学活动经验。六、教学评价分析教师的教:“听”数学——“做”数学
“授之以鱼,不如授之以渔”学生的学:知识的理解、技能的掌握
数学“转化”思想方法的运用
数学学习态度的变化
谢谢!
