3.3 相似三角形的性质和判定（2）

课件19张PPT。3.3 相似三角形的性质和判定
第2课时 两角对应相等的三角形是相似三角形 湖南省新邵县酿溪中学王军旗学习目标 1、通过画图知道有两个角对应相等的三角形相似。
2、理解相似三角形的判定定理（二），并能用它
判定三角形相似。
3、理解相似三角形的两条性质。1、全等三角形有哪些判定方法？ SSS,SAS,AAS,ASA ,HL复习提问2、相似三角形的判定方法你学了哪两条？（1）按定义判三边对应成比例，三个角对应相等。
（2）只要判定三边对应成比例，就可以得到两个
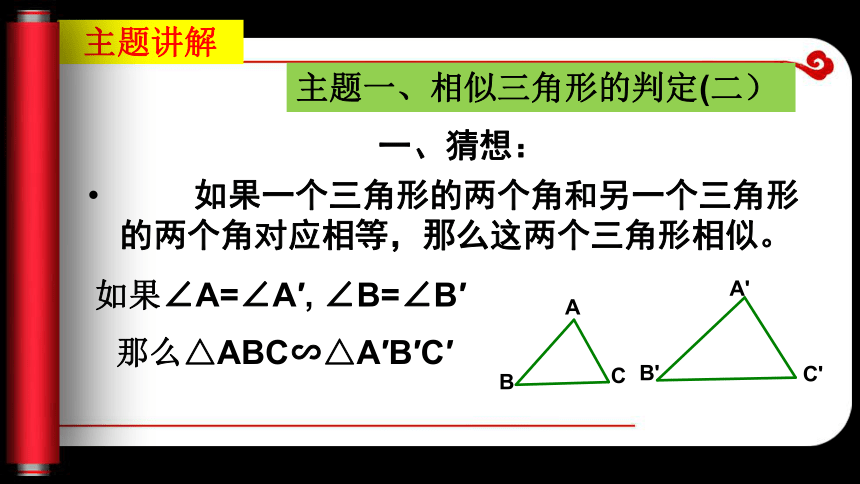
三角形相似。 判定三角形相似，按定义需要判定三边对应成比例，三个角对应相等，能否像判定三角形全等一样减少一些条件呢？三边对应成比例的两个三角形相似和全等三角形判定方法中的哪一条类似？新课引言类似SSS 你能由AAS,ASA猜想相似三角形还有什么判定方法吗？主题讲解 如果一个三角形的两个角和另一个三角形的两个角对应相等，那么这两个三角形相似。主题一、相似三角形的判定(二）一、猜想：如果∠A=∠A′, ∠B=∠B′那么△ABC∽△A′B′C′方法：
①每个同学画一个三角形ABC，使∠A=30o,∠B=45o,再量一量三边的长度。
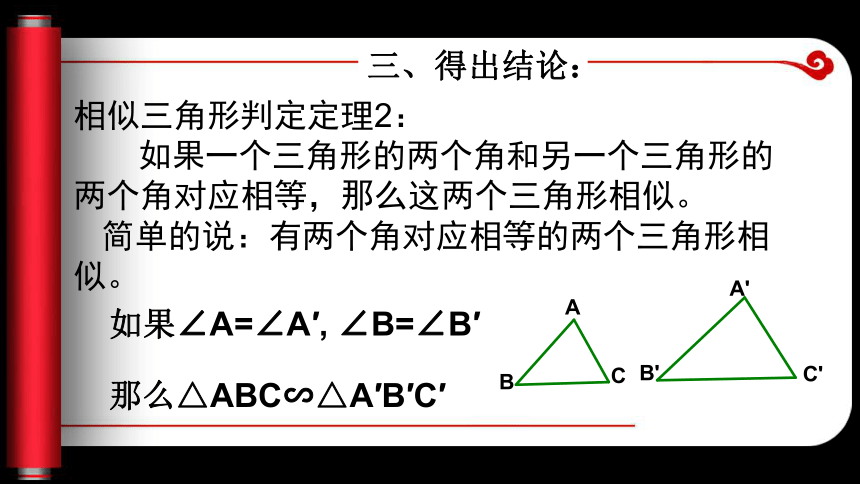
②与同桌同学的对比，看看你们画的两个三角形三边是否对应成比例。二、验证几何画板演示相似三角形判定定理2： 如果一个三角形的两个角和另一个三角形的两个角对应相等，那么这两个三角形相似。 简单的说：有两个角对应相等的两个三角形相似。三、得出结论：如果∠A=∠A′, ∠B=∠B′那么△ABC∽△A′B′C′例1如图△A′B′C′∽△ABC，相似比为k，分别作BC, B′C′上的高，AD，A′D′求证：A′D′:AD=k分析：由于相似比是对应边的比，所以A′B′:AB=k,因此关键是判定:
A′D′:AD=A′B′:AB, 或A′D′:AD=A′C′:AC所以需要判断△ A′B′D′ ∽△ ABD或△A′D′C′ ∽ △ADC
主题二、相似三角形的性质证明：
∵△A′B′C′∽△ABC∴∠B′=∠B,
∵∠A′D′B′=∠ADB =90o
∴△A′D′B′∽△ABD,
∴A′D′:AD=A′B′:AB=k.
思考：由上面例题你能得出什么结论？相似三角形对应高的比等于相似比。
“对应”的含义，即甲三角形的高比乙三角形的高等于甲三角形的边比乙三角形的对应边。注意！例2．已知△A′B′C′∽△ABC，相似比为k，
那么它们周长的比等于____,面积的比等于_____.k例2．已知△A′B′C′C∽△ABC，相似比为k，
那么它们周长的比等于____,面积的比等于_____.思考：由此你得到了什么结论？ 相似三角形周长的比等于相似比，面积的比等于相似比的平方。 变式练习： 1、已知△ABC∽△A′B′C′,它们的周长分别为60cm,72cm,AB=15cm,B′C′=24cm,
则BC=__,AC=___,A′B′=__,A′C′=___,主题三、相似三角形判定定理2的应用例3已知在△ABC与△DEF中，∠A=48o,∠B=82o,∠D=48o,∠F=50o
求证：△ABC∽△DEF
解：在△DEF中，∠E=180o-∠D-∠F=180o-48o-50o=82o
解：在△DEF中，
∠E=180o-∠D-∠F=180o-48o-50o=82o∵∠B=∠E=82o, ∠A=∠D =48o,
∴△ABC∽△DEF例4．已知在△ABC中，DE∥BC,求证：△ADE∽△ABC证明：∵DE∥BC,
∴∠ADE=∠B,
∵∠A=∠A,
∴△ADE∽△ABC
?
变式练习：已知△ABC中，D、E分别是AC，AB上的点，且∠AED=∠C，
求证：△ADE∽△ABC证明：∵ ∠AED=∠C， ∠A=∠A，∴△ADE∽△ABC1、判定三角形相似学了两种方法（1）三边对应相等的两个三角形相似；（2）两个角对应相等的两个三角形相似。2、相似三角形除对应边成比例，对应角相等外还有对应高的比等于相似比，周长的比等于相似比，面积的比等于相似的平方。小结作业：P76 练习1---5（做到书上）P 79— 80A 3、4B 2、3.