3.3 相似三角形的性质和判定3

课件19张PPT。3.3 相似三角形的性质和判定
第3课时 两边对应成比例且夹角
相等的两个三角形是相似三角形湖南省新邵县酿溪中学王军旗学习目标 1、通过画图探究相似三角形的判定定理3.
2、理解相似三角形的判定定理3，并能用 它判定三角形相似。复习提问相似三角形除定义外还学过哪些判定方法？（1）三边对应成比例的两个三角形相似。
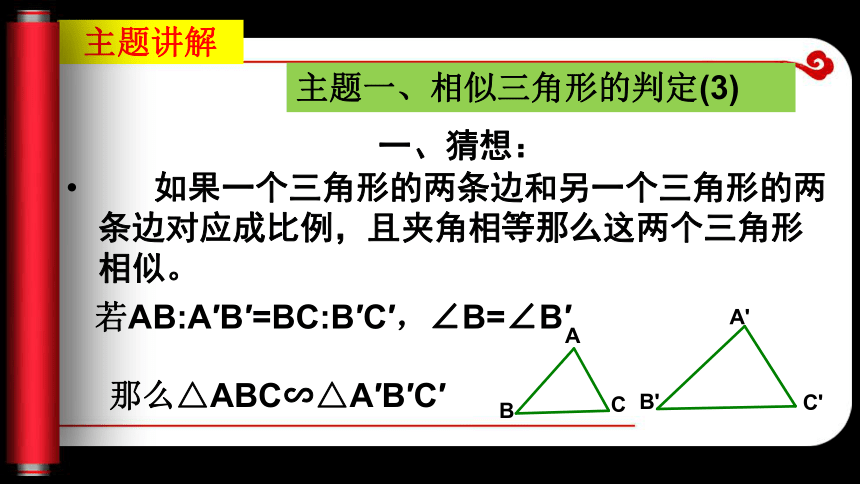
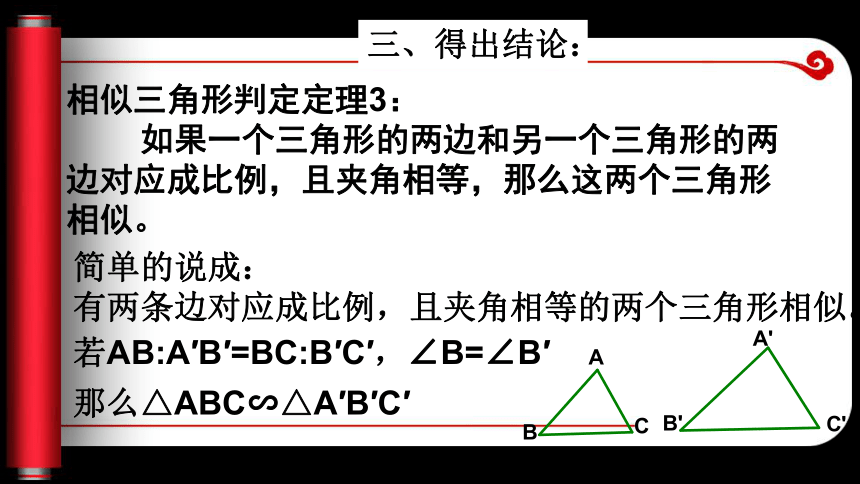
（2）两个角对应相等的两个三角形相似。抽签器 三边对应成比例的两个三个角相似类似于全等三角形的判定方法SSS，有两个角对应相等的三角形相似类似于全等三角形的AAS、ASA,新课引言 你能由SAS, 猜想相似三角形还有什么判定方法吗？主题讲解 如果一个三角形的两条边和另一个三角形的两条边对应成比例，且夹角相等那么这两个三角形相似。主题一、相似三角形的判定(3)一、猜想：若AB:A′B′=BC:B′C′，∠B=∠B′那么△ABC∽△A′B′C′方法：.画两个三角形△ABC，△A ′B ′C ′ ,使 AB:A ′ B ′ =BC:B ′ C ′ = 2，且使∠B=∠B ′ ,然后测量一对对应角看它是否相等，或第三条边的比是否为2.就可以验证这两个三角形是否相似了。二、验证几何画板演示 相似三角形判定定理3： 如果一个三角形的两边和另一个三角形的两边对应成比例，且夹角相等，那么这两个三角形相似。 三、得出结论：若AB:A′B′=BC:B′C′，∠B=∠B′那么△ABC∽△A′B′C′简单的说成：
有两条边对应成比例，且夹角相等的两个三角形相似。思考：1、能否再减少夹角相等的条件。
即：有两边对应成比例的两个三角形相似几何画板演示只有两条边对应成比例的两个三角形不一定相似。注意！思考2、夹角相等能否改为一条边的对角对应相等呢？即：有两条边对应成比例，且其中一条边的对角对应相等。那么这两个三角形相似。 有两条边对应成比例，且其中一条边的对角对应相等的两个三角形不一定相似注意！几何画板演示主题二、相似三角形的判定定理(3)的应用例1已知△ABC与△DEF中，∠C=∠F=70 o,AC=3.5cm,BC=2.5cm,DF=2.1cm,EF=1.5cm,求证：△DEF∽△ABC【分析】题目没有画图，我们要根据题意画出简图，已知一对对应角相等，且知道四条边的长，所以考虑观察夹这一对对应角的边是否成比例。证明：设A′C′=b，A′B′=c,则AC=2b,AB=2c.
想一想：
1、除了用两边对应成比例，且夹角相等证明这两个三角形相似外，还可以用什么方法证明这两个三角形相似？2、把 改成任意正数k，Rt △A’B’C’∽△ABC吗？主题三、相似三角形性质和判定的综合应用解：在△DEF中，∠E=180o-∠D-∠F=180o-48o-50o=82o
变式练习：1、 Rt△ABC与、 Rt△A’B’C’中∠C=∠C’,AC=3cm,BC=2cm,
A ′ C′=4.2cm,B’C’=2.8cm
求证： △A’B’C’ ∽ △ABC∵∠C=∠C’ ，∴ △A’B’C’ ∽ △ABC2、如图△ABC中，CD⊥AB于D，CD2=AD·BD.
求证：△CDA∽△BDC
?
证明：∵CD⊥AB, ∴∠CDA=∠BDC=90o∵ CD2=AD·BD, ∴CD:AD=BD:CD∴ △CDA∽△BDA(两边对应成比例且夹角相等的三角形相似。 小结判定三角形相似学了三种方法（1）三边对应相等的两个三角形相似；（2）两个角对应相等的两个三角形相似
（3）两边对应成比例且夹角相等的两个三角形全等。作业：P79--81A 4、5、6、7、8（第7题写到书上）