(北师大版必修5)数学:《2.3解三角形的实际应举例-三角函数模型的应用》 课件
文档属性
| 名称 | (北师大版必修5)数学:《2.3解三角形的实际应举例-三角函数模型的应用》 课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 388.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-28 00:00:00 | ||
图片预览




文档简介
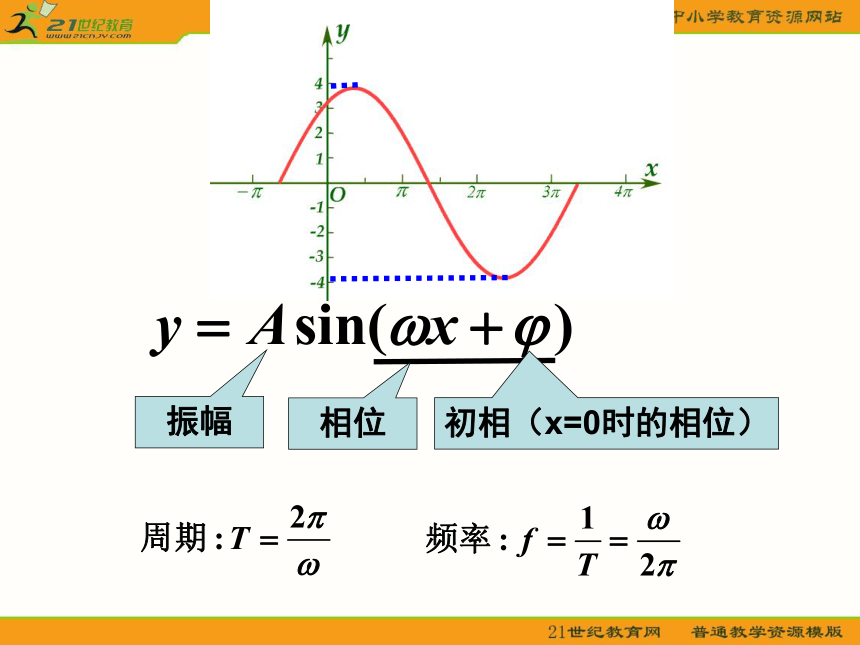
课件16张PPT。三角函数模型的简单应用 振幅初相(x=0时的相位)相位例1. 如图:点O为作简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向,若已知振幅为3cm,周期为3s,且物体向右运动到距离平衡位置最远时开始计时。
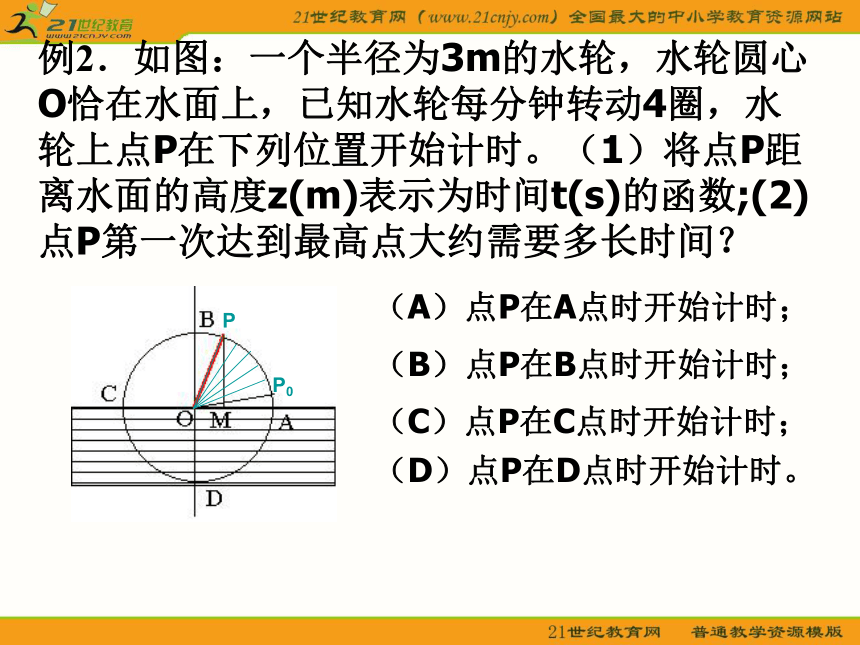
(1)求物体对平衡位置的位移x(cm)和时间t(s)之间的函数关系;(2)求物体在t=5s时的位置。 例2.如图:一个半径为3m的水轮,水轮圆心O恰在水面上,已知水轮每分钟转动4圈,水轮上点P在下列位置开始计时。(1)将点P距离水面的高度z(m)表示为时间t(s)的函数;(2)点P第一次达到最高点大约需要多长时间? P0
(A)点P在A点时开始计时; (B)点P在B点时开始计时; (C)点P在C点时开始计时; (D)点P在D点时开始计时。 P
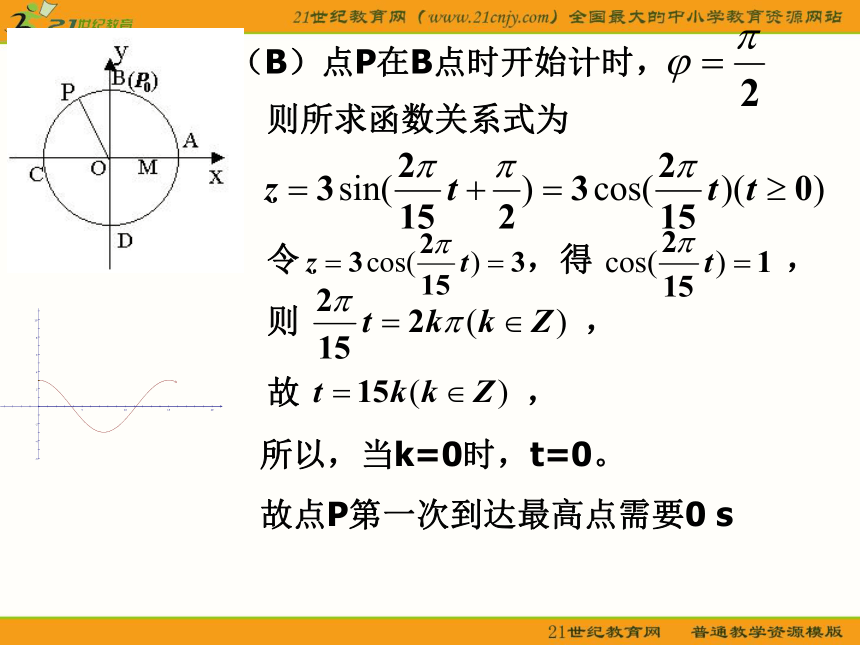
解:不妨设水轮沿逆时针方向旋转,如图建立平面直角坐标系。 (A)点P在A点时开始计时, 则所求函数关系式为(B)点P在B点时开始计时, 所以,当k=0时,t=0。
故点P第一次到达最高点需要0 s则所求函数关系式为(C)点P在C点时开始计时, 则所求函数关系式为 (D)点P在D点时开始计时, 则所求函数关系式为(A)点P在A点时开始计时; (B)点P在B点时开始计时; (C)点P在C点时开始计时; (D)点P在D点时开始计时。 变题:将圆心O上移2米,其余不变,试求解。圣米切尔山涨潮落潮 潮汐对轮船进出港口产生什么影响? 某港口在某季节每天的时间与水深关系表:例3:A=2.5,h=5,T=12 ;所以,这个港口的水深与时间的关系可以近似描述为:由上述关系式易得港口在整点时水深的近似值:小结:
(1)求物体对平衡位置的位移x(cm)和时间t(s)之间的函数关系;(2)求物体在t=5s时的位置。 例2.如图:一个半径为3m的水轮,水轮圆心O恰在水面上,已知水轮每分钟转动4圈,水轮上点P在下列位置开始计时。(1)将点P距离水面的高度z(m)表示为时间t(s)的函数;(2)点P第一次达到最高点大约需要多长时间? P0
(A)点P在A点时开始计时; (B)点P在B点时开始计时; (C)点P在C点时开始计时; (D)点P在D点时开始计时。 P
解:不妨设水轮沿逆时针方向旋转,如图建立平面直角坐标系。 (A)点P在A点时开始计时, 则所求函数关系式为(B)点P在B点时开始计时, 所以,当k=0时,t=0。
故点P第一次到达最高点需要0 s则所求函数关系式为(C)点P在C点时开始计时, 则所求函数关系式为 (D)点P在D点时开始计时, 则所求函数关系式为(A)点P在A点时开始计时; (B)点P在B点时开始计时; (C)点P在C点时开始计时; (D)点P在D点时开始计时。 变题:将圆心O上移2米,其余不变,试求解。圣米切尔山涨潮落潮 潮汐对轮船进出港口产生什么影响? 某港口在某季节每天的时间与水深关系表:例3:A=2.5,h=5,T=12 ;所以,这个港口的水深与时间的关系可以近似描述为:由上述关系式易得港口在整点时水深的近似值:小结:
