(北师大版必修5)数学:《第一章 数列》复习课件
文档属性
| 名称 | (北师大版必修5)数学:《第一章 数列》复习课件 |  | |
| 格式 | rar | ||
| 文件大小 | 266.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-28 20:12:00 | ||
图片预览






文档简介
课件16张PPT。数学必修⑤《数列》
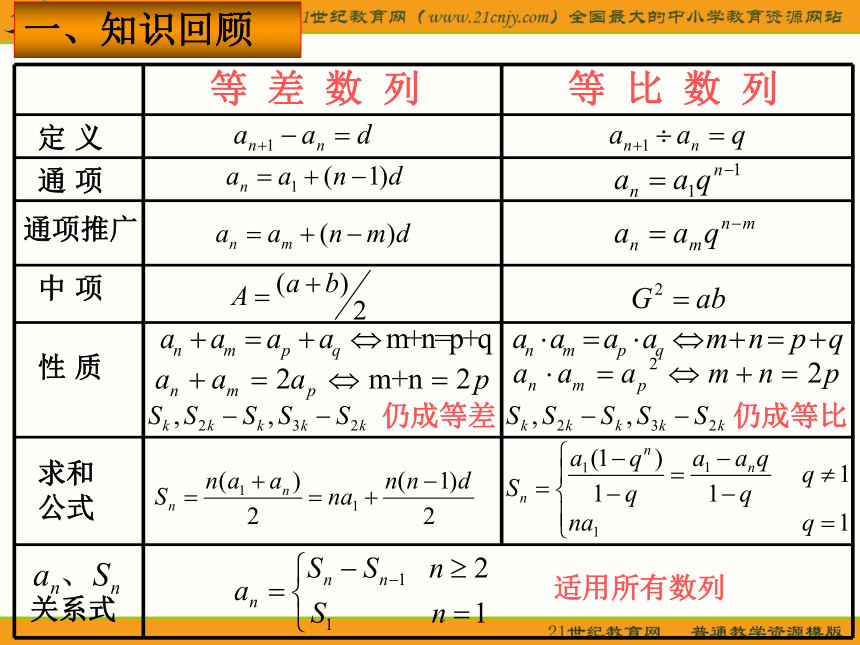
单元总结复习 数列是高中代数的重要内容,又是学习高等数学的基础,所以在高考中占有重要的地位,是高考数学的主要考察内容之一,试题难度分布幅度大,既有容易的基本题和难度适中的小综合题,也有综合性较强对能力要求较高的难题。大多数是一道选择或填空题,一道解答题。解答题多为中等以上难度的试题,突出考查考生的思维能力,解决问题的能力,试题经常是综合题,把数列知识和指数函数、对数函数和不等式的知识综合起来,探索性问题是高考的热点,常在数列解答题中出现。应用问题有时也要用到数列的知识。试题特点 一、知识回顾仍成等差仍成等比等 差 数 列等 比 数 列定 义通 项通项推广中 项性 质求和公式关系式适用所有数列Ⅰ 、等差、等比数列的设法及应用1.三个数成等差数列可设为 或者 ,2. 三个数成等比数列,则这三个数可设为 ,也可以设为 例1(1). 已知三个数成等差数列,其和为15,其平方和为83,求此三个数.析:设这三个数为则∴所求三个数分别为3,5,7解得x=5,d=或7,5,3.±2.二、知识应用根据具体问题的不同特点而选择不同设法。例1(2):互不相等的三个数之积为 ,这三个数适当排列后可成为等比数列也可排成等差数列,求这三数排成的等差数列.设这三个数为, 则即:即:与已知三数不等矛盾即:三个数为或即:三个数为或综上:这三数排成的等差数列为:Ⅱ 、运用等差、等比数列的性质例2(1)已知等差数列 满足 ,则 ( )(3)已知在等差数列{an}的前n项中,前四项之和为21,后四项之和为67,前n项之和为286,试求数列的项数n.析:C (2)已知等差数列 前 项和为30,前 项和为100,则前 项和为 ( )C考题剖析 已知{an}为等差数列, a2+a8=12,,则a5等于( )
(A)4 (B)5 (C)6 (D)7 解:由已知,由等差数列的性质,有a2+a8=2a5,
所以,a5=6,选(C)。
[点评]本题直接利用等差数列的性质,由等差中项
可得,属容易题。例3.等差数列{an}中,a1<0,S9=S12,该数列前多少项的和最小?分析:如果等差数列{an}由负数递增到正数,或者由正数递减到负数,那么前n项和Sn有如下性质:1.当a1<0,d>0时,2.当a1>0,d<0时,思路1:寻求通项∴n取10或11时Sn取最小值即:易知由于Ⅲ、等差数列的最值问题例3.等差数列{an}中,a1<0,S9=S12,该数列前多少项的和最小?分析:等差数列{an}的通项an是关于n的一次式,前项和Sn是关于n的二次式(缺常数项).求等差数列的前n项和 Sn的最大最小值可用解决二次函数的最值问题的方法.思路2:从函数的角度来分析数列问题.设等差数列{an}的公差为d,则由题意得:∵a1<0, ∴ d>0,∵d>0, ∴Sn有最小值.又∵n∈N*, ∴n=10或n=11时,Sn取最小值即:例3.等差数列{an}中,a1<0,S9=S12,该数列前多少项和最小?分析:数列的图象是一群孤立的点,数列前 n项和Sn 的图象也是一群孤立的点.此题等差数列前n项和Sn的图象是在抛物线上一群孤立的点.求Sn的最大最小值即要求距离对称轴最近的正整数n.因为S9=S12,又S1=a1<0,所以Sn 的图象所在的抛物线的
对称轴为直线n=(9+12) ÷2=10.5,所以Sn有最小值∴数列{an}的前10项或前11项和最小nSnon=10.5类比:二次函数f(x),若 f(9)=f(12),则函数f(x)图象的对称轴为直线x=(9+12) ÷2=10.5若f(x+2)=f(2-x),则函数f(x)图象的对称轴为直线x=2思路3:函数图像、数形结合令故开口向上过原点抛物线 设等差数列 {an} 的公差为d,等比数列 {bn} 的公比为 ,则由题意得解析:通项特征:由等差数列通项与等比数列通项相乘而得求和方法:错位相减法——错项法 Ⅳ 、等差、等比数列的综合应用 解析: 两式相减: 错位相减法1.观察数列:30,37,32,35,34,33,36,( ),38的特点,在括号内适当的一个数是______2.在等差数列中,a4+a6=3,则a5(a3+2a5+a7)=_____3. 在等差数列{an}中,若a4+a6+a8+a10+a12=120,则
2a10-a12的值为 ( )
A.20 B.22 C.24 D.28319C4.若{an}是等比数列,且an>0,a2a4+2a3a5+a4a6=25,那
么a3+a5的值等于 ( )A.5 B.1 C.15 D.10A三、基础练习5.等差数列{an}中,已知前4项和是1,前8项和是4,则
a17+a18+a19+a20的值等于 ( )A.7 B.8 C.9 D.10C 7.首项为-24的等差数列从第10项开始为正数,求公差为d的取值范围8.在数列{an}中,a1=3,an+1=an+3n(n≥1),求此数列的通项公式三、基础练习6.三数成等比数列,若将第三数减去32,则成等差数列,若再将等差数列的第二个数减去4,又成等比数列,原来三个是:____________________.
考题剖析 例5、数列{an}满足
(Ⅰ)当a2=-1时,求λ及a3的值;
(Ⅱ)数列{an}是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由; 解:(Ⅰ)由于 且a1=1,
所以当a2=-1时,得, 故
从而
(Ⅱ)数列{an}不可能为等差数列.证明如下:
由a1=1, 得
若存在λ ,使{an}为等差数列,则a3-a2=a2-a1,即
解得λ =3.
于是
这与{an}为等差数列矛盾,所以,对任意λ ,{an}都不可能是等差数列.
[点评]证明一个数列是等差数列,须证明这个数列的第n项与第n-1项的差是常数。
单元总结复习 数列是高中代数的重要内容,又是学习高等数学的基础,所以在高考中占有重要的地位,是高考数学的主要考察内容之一,试题难度分布幅度大,既有容易的基本题和难度适中的小综合题,也有综合性较强对能力要求较高的难题。大多数是一道选择或填空题,一道解答题。解答题多为中等以上难度的试题,突出考查考生的思维能力,解决问题的能力,试题经常是综合题,把数列知识和指数函数、对数函数和不等式的知识综合起来,探索性问题是高考的热点,常在数列解答题中出现。应用问题有时也要用到数列的知识。试题特点 一、知识回顾仍成等差仍成等比等 差 数 列等 比 数 列定 义通 项通项推广中 项性 质求和公式关系式适用所有数列Ⅰ 、等差、等比数列的设法及应用1.三个数成等差数列可设为 或者 ,2. 三个数成等比数列,则这三个数可设为 ,也可以设为 例1(1). 已知三个数成等差数列,其和为15,其平方和为83,求此三个数.析:设这三个数为则∴所求三个数分别为3,5,7解得x=5,d=或7,5,3.±2.二、知识应用根据具体问题的不同特点而选择不同设法。例1(2):互不相等的三个数之积为 ,这三个数适当排列后可成为等比数列也可排成等差数列,求这三数排成的等差数列.设这三个数为, 则即:即:与已知三数不等矛盾即:三个数为或即:三个数为或综上:这三数排成的等差数列为:Ⅱ 、运用等差、等比数列的性质例2(1)已知等差数列 满足 ,则 ( )(3)已知在等差数列{an}的前n项中,前四项之和为21,后四项之和为67,前n项之和为286,试求数列的项数n.析:C (2)已知等差数列 前 项和为30,前 项和为100,则前 项和为 ( )C考题剖析 已知{an}为等差数列, a2+a8=12,,则a5等于( )
(A)4 (B)5 (C)6 (D)7 解:由已知,由等差数列的性质,有a2+a8=2a5,
所以,a5=6,选(C)。
[点评]本题直接利用等差数列的性质,由等差中项
可得,属容易题。例3.等差数列{an}中,a1<0,S9=S12,该数列前多少项的和最小?分析:如果等差数列{an}由负数递增到正数,或者由正数递减到负数,那么前n项和Sn有如下性质:1.当a1<0,d>0时,2.当a1>0,d<0时,思路1:寻求通项∴n取10或11时Sn取最小值即:易知由于Ⅲ、等差数列的最值问题例3.等差数列{an}中,a1<0,S9=S12,该数列前多少项的和最小?分析:等差数列{an}的通项an是关于n的一次式,前项和Sn是关于n的二次式(缺常数项).求等差数列的前n项和 Sn的最大最小值可用解决二次函数的最值问题的方法.思路2:从函数的角度来分析数列问题.设等差数列{an}的公差为d,则由题意得:∵a1<0, ∴ d>0,∵d>0, ∴Sn有最小值.又∵n∈N*, ∴n=10或n=11时,Sn取最小值即:例3.等差数列{an}中,a1<0,S9=S12,该数列前多少项和最小?分析:数列的图象是一群孤立的点,数列前 n项和Sn 的图象也是一群孤立的点.此题等差数列前n项和Sn的图象是在抛物线上一群孤立的点.求Sn的最大最小值即要求距离对称轴最近的正整数n.因为S9=S12,又S1=a1<0,所以Sn 的图象所在的抛物线的
对称轴为直线n=(9+12) ÷2=10.5,所以Sn有最小值∴数列{an}的前10项或前11项和最小nSnon=10.5类比:二次函数f(x),若 f(9)=f(12),则函数f(x)图象的对称轴为直线x=(9+12) ÷2=10.5若f(x+2)=f(2-x),则函数f(x)图象的对称轴为直线x=2思路3:函数图像、数形结合令故开口向上过原点抛物线 设等差数列 {an} 的公差为d,等比数列 {bn} 的公比为 ,则由题意得解析:通项特征:由等差数列通项与等比数列通项相乘而得求和方法:错位相减法——错项法 Ⅳ 、等差、等比数列的综合应用 解析: 两式相减: 错位相减法1.观察数列:30,37,32,35,34,33,36,( ),38的特点,在括号内适当的一个数是______2.在等差数列中,a4+a6=3,则a5(a3+2a5+a7)=_____3. 在等差数列{an}中,若a4+a6+a8+a10+a12=120,则
2a10-a12的值为 ( )
A.20 B.22 C.24 D.28319C4.若{an}是等比数列,且an>0,a2a4+2a3a5+a4a6=25,那
么a3+a5的值等于 ( )A.5 B.1 C.15 D.10A三、基础练习5.等差数列{an}中,已知前4项和是1,前8项和是4,则
a17+a18+a19+a20的值等于 ( )A.7 B.8 C.9 D.10C 7.首项为-24的等差数列从第10项开始为正数,求公差为d的取值范围8.在数列{an}中,a1=3,an+1=an+3n(n≥1),求此数列的通项公式三、基础练习6.三数成等比数列,若将第三数减去32,则成等差数列,若再将等差数列的第二个数减去4,又成等比数列,原来三个是:____________________.
考题剖析 例5、数列{an}满足
(Ⅰ)当a2=-1时,求λ及a3的值;
(Ⅱ)数列{an}是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由; 解:(Ⅰ)由于 且a1=1,
所以当a2=-1时,得, 故
从而
(Ⅱ)数列{an}不可能为等差数列.证明如下:
由a1=1, 得
若存在λ ,使{an}为等差数列,则a3-a2=a2-a1,即
解得λ =3.
于是
这与{an}为等差数列矛盾,所以,对任意λ ,{an}都不可能是等差数列.
[点评]证明一个数列是等差数列,须证明这个数列的第n项与第n-1项的差是常数。
