(北师大版必修5)数学 第二章 第2-3节 三角形中的几何计算;解三角形的实际应用举例(文)知识精讲
文档属性
| 名称 | (北师大版必修5)数学 第二章 第2-3节 三角形中的几何计算;解三角形的实际应用举例(文)知识精讲 |

|
|
| 格式 | rar | ||
| 文件大小 | 178.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-28 20:12:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第二章 第2-3节 三角形中的几何计算;解三角形的实际应用举例(文)北师大版必修5
【本讲教育信息】
一、教学内容:
三角形中的几何计算及实际应用举例
二、教学目标
(1)体会用正弦定理、余弦定理处理三角形中的计算问题。
(2)能灵活的运用正弦定理、余弦定理解决测量、航海、台风预报等有关的实际问题,体会建立三角函数模型的思想。
(3)结合正弦定理、余弦定理等体会用方程的数学思想、分论讨论的数学思想等解决实际问题。
三、知识要点分析:
1. 三角形中的几何计算的有关知识点(三角形中的边和角的关系:)
(i)大角对大边:
(ii)正弦定理:,(R是三角形外接圆的半径)
(iii)余弦定理:
(iv)三角形的面积
S△ABC
2. 解决实际问题的有关知识点
(1)仰角与俯角:在视线与水平线所成的角中,视线在水平线上方的角叫仰角,视线在水平线下方的角叫俯角。
(2)方位角:指从正北方向顺时针转到目标方向线的夹角叫方位角。
(3)解决实际问题的步骤。
(i)理解题意分清已知与未知。(ii)画图建模利用正、余弦定理等知识点求解。(iii)作答。
3. 掌握三角形内角诱导公式及相关的结论,(i)tanA+tanB+tanC=tanAtanBtanC
(ii)
(iii)
【典型例题】
考点一:三角形中的几何计算
例1. 设D是直角三角形ABC的斜边BC上的一点,AB=AD,。
(1)求证:,(2)若求的值。
思路分析:(1)由已知找出与的关系,即,即可证明。(2)由正弦定理得到关于的方程即可。
解:(1)由AB=AD
.
①
(2)由正弦定理得:
将此式代入①得:
②
将②整理得:
又
故。即所求的角是
例2. 设P是正方形ABCD内一点,P到A、B、C的距离分别是1,2,3,求正方形ABCD的边长
思路分析:设正方形的边长为x,根据角ABP与角CBP互余,可知其余弦的平方和是1,建立关于x的方程,再求解。21世纪教育网
解:设边长是x,(1在三角形ABP中:由余弦定理得:,
同理在△CBP中: ,90°得:
即有: (*)
解*得所求的边长为。
说明:使用正弦定理或余弦定理或相关的知识点解决几何问题,首先要在已知的图形中构造三角形(已有三角形,不需构造),能构造特殊三角形的尽可能地构造特殊的三角形。
考点二:研究几何计算问题中的最值问题。
如图所示,点P在直径AB=1的半圆上移动,过点P作半圆的切线PT,使PT=1,则如何确定P点的位置?才能使得四边形ABTP的面积最大?
思路分析:由已知得P点的变化引起角PAB的变化,故可把四边形ABTP的面积表示成关于角PAB的函数,然后求函数的最值。
解:连接BP,设∠PAB=α,由AB为直径得∠APB=90°,即△APB是直角三角形,
由AB=PT=1得:。又PT是圆的切线,故,∠BPT=∠PAB=α
例4. 在等边三角形ABC中,AB=a,O为中心,过O的直线交AB于M,交AC于N,
求的最大值。
思路分析:由于M、N的变化导致角MOA的变化,然后利用正弦定理,把式子表示成角MOA的函数,再求最大值。
解:由已知∠MAO=∠NAO=30°,设∠MOA=θ,则
故当时,即时,取得最大值是。
【说明】在三角形几何计算中解决最值问题的关键是引入变量。
考点三:利用正弦定理、余弦定理解决实际问题
例5. (1)(航海问题)已知一测高仪表失灵的飞机在高空以300km/h的速度按水平方向向东飞行,飞机的航线和山顶C在同一铅直的平面内,若在A处的飞行员利用测角仪器测得先看到海拔高度为4000m的山顶C的俯角为15°,经120秒后在B点又看到山顶C的俯角是60°,求飞机现在的海拔高度。
思路分析:先根据已知条件画出图形,找出两个俯角,再根据正弦定理求出BC,在直角三角形BCD中求出CD,CD加上山的高度即是飞机现在的海拔高度。
解:根据已知画出图形(如图)∠BAC=15°,∠DBC=60°,故∠BCA=45°
又AB=300×=10(km),则在△ABC中由正弦定理得:
在直角△BDC中:CD=BCsin60°=
故飞机飞行的海拔高度是3170+4000=7170(米)
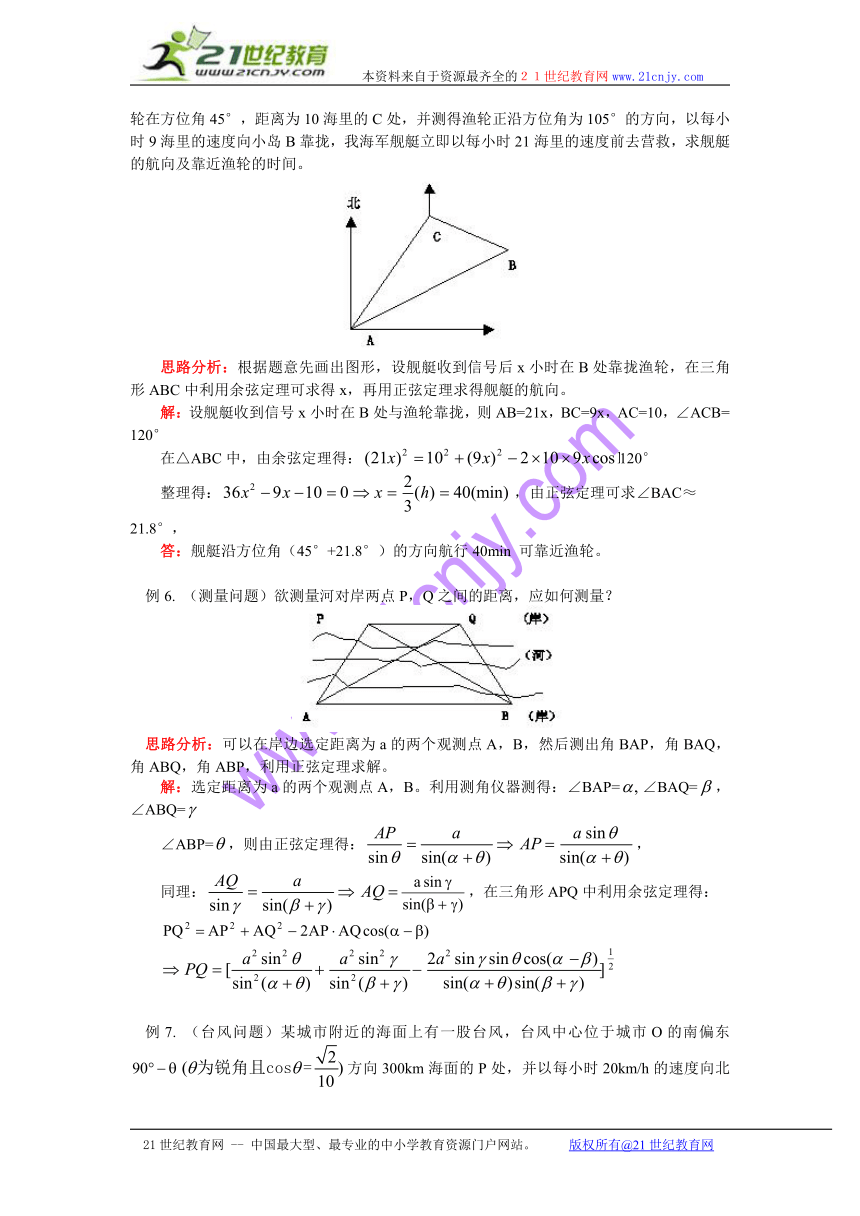
(2)某渔轮在航行中不幸遇险,发出呼救信号,我海军舰艇在A处获悉后,测出该渔轮在方位角45°,距离为10海里的C处,并测得渔轮正沿方位角为105°的方向,以每小时9海里的速度向小岛B靠拢,我海军舰艇立即以每小时21海里的速度前去营救,求舰艇的航向及靠近渔轮的时间。
思路分析:根据题意先画出图形,设舰艇收到信号后x小时在B处靠拢渔轮,在三角形ABC中利用余弦定理可求得x,再用正弦定理求得舰艇的航向。
解:设舰艇收到信号x小时在B处与渔轮靠拢,则AB=21x,BC=9x,AC=10,∠ACB=
120°
在△ABC中,由余弦定理得:120°
整理得:,由正弦定理可求∠BAC≈
21.8°,
答:舰艇沿方位角(45°+21.8°)的方向航行40min 可靠近渔轮。
例6. (测量问题)欲测量河对岸两点P,Q之间的距离,应如何测量?
思路分析:可以在岸边选定距离为a的两个观测点A,B,然后测出角BAP,角BAQ,角ABQ,角ABP,利用正弦定理求解。
解:选定距离为a的两个观测点A,B。利用测角仪器测得:∠BAP=∠BAQ=,∠ABQ=
∠ABP=,则由正弦定理得:,
同理:,在三角形APQ中利用余弦定理得:
例7. (台风问题)某城市附近的海面上有一股台风,台风中心位于城市O的南偏东方向300km海面的P处,并以每小时20km/h的速度向北偏西45°的方向移动,台风侵袭的范围为圆形区域,当时半径是60km,并以10km/h的速度不断增大,问几小时后该城市受到台风的侵袭?21世纪教育网
思路分析:设经过x小时该城市恰好受到台风的侵袭,假设台风中心由P移到Q处(如图),此时台风的侵袭半径是OQ=60+10x,在三角形OPQ中,OP=300,PQ=20x,由余弦定理建立关于x的方程求x。
解:设x小时后该城市恰好受到台风的侵袭,此时台风中心由P处移到Q处,台风的侵袭半径是(60+10x)km,城市O恰好受到台风侵袭的条件是OQ=60+10x
在三角形OPQ中:OP=300,PQ=20x,∠OPQ=-45°,cos∠OPQ=cos(-45°)
=,
由余弦定理得:
故方程无解,即该城市不会受到台风的影响。
【本讲涉及的数学思想、方法】
本讲主要讲述了利用正弦定理、余弦定理及其相关的知识解决三角形中的几何计算及实际问题,在此过程中,体现了方程的数学思想(如例1、例2)、函数的数学思想(如求最值问题)、等价转化的数学思想等在解题中的应用。
预习导学案
(不等关系及一元二次不等式的解法)
一:预习前知
1. 在初中你学过不等式有哪些性质?
2. 解一元一次不等式的步骤有哪些?
3. 解关于x的不等式:ax>b (a,b是实数)
4. 二次函数的关系是什么?
二:预习导学
探究、反思
探究反思的任务:不等关系、一元二次不等式的解法
1、举例说明在现实生活中的不等关系。
【反思】比较两个实数大小的方法有哪些?(作差比较,作商比较)
a-b>0
2、不等式的性质有哪些?
传递性_________,(2)加法单调性_________,(3)乘法单调性_________。(4)同向不等式相加______________(5)两边都是正数的同向不等式相乘_____________。
【反思】由上面的性质你能证明:a>b>0,吗?
3、一元二次不等式的定义:_____________________________________________。
4、一元二次不等式的解法的步骤有_______________________________________。
【反思】(1)你能画出解一元二次不等式的解法的程序框图吗?
(2)对不等式,若方程
三种情形中,如何表示不等式的解集?
5、分式不等式的解法思想是___________________________________________
【反思】分式不等式可化为不等式组________________
6、一元高次不等式的解法思想是__________________________________________
简述用穿针引线法求一元高次不等式的解集的方法。
【反思】:在利用穿针引线法求一元高次不等式的解集的过程中,若出现因式,应如何处理?
【模拟试题】(答题时间:70分钟)
一、选择题:
1. 在△ABC中,已知a=1,b=,∠A=30°,B为锐角,则角A,B,C的大小关系是( )
A. A>B>C B. B>A>C C. C>B>A D. C>A>B
*2. 在△ABC中,角A,B满足:sin=sin,则三边a,b,c必满足( )
A. a=b B. a=b=c
C. a+b=2c D.
3. 如图,D,C,B三点在一条直线上,DC=a,从C,D两点测得A点的仰角是,()则A点离地面的高度AB 等于( )[来源:21世纪教育网]
4. 在三角形ABC中,下列等式总能成立的是( )
A. a cosC=c cosA B. bsinC=csinA C. absinc=bcsinB D. asinC=csinA
*5. 某人向正东方向走x千米后,他向右转150°,然后朝新的方向走3千米,结果他离出发点恰好为千米,则x=( )
*6. 有一座20米高的观测台,测得对面一水塔塔顶的仰角是60°,塔底的俯角是,则这座塔高是( )
*7. 已知两灯塔A和B与海洋观测站C的距离都是a km,灯塔A在观测站C的北偏东20°,灯塔B在观测站C的南偏东40°,则灯塔A与灯塔B的距离是( )
8. 在三角形ABC中,若(a+b+c)(b+c-a)=3bc,且sinA=2sinBcosC,则三角形ABC是( )
A. 等腰三角形, B. 等边三角形
C. 直角三角形 D. 等腰直角三角形
二、填空题:
*9. 在三角形ABC中,a-b=4,a+c=2b,且最大角为120°,则此三角形的周长是
**10. 在三角形ABC中,若C=3B,则的取值范围是
*11. 在三角形ABC中,已知B=45°,C=60°,则三角形的面积S=________
12. 海上有A,B两个小岛相距10海里,从A岛望,C岛和B岛成60°视角,从B岛望A岛和C岛成75°视角,则B岛和C岛的距离是 海里
*13. 在三角形ABC中,若acosA+bcosB=c cosC,则三角形ABC的形状是
**14. 若等腰三角形的顶角是20°,底边和一腰长分别是b,a,则下列结论不成立的是[来源:21世纪教育网]
(1),(3)(4)
三、计算题:
*15. 已知地面上有一旗杆OP,为了测得其高度h,地面上取一基线AB,AB=20米,在A处测得P点的仰角∠OAP=30°,在B处测得P点的仰角∠OBP=45°,又知∠AOB=60°,求旗杆的高度h.
16. 已知小岛A的周围38海里内有暗礁,船正向南航行,在B处测得小岛A在船的南偏东30°,航行30海里后在C处测得小岛A在船的南偏东45°,如果此船不改变航向,继续向南航行,问有无触礁的危险?
**17. 在圆心角为60°的扇形铁板OAB中,工人师傅要裁出一个面积最大的内接矩形,求此内接矩形的最大面积。
21世纪教育网
【试题答案】
一、选择题: C D A D C B B B
二、填空题:
9. 30 10.(1,3) 11. 12.
13. 直角三角形 14.(2)(3)(4)
三、计算题:
15.【分析】欲求旗杆的高度,只要注意到OP=OB=h.然后利用正弦定理或余弦定理解决即可。
解:AO=OPcot30°=,OB=OP=h,在三角形ABO中:由余弦定理得:
60°
答:所求旗杆的高度是。
16.【分析】要判断船有无触礁的危险,只要判断A到BC的直线距离是否大于38海里就可以判断。
解:在三角形ABC中:BC=30,∠B=30°,∠ACB=180°-45°=135°,故∠A=
15°
由正弦定理得:
故
于是A到BC的直线距离是Acsin45°==
,大于38海里。
答:继续向南航行无触礁的危险。
17. 【分析】要找出内接矩形的长宽与面积S的关系,可采用引入第三个变量的办法,用表示矩形的长宽x,y,这样矩形的面积可以表示成的三角函数,通过的变化情况,得出S的最大值。
解:如图,设PQ=x,MP=y,则矩形面积S=xy
连接ON,令∠AON=,则y=Rsin
在三角形OMN中:由正弦定理得:
故当=30°时,矩形的面积最大,其最大值是.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第二章 第2-3节 三角形中的几何计算;解三角形的实际应用举例(文)北师大版必修5
【本讲教育信息】
一、教学内容:
三角形中的几何计算及实际应用举例
二、教学目标
(1)体会用正弦定理、余弦定理处理三角形中的计算问题。
(2)能灵活的运用正弦定理、余弦定理解决测量、航海、台风预报等有关的实际问题,体会建立三角函数模型的思想。
(3)结合正弦定理、余弦定理等体会用方程的数学思想、分论讨论的数学思想等解决实际问题。
三、知识要点分析:
1. 三角形中的几何计算的有关知识点(三角形中的边和角的关系:)
(i)大角对大边:
(ii)正弦定理:,(R是三角形外接圆的半径)
(iii)余弦定理:
(iv)三角形的面积
S△ABC
2. 解决实际问题的有关知识点
(1)仰角与俯角:在视线与水平线所成的角中,视线在水平线上方的角叫仰角,视线在水平线下方的角叫俯角。
(2)方位角:指从正北方向顺时针转到目标方向线的夹角叫方位角。
(3)解决实际问题的步骤。
(i)理解题意分清已知与未知。(ii)画图建模利用正、余弦定理等知识点求解。(iii)作答。
3. 掌握三角形内角诱导公式及相关的结论,(i)tanA+tanB+tanC=tanAtanBtanC
(ii)
(iii)
【典型例题】
考点一:三角形中的几何计算
例1. 设D是直角三角形ABC的斜边BC上的一点,AB=AD,。
(1)求证:,(2)若求的值。
思路分析:(1)由已知找出与的关系,即,即可证明。(2)由正弦定理得到关于的方程即可。
解:(1)由AB=AD
.
①
(2)由正弦定理得:
将此式代入①得:
②
将②整理得:
又
故。即所求的角是
例2. 设P是正方形ABCD内一点,P到A、B、C的距离分别是1,2,3,求正方形ABCD的边长
思路分析:设正方形的边长为x,根据角ABP与角CBP互余,可知其余弦的平方和是1,建立关于x的方程,再求解。21世纪教育网
解:设边长是x,(1
同理在△CBP中: ,90°得:
即有: (*)
解*得所求的边长为。
说明:使用正弦定理或余弦定理或相关的知识点解决几何问题,首先要在已知的图形中构造三角形(已有三角形,不需构造),能构造特殊三角形的尽可能地构造特殊的三角形。
考点二:研究几何计算问题中的最值问题。
如图所示,点P在直径AB=1的半圆上移动,过点P作半圆的切线PT,使PT=1,则如何确定P点的位置?才能使得四边形ABTP的面积最大?
思路分析:由已知得P点的变化引起角PAB的变化,故可把四边形ABTP的面积表示成关于角PAB的函数,然后求函数的最值。
解:连接BP,设∠PAB=α,由AB为直径得∠APB=90°,即△APB是直角三角形,
由AB=PT=1得:。又PT是圆的切线,故,∠BPT=∠PAB=α
例4. 在等边三角形ABC中,AB=a,O为中心,过O的直线交AB于M,交AC于N,
求的最大值。
思路分析:由于M、N的变化导致角MOA的变化,然后利用正弦定理,把式子表示成角MOA的函数,再求最大值。
解:由已知∠MAO=∠NAO=30°,设∠MOA=θ,则
故当时,即时,取得最大值是。
【说明】在三角形几何计算中解决最值问题的关键是引入变量。
考点三:利用正弦定理、余弦定理解决实际问题
例5. (1)(航海问题)已知一测高仪表失灵的飞机在高空以300km/h的速度按水平方向向东飞行,飞机的航线和山顶C在同一铅直的平面内,若在A处的飞行员利用测角仪器测得先看到海拔高度为4000m的山顶C的俯角为15°,经120秒后在B点又看到山顶C的俯角是60°,求飞机现在的海拔高度。
思路分析:先根据已知条件画出图形,找出两个俯角,再根据正弦定理求出BC,在直角三角形BCD中求出CD,CD加上山的高度即是飞机现在的海拔高度。
解:根据已知画出图形(如图)∠BAC=15°,∠DBC=60°,故∠BCA=45°
又AB=300×=10(km),则在△ABC中由正弦定理得:
在直角△BDC中:CD=BCsin60°=
故飞机飞行的海拔高度是3170+4000=7170(米)
(2)某渔轮在航行中不幸遇险,发出呼救信号,我海军舰艇在A处获悉后,测出该渔轮在方位角45°,距离为10海里的C处,并测得渔轮正沿方位角为105°的方向,以每小时9海里的速度向小岛B靠拢,我海军舰艇立即以每小时21海里的速度前去营救,求舰艇的航向及靠近渔轮的时间。
思路分析:根据题意先画出图形,设舰艇收到信号后x小时在B处靠拢渔轮,在三角形ABC中利用余弦定理可求得x,再用正弦定理求得舰艇的航向。
解:设舰艇收到信号x小时在B处与渔轮靠拢,则AB=21x,BC=9x,AC=10,∠ACB=
120°
在△ABC中,由余弦定理得:120°
整理得:,由正弦定理可求∠BAC≈
21.8°,
答:舰艇沿方位角(45°+21.8°)的方向航行40min 可靠近渔轮。
例6. (测量问题)欲测量河对岸两点P,Q之间的距离,应如何测量?
思路分析:可以在岸边选定距离为a的两个观测点A,B,然后测出角BAP,角BAQ,角ABQ,角ABP,利用正弦定理求解。
解:选定距离为a的两个观测点A,B。利用测角仪器测得:∠BAP=∠BAQ=,∠ABQ=
∠ABP=,则由正弦定理得:,
同理:,在三角形APQ中利用余弦定理得:
例7. (台风问题)某城市附近的海面上有一股台风,台风中心位于城市O的南偏东方向300km海面的P处,并以每小时20km/h的速度向北偏西45°的方向移动,台风侵袭的范围为圆形区域,当时半径是60km,并以10km/h的速度不断增大,问几小时后该城市受到台风的侵袭?21世纪教育网
思路分析:设经过x小时该城市恰好受到台风的侵袭,假设台风中心由P移到Q处(如图),此时台风的侵袭半径是OQ=60+10x,在三角形OPQ中,OP=300,PQ=20x,由余弦定理建立关于x的方程求x。
解:设x小时后该城市恰好受到台风的侵袭,此时台风中心由P处移到Q处,台风的侵袭半径是(60+10x)km,城市O恰好受到台风侵袭的条件是OQ=60+10x
在三角形OPQ中:OP=300,PQ=20x,∠OPQ=-45°,cos∠OPQ=cos(-45°)
=,
由余弦定理得:
故方程无解,即该城市不会受到台风的影响。
【本讲涉及的数学思想、方法】
本讲主要讲述了利用正弦定理、余弦定理及其相关的知识解决三角形中的几何计算及实际问题,在此过程中,体现了方程的数学思想(如例1、例2)、函数的数学思想(如求最值问题)、等价转化的数学思想等在解题中的应用。
预习导学案
(不等关系及一元二次不等式的解法)
一:预习前知
1. 在初中你学过不等式有哪些性质?
2. 解一元一次不等式的步骤有哪些?
3. 解关于x的不等式:ax>b (a,b是实数)
4. 二次函数的关系是什么?
二:预习导学
探究、反思
探究反思的任务:不等关系、一元二次不等式的解法
1、举例说明在现实生活中的不等关系。
【反思】比较两个实数大小的方法有哪些?(作差比较,作商比较)
a-b>0
2、不等式的性质有哪些?
传递性_________,(2)加法单调性_________,(3)乘法单调性_________。(4)同向不等式相加______________(5)两边都是正数的同向不等式相乘_____________。
【反思】由上面的性质你能证明:a>b>0,吗?
3、一元二次不等式的定义:_____________________________________________。
4、一元二次不等式的解法的步骤有_______________________________________。
【反思】(1)你能画出解一元二次不等式的解法的程序框图吗?
(2)对不等式,若方程
三种情形中,如何表示不等式的解集?
5、分式不等式的解法思想是___________________________________________
【反思】分式不等式可化为不等式组________________
6、一元高次不等式的解法思想是__________________________________________
简述用穿针引线法求一元高次不等式的解集的方法。
【反思】:在利用穿针引线法求一元高次不等式的解集的过程中,若出现因式,应如何处理?
【模拟试题】(答题时间:70分钟)
一、选择题:
1. 在△ABC中,已知a=1,b=,∠A=30°,B为锐角,则角A,B,C的大小关系是( )
A. A>B>C B. B>A>C C. C>B>A D. C>A>B
*2. 在△ABC中,角A,B满足:sin=sin,则三边a,b,c必满足( )
A. a=b B. a=b=c
C. a+b=2c D.
3. 如图,D,C,B三点在一条直线上,DC=a,从C,D两点测得A点的仰角是,()则A点离地面的高度AB 等于( )[来源:21世纪教育网]
4. 在三角形ABC中,下列等式总能成立的是( )
A. a cosC=c cosA B. bsinC=csinA C. absinc=bcsinB D. asinC=csinA
*5. 某人向正东方向走x千米后,他向右转150°,然后朝新的方向走3千米,结果他离出发点恰好为千米,则x=( )
*6. 有一座20米高的观测台,测得对面一水塔塔顶的仰角是60°,塔底的俯角是,则这座塔高是( )
*7. 已知两灯塔A和B与海洋观测站C的距离都是a km,灯塔A在观测站C的北偏东20°,灯塔B在观测站C的南偏东40°,则灯塔A与灯塔B的距离是( )
8. 在三角形ABC中,若(a+b+c)(b+c-a)=3bc,且sinA=2sinBcosC,则三角形ABC是( )
A. 等腰三角形, B. 等边三角形
C. 直角三角形 D. 等腰直角三角形
二、填空题:
*9. 在三角形ABC中,a-b=4,a+c=2b,且最大角为120°,则此三角形的周长是
**10. 在三角形ABC中,若C=3B,则的取值范围是
*11. 在三角形ABC中,已知B=45°,C=60°,则三角形的面积S=________
12. 海上有A,B两个小岛相距10海里,从A岛望,C岛和B岛成60°视角,从B岛望A岛和C岛成75°视角,则B岛和C岛的距离是 海里
*13. 在三角形ABC中,若acosA+bcosB=c cosC,则三角形ABC的形状是
**14. 若等腰三角形的顶角是20°,底边和一腰长分别是b,a,则下列结论不成立的是[来源:21世纪教育网]
(1),(3)(4)
三、计算题:
*15. 已知地面上有一旗杆OP,为了测得其高度h,地面上取一基线AB,AB=20米,在A处测得P点的仰角∠OAP=30°,在B处测得P点的仰角∠OBP=45°,又知∠AOB=60°,求旗杆的高度h.
16. 已知小岛A的周围38海里内有暗礁,船正向南航行,在B处测得小岛A在船的南偏东30°,航行30海里后在C处测得小岛A在船的南偏东45°,如果此船不改变航向,继续向南航行,问有无触礁的危险?
**17. 在圆心角为60°的扇形铁板OAB中,工人师傅要裁出一个面积最大的内接矩形,求此内接矩形的最大面积。
21世纪教育网
【试题答案】
一、选择题: C D A D C B B B
二、填空题:
9. 30 10.(1,3) 11. 12.
13. 直角三角形 14.(2)(3)(4)
三、计算题:
15.【分析】欲求旗杆的高度,只要注意到OP=OB=h.然后利用正弦定理或余弦定理解决即可。
解:AO=OPcot30°=,OB=OP=h,在三角形ABO中:由余弦定理得:
60°
答:所求旗杆的高度是。
16.【分析】要判断船有无触礁的危险,只要判断A到BC的直线距离是否大于38海里就可以判断。
解:在三角形ABC中:BC=30,∠B=30°,∠ACB=180°-45°=135°,故∠A=
15°
由正弦定理得:
故
于是A到BC的直线距离是Acsin45°==
,大于38海里。
答:继续向南航行无触礁的危险。
17. 【分析】要找出内接矩形的长宽与面积S的关系,可采用引入第三个变量的办法,用表示矩形的长宽x,y,这样矩形的面积可以表示成的三角函数,通过的变化情况,得出S的最大值。
解:如图,设PQ=x,MP=y,则矩形面积S=xy
连接ON,令∠AON=,则y=Rsin
在三角形OMN中:由正弦定理得:
故当=30°时,矩形的面积最大,其最大值是.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
