(北师大版必修5)数学:第二章《解三角形周末作业》测试
文档属性
| 名称 | (北师大版必修5)数学:第二章《解三角形周末作业》测试 |

|
|
| 格式 | rar | ||
| 文件大小 | 58.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-28 00:00:00 | ||
图片预览

文档简介
解三角形周末作业
1.△ABC中,D在边BC上,且BD=2,DC=1,∠B=60o,∠ADC=150o,求AC的长及△ABC的面积.
2.在△ABC中,已知角A,B,C的对边分别为a,b,c,且bcosB+ccosC=acosA,试判断△ABC的形状.
3. 如图,海中有一小岛,周围3.8海里内有暗礁。一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北端东60°。若此舰不改变舰行的方向继续前进,问此舰有没有角礁的危险?21世纪教育网
21世纪教育网
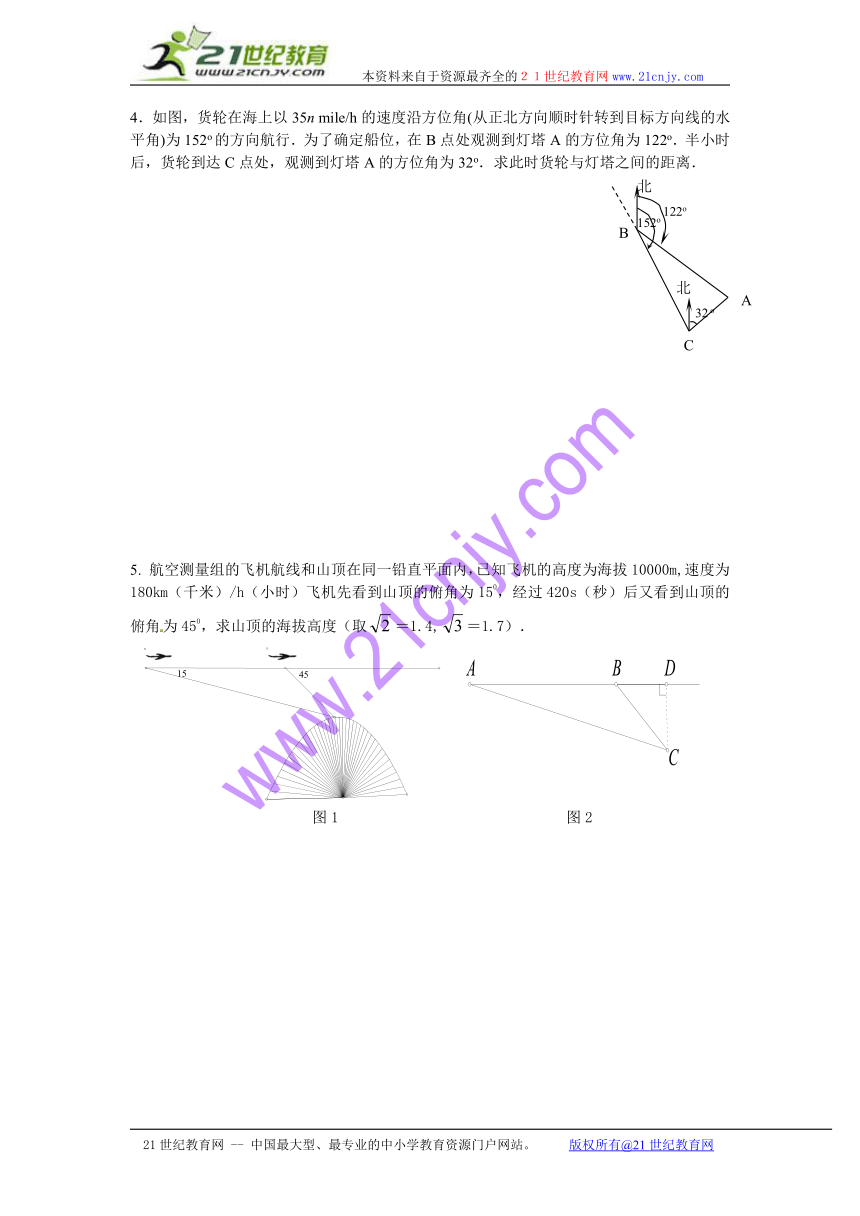
4.如图,货轮在海上以35n mile/h的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为152o的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为122o.半小时后,货轮到达C点处,观测到灯塔A的方位角为32o.求此时货轮与灯塔之间的距离.21世纪教育网
5. 航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10000m,速度为180km(千米)/h(小时)飞机先看到山顶的俯角为150,经过420s(秒)后又看到山顶的俯角为450,求山顶的海拔高度(取=1.4,=1.7).
[来源:21世纪教育网]
图1 图2
6. 在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南
方向300km的海面P处,并以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时?
参考答案
1.在△ABC中,∠BAD=150o-60o=90o,∴AD=2sin60o=.
在△ACD中,AD2=()2+12-2××1×cos150o=7,∴AC=.
∴AB=2cos60o=1.S△ABC=×1×3×sin60o=.
2.∵ bcosB+ccosC=acosA,由正弦定理得:sinBcosB+sinCcosC=sinAcosA,
即sin2B+sin2C=2sinAcosA,∴2sin(B+C)cos(B-C)=2sinAcosA.∵A+B+C=π,
∴sin(B+C)=sinA.而sinA≠0,∴cos(B-C)=cosA,即cos(B-C)+cos(B+C)=0,
∴2cosBcosC=0.∵ 0<B<π,0<C<π,∴B=或C=,即△ABC是直角三角形.
3、解:如图,过点B作BD⊥AE交AE于D
由已知,AC=8,∠ABD=75°,∠CBD=60°
在Rt△ABD中,
AD=BD·tan∠ABD=BD·tan 75°
在Rt△CBD中,
CD=BD·tan∠CBD=BD·tan60°
∴AD-CD=BD(tan75°-tan60°)=AC=8,…9分∴
∴该军舰没有触礁的危险。
4.在△ABC中,∠B=152o-122o=30o,∠C=180o-152o+32o=60o,∠A=180o-30o-60o=90o,BC=,∴AC=sin30o=.
答:船与灯塔间的距离为n mile.
5. 解:如图 ∵150 450
∴300,
AB= 180km(千米)/h(小时)420s(秒)
= 21000(m )
∴在中
∴
∴
∵,
∴
=
==
=7350
山顶的海拔高度=10000-7350=2650(米)
6.解:设经过t小时台风中心移动到Q点时,台风边沿恰经过O城,
由题意可得:OP=300,PQ=20t,OQ=r(t)=60+10t
因为,α=θ-45°,所以,
由余弦定理可得:OQ2=OP2+PQ2-2·OP·PQ·21世纪教育网
即 (60+10t)2=3002+(20t)2-2·300·20t·
即,
解得,
答:12小时后该城市开始受到台风气侵袭,受到台风的侵袭的时间有12小时?
1.△ABC中,D在边BC上,且BD=2,DC=1,∠B=60o,∠ADC=150o,求AC的长及△ABC的面积.
2.在△ABC中,已知角A,B,C的对边分别为a,b,c,且bcosB+ccosC=acosA,试判断△ABC的形状.
3. 如图,海中有一小岛,周围3.8海里内有暗礁。一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北端东60°。若此舰不改变舰行的方向继续前进,问此舰有没有角礁的危险?21世纪教育网
21世纪教育网
4.如图,货轮在海上以35n mile/h的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为152o的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为122o.半小时后,货轮到达C点处,观测到灯塔A的方位角为32o.求此时货轮与灯塔之间的距离.21世纪教育网
5. 航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10000m,速度为180km(千米)/h(小时)飞机先看到山顶的俯角为150,经过420s(秒)后又看到山顶的俯角为450,求山顶的海拔高度(取=1.4,=1.7).
[来源:21世纪教育网]
图1 图2
6. 在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南
方向300km的海面P处,并以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时?
参考答案
1.在△ABC中,∠BAD=150o-60o=90o,∴AD=2sin60o=.
在△ACD中,AD2=()2+12-2××1×cos150o=7,∴AC=.
∴AB=2cos60o=1.S△ABC=×1×3×sin60o=.
2.∵ bcosB+ccosC=acosA,由正弦定理得:sinBcosB+sinCcosC=sinAcosA,
即sin2B+sin2C=2sinAcosA,∴2sin(B+C)cos(B-C)=2sinAcosA.∵A+B+C=π,
∴sin(B+C)=sinA.而sinA≠0,∴cos(B-C)=cosA,即cos(B-C)+cos(B+C)=0,
∴2cosBcosC=0.∵ 0<B<π,0<C<π,∴B=或C=,即△ABC是直角三角形.
3、解:如图,过点B作BD⊥AE交AE于D
由已知,AC=8,∠ABD=75°,∠CBD=60°
在Rt△ABD中,
AD=BD·tan∠ABD=BD·tan 75°
在Rt△CBD中,
CD=BD·tan∠CBD=BD·tan60°
∴AD-CD=BD(tan75°-tan60°)=AC=8,…9分∴
∴该军舰没有触礁的危险。
4.在△ABC中,∠B=152o-122o=30o,∠C=180o-152o+32o=60o,∠A=180o-30o-60o=90o,BC=,∴AC=sin30o=.
答:船与灯塔间的距离为n mile.
5. 解:如图 ∵150 450
∴300,
AB= 180km(千米)/h(小时)420s(秒)
= 21000(m )
∴在中
∴
∴
∵,
∴
=
==
=7350
山顶的海拔高度=10000-7350=2650(米)
6.解:设经过t小时台风中心移动到Q点时,台风边沿恰经过O城,
由题意可得:OP=300,PQ=20t,OQ=r(t)=60+10t
因为,α=θ-45°,所以,
由余弦定理可得:OQ2=OP2+PQ2-2·OP·PQ·21世纪教育网
即 (60+10t)2=3002+(20t)2-2·300·20t·
即,
解得,
答:12小时后该城市开始受到台风气侵袭,受到台风的侵袭的时间有12小时?
