(苏教版必修1)函数的概念与图像(2)
图片预览








文档简介
课件22张PPT。2.1.1函数的概念和图象(二)回忆:函数的定义是怎样的?它有几个要
素?分别是什么? 函数的定义 设A、B是非空的数集,如果按照某种对应
法则f,对于集合A中的每一个元数x,在集合B中
都有惟一的元素y和它对应,这样的对应叫做
从A到B的一个函数,通常记为 y=f(x),x∈A 其中,所有的输入值x组成的集合A叫做函数的
定义域 .非空每一个惟一函数的三要素:
定义域、值域、对应关系
(定义域→优先,对应法则→核心)练习:求下列函数的定义域
;。回忆:
在初中我们是采用什么方法来画出函数的图象? 列表、描点、连线 描点法描点法作图的步骤有哪些?⑴f(x)=x+1
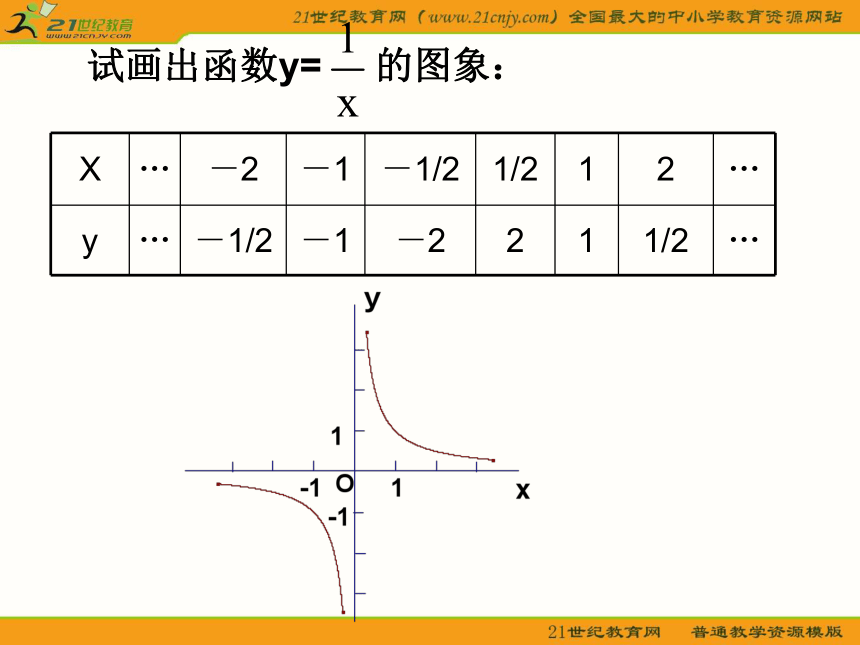
⑵f(x)=(x-1)2+1,x∈[1,3) 例4试画出下列函数的图象: 试画出函数y= 的图象: 将自变量的一个值x0作为横坐标,相应的
函数值f(x0)作为纵坐标,就得到坐标平面上的
一个点(x0,f(x0)).当自变量取遍函数定义域A中
的每一个值时,就得到一系列这样的点.所有
这些点组成的集合(点集)为
{(x,f(x))|x∈A},
即
{(x,f(x))|y=f(x),x∈A},
所有这些点组成的图形就是函数y=f(x)的图象. ⑵一物体从静止开始下落,下落的距离y(m)与下落时
间x(s)之间近似地满足关系式y=4.9x2.作出它图像思考:设函数y=f(x)的定义域为A,则集
合P={(x,y)|y=f(x),x∈A}与集合
Q={y|y=f(x),x∈A}相等吗?请说明理由.问题:直线x=1和函数y=x2+1的图象的公共
点可能几个?变:⑴(P29习题6)直线x=a和函数y=x2+1
的图象的公共点可能几个? ⑵直线x=-1和函数y=x2+1 ,x∈[0.+∞)
的图象的公共点可能几个?⑶直线x=a和函数y=x2+1 ,x∈A的图象的
公共点可能几个? ⑷直线x=a和函数y=f(x),x∈A的图象的
公共点可能几个? 当a∈A,则根据图象知有且仅有一个公共点;
当a?A时,没有公共点. 例6 试画出函数f(x)=x2+1的图象,并根据图象
回答下列问题:
⑴比较f(-2),f(1),f(3)的大小;
⑵若0<x1<x2,试比较f(x1)与f(x2)的大小.思考:在上例⑵中,
⑴如果把“0<x1<x2”改为“x1<x2<0”,
那么f(x1)与f(x2)哪个大? ⑵如果把“0<x1<x2”改为“|x1|<|x2|”,
那么f(x1)与f(x2)哪个大? 1.已知函数f(x)=
(1)画出函数图象;
(2)求f{f[f(-2)]}
(3)求当f(x)= -7时,x的值;回顾反思 能用描点法画出常见函数的图象,
并能根据函数的图象解决有关问题.作业
P20习题2.1⑴7,8,9
素?分别是什么? 函数的定义 设A、B是非空的数集,如果按照某种对应
法则f,对于集合A中的每一个元数x,在集合B中
都有惟一的元素y和它对应,这样的对应叫做
从A到B的一个函数,通常记为 y=f(x),x∈A 其中,所有的输入值x组成的集合A叫做函数的
定义域 .非空每一个惟一函数的三要素:
定义域、值域、对应关系
(定义域→优先,对应法则→核心)练习:求下列函数的定义域
;。回忆:
在初中我们是采用什么方法来画出函数的图象? 列表、描点、连线 描点法描点法作图的步骤有哪些?⑴f(x)=x+1
⑵f(x)=(x-1)2+1,x∈[1,3) 例4试画出下列函数的图象: 试画出函数y= 的图象: 将自变量的一个值x0作为横坐标,相应的
函数值f(x0)作为纵坐标,就得到坐标平面上的
一个点(x0,f(x0)).当自变量取遍函数定义域A中
的每一个值时,就得到一系列这样的点.所有
这些点组成的集合(点集)为
{(x,f(x))|x∈A},
即
{(x,f(x))|y=f(x),x∈A},
所有这些点组成的图形就是函数y=f(x)的图象. ⑵一物体从静止开始下落,下落的距离y(m)与下落时
间x(s)之间近似地满足关系式y=4.9x2.作出它图像思考:设函数y=f(x)的定义域为A,则集
合P={(x,y)|y=f(x),x∈A}与集合
Q={y|y=f(x),x∈A}相等吗?请说明理由.问题:直线x=1和函数y=x2+1的图象的公共
点可能几个?变:⑴(P29习题6)直线x=a和函数y=x2+1
的图象的公共点可能几个? ⑵直线x=-1和函数y=x2+1 ,x∈[0.+∞)
的图象的公共点可能几个?⑶直线x=a和函数y=x2+1 ,x∈A的图象的
公共点可能几个? ⑷直线x=a和函数y=f(x),x∈A的图象的
公共点可能几个? 当a∈A,则根据图象知有且仅有一个公共点;
当a?A时,没有公共点. 例6 试画出函数f(x)=x2+1的图象,并根据图象
回答下列问题:
⑴比较f(-2),f(1),f(3)的大小;
⑵若0<x1<x2,试比较f(x1)与f(x2)的大小.思考:在上例⑵中,
⑴如果把“0<x1<x2”改为“x1<x2<0”,
那么f(x1)与f(x2)哪个大? ⑵如果把“0<x1<x2”改为“|x1|<|x2|”,
那么f(x1)与f(x2)哪个大? 1.已知函数f(x)=
(1)画出函数图象;
(2)求f{f[f(-2)]}
(3)求当f(x)= -7时,x的值;回顾反思 能用描点法画出常见函数的图象,
并能根据函数的图象解决有关问题.作业
P20习题2.1⑴7,8,9
