(苏教版必修1)函数的概念与图像(1)
文档属性
| 名称 | (苏教版必修1)函数的概念与图像(1) |  | |
| 格式 | rar | ||
| 文件大小 | 277.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-30 08:00:00 | ||
图片预览






文档简介
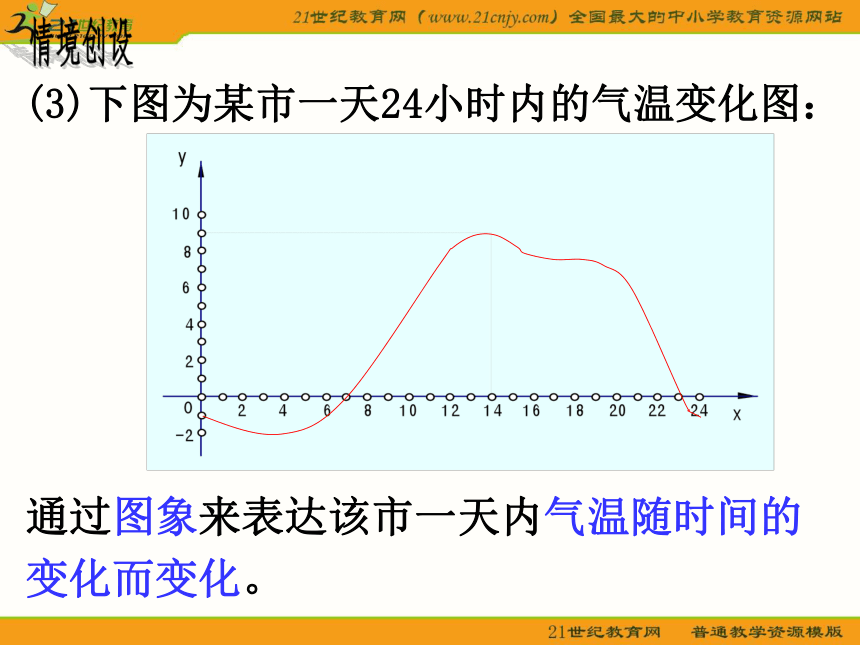
课件18张PPT。函数函数的概念问题2:什么叫做函数?问题1:初中我们学过哪些函数?复习回顾情境创设 通过1949—1999年来我国人口数据表体现了我国人口随年份的变化而变化.通过代数表达式来体现:下落距离随时间的变化而变化。情境创设情境创设(3)下图为某市一天24小时内的气温变化图:通过图象来表达该市一天内气温随时间的变化而变化。问题1三个问题涉及到的集合有什么共同点?
问题2这三个问题有什么共同特点? 在上述的每个问题中都含有两个变量,当一个变量的取值确定后,另一个变量的值随之确定。根据初中学过的知识,对应的两个变量之间形成的是 函数 关系。每一个问题都涉及两个非空数集A,B; 对于A中的每一个元素,按某种对应的规则在B中都有唯一的元素与之对应。AB年份人口(百万)建构数学这样的对应叫做从A到B的一个函数。函数的概念:一般地,设A,B是两个非空的数集,如果按照某种对应法则f, 对于集合A中的每一个元素x,在集合B中都有唯一的元素y和它对应,通常记为:y=f(x),x∈A. 函数是建立在两个非空数集上的单值对应,x称为自变量,y称为因变量。 其中,所有的输入值x组成的集合A称为函数y=f(x)的定义域。 而A中每一个输入值x都有一个输出值y与之对应,我们将所有的输出值y组成的集合称为值域。注意:2、构成函数的三要素: 定义域(集合A)、值域、对应法则(判断是否为同一函数只要看定义域、对应法则是否完全相同)。1、f不是函数而是对应法则,集合A、B与对应法则f连在一起才是从A到B的一个函数。3、函数定义域是使函数有意义的x的取值范围,所以函数中,必须分母不能为零,二次根式的被开方数(式)非负等等。4、集合B不一定是函数的值域,函数的值域是B的子集。值域与集合B的关系怎样?数学应用例1.判断下列对应是否为A到B的函数:车票1车票 2车票 3AB座位1座位2座位3(1)(3)A={1,2,3},B={4,5,6},f(1)=f(2)=4(4)A=B={1,2,3}, f(x)=x+1练习1.判断下列对应是否为函数.(4)x→y=x,x∈{x|0≤x≤6},y∈{y|0≤y≤3}(5)x→y= ,x∈{x|0≤x≤6},y∈{y|0≤y≤3} 一般地,设A,B是两个 ,如果按照某种对应法则f,对于集合A中的 , 在集合B中都有 和它对应 ,这样的
叫做从A到B的一个函数。非空的数集每一个元素x 唯一的元素y对应(2){x|x≠2, x∈R }(4){x|x>3}数学应用(3){x|x≥1,且x≠2}小结:常见函数求定义域时注意点例3.判断下列各组函数是否为同一函数:(1)y=2x+1, y=3x+1(2)f(x)=2x+1, g(t)=2t+1(3)f(x)=x+1, g(x)=注:若两个函数的对应法则与定义域均相同,则这两个函数为同一函数。数学应用练习:下列函数中哪个与函数y=x是同一个函数?定义域不同 对应法则不同数学应用知识回顾1、函数的概念;(一种特殊的对应)2、函数定义域的求解;(自变量的取值范围)3、同一函数的判定。(对应法则、定义域)作业:学案。思考:函数f(x)=1的定义域是________ 数学中的转折点是笛卡尔的变数,有了变数,运动就进入了数学;有了变数,辩证法就进入了数学。——恩格斯
问题2这三个问题有什么共同特点? 在上述的每个问题中都含有两个变量,当一个变量的取值确定后,另一个变量的值随之确定。根据初中学过的知识,对应的两个变量之间形成的是 函数 关系。每一个问题都涉及两个非空数集A,B; 对于A中的每一个元素,按某种对应的规则在B中都有唯一的元素与之对应。AB年份人口(百万)建构数学这样的对应叫做从A到B的一个函数。函数的概念:一般地,设A,B是两个非空的数集,如果按照某种对应法则f, 对于集合A中的每一个元素x,在集合B中都有唯一的元素y和它对应,通常记为:y=f(x),x∈A. 函数是建立在两个非空数集上的单值对应,x称为自变量,y称为因变量。 其中,所有的输入值x组成的集合A称为函数y=f(x)的定义域。 而A中每一个输入值x都有一个输出值y与之对应,我们将所有的输出值y组成的集合称为值域。注意:2、构成函数的三要素: 定义域(集合A)、值域、对应法则(判断是否为同一函数只要看定义域、对应法则是否完全相同)。1、f不是函数而是对应法则,集合A、B与对应法则f连在一起才是从A到B的一个函数。3、函数定义域是使函数有意义的x的取值范围,所以函数中,必须分母不能为零,二次根式的被开方数(式)非负等等。4、集合B不一定是函数的值域,函数的值域是B的子集。值域与集合B的关系怎样?数学应用例1.判断下列对应是否为A到B的函数:车票1车票 2车票 3AB座位1座位2座位3(1)(3)A={1,2,3},B={4,5,6},f(1)=f(2)=4(4)A=B={1,2,3}, f(x)=x+1练习1.判断下列对应是否为函数.(4)x→y=x,x∈{x|0≤x≤6},y∈{y|0≤y≤3}(5)x→y= ,x∈{x|0≤x≤6},y∈{y|0≤y≤3} 一般地,设A,B是两个 ,如果按照某种对应法则f,对于集合A中的 , 在集合B中都有 和它对应 ,这样的
叫做从A到B的一个函数。非空的数集每一个元素x 唯一的元素y对应(2){x|x≠2, x∈R }(4){x|x>3}数学应用(3){x|x≥1,且x≠2}小结:常见函数求定义域时注意点例3.判断下列各组函数是否为同一函数:(1)y=2x+1, y=3x+1(2)f(x)=2x+1, g(t)=2t+1(3)f(x)=x+1, g(x)=注:若两个函数的对应法则与定义域均相同,则这两个函数为同一函数。数学应用练习:下列函数中哪个与函数y=x是同一个函数?定义域不同 对应法则不同数学应用知识回顾1、函数的概念;(一种特殊的对应)2、函数定义域的求解;(自变量的取值范围)3、同一函数的判定。(对应法则、定义域)作业:学案。思考:函数f(x)=1的定义域是________ 数学中的转折点是笛卡尔的变数,有了变数,运动就进入了数学;有了变数,辩证法就进入了数学。——恩格斯
