（苏教版必修1）1.3交集、并集

课件29张PPT。1.3交集、并集思考： 两个实数除了可以比较大小外，还可以进行加减运算，类比实数的加法运算，两个集合是否也可以“相减”呢？引入1： 考察下面的问题，集合C与集合A、B之间有什么关系吗？（1） A=｛2，4，6，8，10｝， B=｛3，5，8，12｝，C=｛8｝． 集合C是由那些既属于集合A且又属于集合B的所有元素组成的．（2）A={x|x是等腰三角形}，B= {x|x是直角三角形}，C= {x|x是等腰直角三角形}，
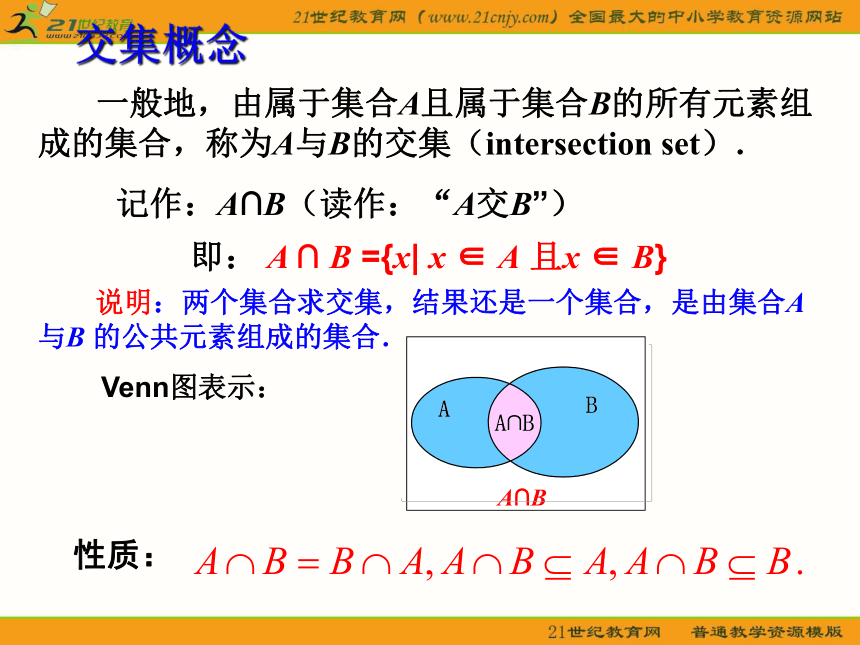
一般地，由属于集合A且属于集合B的所有元素组成的集合，称为A与B的交集（intersection set）．记作：A∩B（读作：“A交B”）
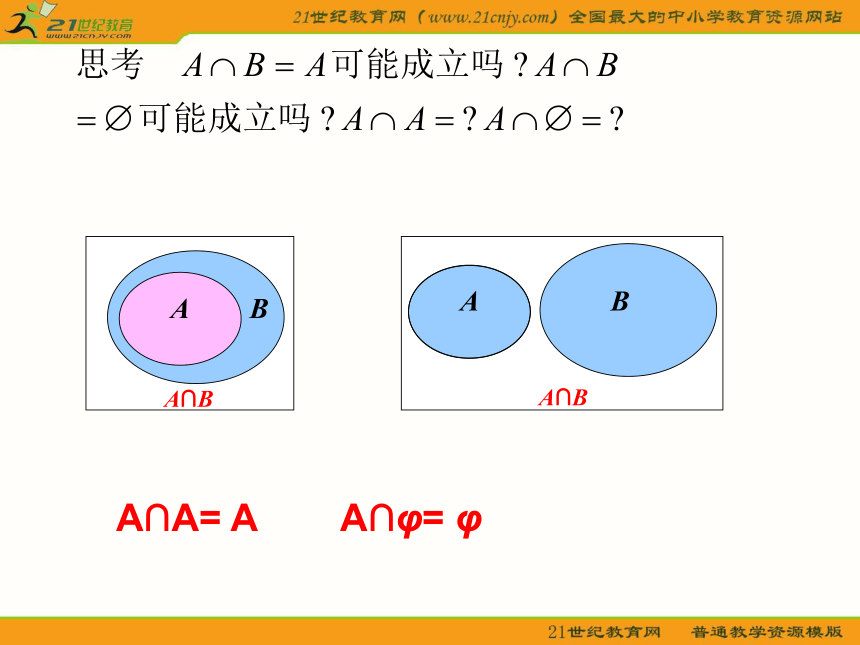
即： A ∩ B ={x| x ∈ A 且x ∈ B}Venn图表示： 说明：两个集合求交集，结果还是一个集合，是由集合A与B 的公共元素组成的集合．交集概念性质：A∩A= A A∩φ= φ引入2： 考察下列各个集合，你能说出集合C与集合A、B之间的关系吗？（1） A=｛1，3，5｝， B=｛2，4，6｝，
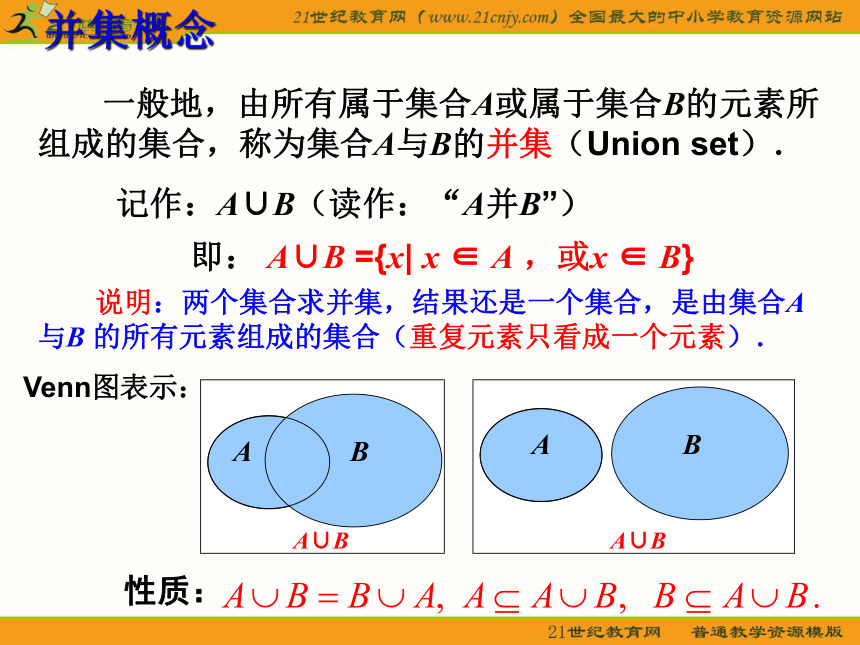
C=｛1，2，3，4，5，6｝．（2）A=｛x|x是有理数｝， B=｛x|x是无理数｝，C=｛x|x是实数｝． 集合C是由所有属于集合A或属于B的元素组成的． 一般地，由所有属于集合A或属于集合B的元素所组成的集合，称为集合A与B的并集（Union set）．记作：A∪B（读作：“A并B”）
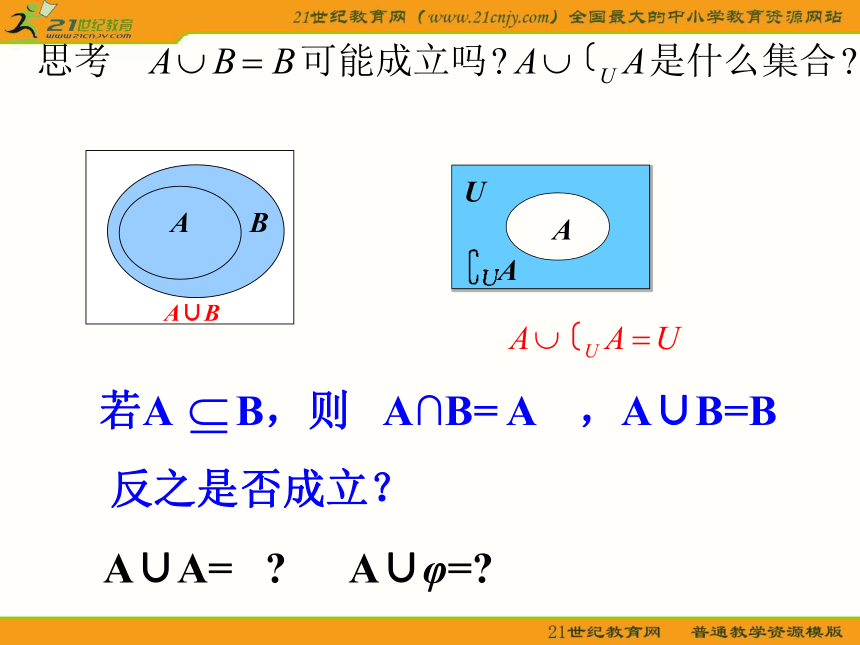
即： A∪B ={x| x ∈ A ，或x ∈ B}Venn图表示： 说明：两个集合求并集，结果还是一个集合，是由集合A与B 的所有元素组成的集合（重复元素只看成一个元素）．并集概念性质： A∪A= ? A∪φ=? 若A B，则 A∩B= A ，A∪B=B反之是否成立？ 例题讲评例4：设A={x|－1≤x≤2}，B={x|1求（1）A∩B （2）A∪B
练习：P13 1~5 小结、作业布置= { 5，8 }，= {3，4，5，6，7，8};练习 1：= { x | 0≤x<5 }.={x| x>-2 }.= {x | x是平行四边形}.例5 设A={(x，y)| y=-4x+6}，
B={(x，y)|y=5x-3}，求A∩B.
解：
A∩B= {(x，y)|y=-4x+6}∩{(x，y)|y=5x-3}
={(1，2)}.例6 已知A为奇数集，B为偶数集，Z为整数集，求 A∩B，A∩Z，B∩Z，
A∪B，A∪Z，B∪Z .
解： A∩B ={奇数}∩{偶数}=φ，
A∩Z ={奇数}∩Z ={奇数}=A，
B∩Z ={偶数}∩Z ={偶数}=B，
A∪B ={奇数}∪{偶数}=Z，
A∪Z ={奇数}∪Z =Z，
B∪Z ={偶数}∪Z =Z .解:∵ (CUA) ={1，2，6，7，8}，
(CUB) ={1，2，3，5，6}，
∴(CUA)∩(CUB) ={1，2，6}，
(CUA)∪(CUB) ={1,2,3,5,6,7,8}，
∵A∪B={3，4，5 ，7，8} , A ∩B={4}
∴ CU (A∪B) = {1，2，6}，
CU (A ∩B) = {1,2,3,5,6,7,8}.例7.设U={1，2，3，4，5，6，7，8}，
A={3，4，5}，B={4，7，8}，
求 (CUA)∩(CUB)， (CUA)∪(CUB) ，
CU (A∪B)， CU (A ∩B) .摩根定律：(CUA)∩(CUB) = CU (A∪B)
(CUA)∪(CUB) = CU (A∩B) 练习 2：解：A∩B ={(1，-1)}，A∩D = {(x，y)|3x+2y=1}.B∩C =φ，A∩B=A∩D=C∩B= C∩D=φ.A=C，B=D，解：CU (A∩B) = {1，2，4，5，6，7，8}.∴ A∩B = {3}，解：(CUA)∪ (CUB)= CU(A∩B)(CUA)∩(CUB)= CU(A∪B)解：AA∩BB解：ABABBA∪BB∪AAAAAUU