(苏教版必修1)1.2子集、全集、补集
图片预览






文档简介
课件19张PPT。1.2子集、全集、补集ks5u精品课件温故而知新ks5u精品课件类比实数的大小关系,如5<7,2≤2,
试想集合间是否有类似的“大小”关系呢? 温故而知新ks5u精品课件问题1.观察下列各组集合,A与B具有怎样的
关系?如何用数学语言来表达这种关系?
⑴A={-1,1}, B={-1,0,1,2}
⑵A=N,B=R
⑶A={x|x为高一⑶班的男生},
B={y|y为高一⑶班的学生}
⑷A={x|x为江苏人},
B={y|y为中国人}
ks5u精品课件1.集合与集合之间的“包含”关系 如果集合A的任何一个元素都是集合B的元
素,则称集合A是集合B的子集(subset),
记为A?B或B?A,读作:A包含于(is
contained in)集合B”,或“集合B包含
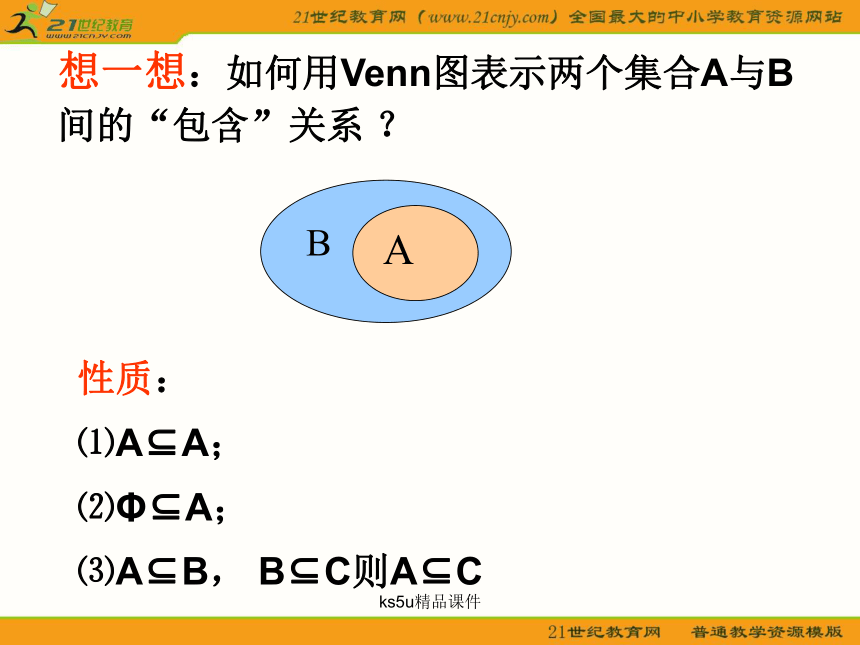
(contains)集合A”.子集的定义ks5u精品课件想一想:如何用Venn图表示两个集合A与B
间的“包含”关系 ?性质:
⑴A?A;
⑵Φ?A;
⑶A?B, B?C则A?Cks5u精品课件想一想:
A?B与B?A能否同时成立?
你能举出一个例子吗? 2.集合与集合之间的 “相等”关系:
若A?B且B?A ,则A=B. ks5u精品课件3.真子集的概念
若集合A?B,存在元素x∈B且x?A,则称集
合A是集合B的真子集(proper subset)。
记作:A B(或BA)读作:A真包含于 B(或B真包含A) 性质:
⑴ A≠Φ,则Φ A;
⑶A B, B C则A Cks5u精品课件例1写出集合{a,b}的所有的子集. 解析:?,{a},{b},{a,b} 变:写出集合{a,b,c}的所有的子集. 解析:?,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}猜想:
若A中有n个元素,A的子集有_____ 个.
若A中有n个元素,A的真子集有_____ 个2n 2n-1 ks5u精品课件练习:1.判断下列说法是否正确: (2)空集是任何集合的真子集; ( × )( × )( × )( × )( × )( √ )ks5u精品课件练习:=ks5u精品课件例2下列三个集合中,哪两个集合具有包含关系?
⑴S={―2,―1,1,2},A={―1,1},B={―2,2};
⑵S=R,A={x|x≤0,x∈R},B={x|x>0,x∈R};
⑶S={x|x为地球人},A={x|x为中国人},
B={x|x为外国人}.思考:观察例2中每一组的三个集合,它们
之间还有一种什么关系? ks5u精品课件 4.补集的概念
补集的定义:设A?S,由S中不属于A的所
有元素组成的集合称为S的子集A的补集
complementary set),简称为集合A的补集,
记作:CsA(读作A在S中的补集)即:
CsA={x|x∈S且x?A}. 5.全集的概念
全集的定义:如果集合S包含我们所要
研究的各个集合这时S可以看着一个全集,
通常记为U.ks5u精品课件想一想:如何用Venn图表示CU A?想一想:CUA在U中的补集等于什么?CU(CUA)=Aks5u精品课件例3 不等式组 的解集为A,U=R,试求A及CUA,并把
它们分别表示在数轴上. 点评:不等式问题通常借助数轴来研究,
但要注意实心点与空心点. ks5u精品课件学生练习:
A组P9练习3,4
ks5u精品课件回顾反思 1.两个集合之间的关系有“包含”、“相等” 、“真包含”、 “不包含” 几种,,同时还要注意区别元素与集合关系及其表示方法.
2.补集的概念必须要有全集的限制.
3.充分利用“形”来解决问题. ks5u精品课件2.预习提纲:
(1)交集与并集的含义是什么?能否说明?
(2)求两个集合交集或并集时如何借助图形.作业1.课后作业:P10习题1,2,3,4,5
教学案:P3ks5u精品课件ks5u精品课件
试想集合间是否有类似的“大小”关系呢? 温故而知新ks5u精品课件问题1.观察下列各组集合,A与B具有怎样的
关系?如何用数学语言来表达这种关系?
⑴A={-1,1}, B={-1,0,1,2}
⑵A=N,B=R
⑶A={x|x为高一⑶班的男生},
B={y|y为高一⑶班的学生}
⑷A={x|x为江苏人},
B={y|y为中国人}
ks5u精品课件1.集合与集合之间的“包含”关系 如果集合A的任何一个元素都是集合B的元
素,则称集合A是集合B的子集(subset),
记为A?B或B?A,读作:A包含于(is
contained in)集合B”,或“集合B包含
(contains)集合A”.子集的定义ks5u精品课件想一想:如何用Venn图表示两个集合A与B
间的“包含”关系 ?性质:
⑴A?A;
⑵Φ?A;
⑶A?B, B?C则A?Cks5u精品课件想一想:
A?B与B?A能否同时成立?
你能举出一个例子吗? 2.集合与集合之间的 “相等”关系:
若A?B且B?A ,则A=B. ks5u精品课件3.真子集的概念
若集合A?B,存在元素x∈B且x?A,则称集
合A是集合B的真子集(proper subset)。
记作:A B(或BA)读作:A真包含于 B(或B真包含A) 性质:
⑴ A≠Φ,则Φ A;
⑶A B, B C则A Cks5u精品课件例1写出集合{a,b}的所有的子集. 解析:?,{a},{b},{a,b} 变:写出集合{a,b,c}的所有的子集. 解析:?,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}猜想:
若A中有n个元素,A的子集有_____ 个.
若A中有n个元素,A的真子集有_____ 个2n 2n-1 ks5u精品课件练习:1.判断下列说法是否正确: (2)空集是任何集合的真子集; ( × )( × )( × )( × )( × )( √ )ks5u精品课件练习:=ks5u精品课件例2下列三个集合中,哪两个集合具有包含关系?
⑴S={―2,―1,1,2},A={―1,1},B={―2,2};
⑵S=R,A={x|x≤0,x∈R},B={x|x>0,x∈R};
⑶S={x|x为地球人},A={x|x为中国人},
B={x|x为外国人}.思考:观察例2中每一组的三个集合,它们
之间还有一种什么关系? ks5u精品课件 4.补集的概念
补集的定义:设A?S,由S中不属于A的所
有元素组成的集合称为S的子集A的补集
complementary set),简称为集合A的补集,
记作:CsA(读作A在S中的补集)即:
CsA={x|x∈S且x?A}. 5.全集的概念
全集的定义:如果集合S包含我们所要
研究的各个集合这时S可以看着一个全集,
通常记为U.ks5u精品课件想一想:如何用Venn图表示CU A?想一想:CUA在U中的补集等于什么?CU(CUA)=Aks5u精品课件例3 不等式组 的解集为A,U=R,试求A及CUA,并把
它们分别表示在数轴上. 点评:不等式问题通常借助数轴来研究,
但要注意实心点与空心点. ks5u精品课件学生练习:
A组P9练习3,4
ks5u精品课件回顾反思 1.两个集合之间的关系有“包含”、“相等” 、“真包含”、 “不包含” 几种,,同时还要注意区别元素与集合关系及其表示方法.
2.补集的概念必须要有全集的限制.
3.充分利用“形”来解决问题. ks5u精品课件2.预习提纲:
(1)交集与并集的含义是什么?能否说明?
(2)求两个集合交集或并集时如何借助图形.作业1.课后作业:P10习题1,2,3,4,5
教学案:P3ks5u精品课件ks5u精品课件
