资兴市立中学2010年下期高一年级第一次单元测试
文档属性
| 名称 | 资兴市立中学2010年下期高一年级第一次单元测试 |  | |
| 格式 | rar | ||
| 文件大小 | 87.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-29 14:33:00 | ||
图片预览


文档简介
资兴市立中学2010年下期高一年级第一次单元测试
数学试卷
一.选择题(每题5分,共40分)
1.下列六个关系式:① ② ③ ④ ⑤
⑥ 其中正确的个数为( )
A.6个 B.5个 C. 4个 D. 少于4个
2.已知A={(x, y)|x+y=3}, B={(x,y)|x-y=1},则A∩B=( )
A.{2, 1} B.{x=2,y=1} C.{(2,1)} D.(2,1)
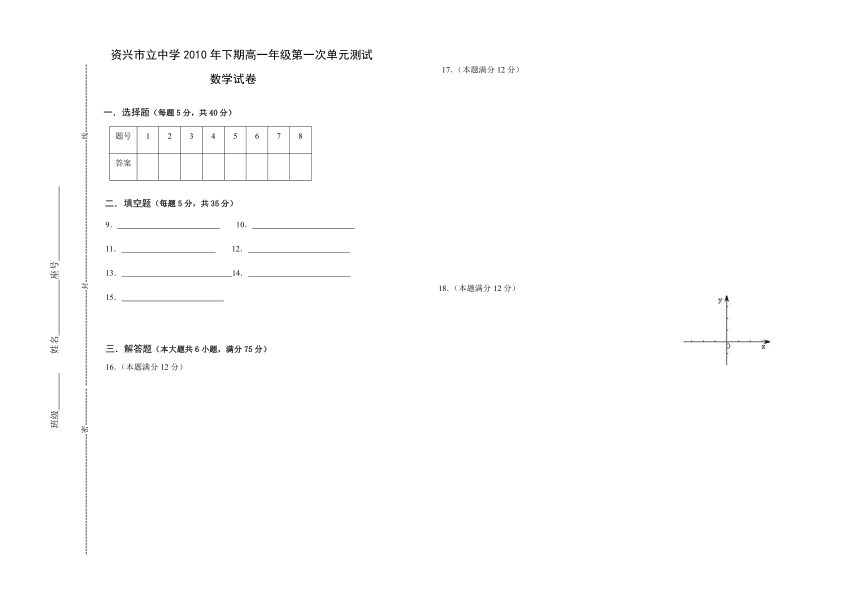
3.如图,U是全集,M.P.S是U的三个子集,则阴影部分所表示的集合是 ( )
A.(M B.(M
C.(MP)(CUS) D.(MP)(CUS)
4.设集合若则的范围是( )
A. B. C. D.
5.下列图象中不能作为函数图象的是( )
6.设集合A和B都是自然数集合N,映射f:A→B把集合A中的元素n映射到集合B中的元素
2n+n,则在映射f下,B中的元素20对应A中的元素是( )
A.2 B.3 C.4 D.5
7.下列各组函数表示同一函数的是┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
A. B.
C. D.
8. 一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示. 某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)
给出以下3个论断:①0点到3点只进水不出水;C②3点到4点不进水只出水;③4点到6点不进水不出水. 则正确论断的个数是( )
A. 3 B. 2 C. 1 D. 0
二.填空题(每题5分,共35分)
9.定义集合A、B的一种运算:,若,
,则中的所有元素数字之和为 .
10.已知函数,则等于 .
11.函数是定义在R上的奇函数,当时,,则当时,
等于 .
12.函数的定义域为 .
13.已知函数 若,则 .
14.已知函数满足对所有的实数都有,则的值为 ..
15.函数在区间上递减,则实数的取值范围是 .
三.解答题(本大题共6小题,满分75分)
16.(本题满分12分)
⑴ 用列举法表示集合;
⑵ 用描述法表示“比大,且比小的所有实数”组成的集合;
⑶ 用另一种方法表示集合.
17.(本题满分12分)
已知函数
⑴ 判断函数的单调性,并证明;
⑵ 求函数的最大值和最小值.
18.(本题满分12分)
已知函数
⑴ 证明:函数是偶函数;
⑵ 利用绝对值及分段函数知识,将函数解析式
写成分段函数,然后画出函数图像;
⑶ 写出函数的值域.
19.(本题满分12分)
某摩托车生产企业,上年度生产摩托车的投入成本为每辆1万元,出厂价为每辆1.2万元,年销售量为1000辆,本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为x (0<x<1),则出厂价相应的提高比例为0.75x,同时预计年销售量增加的比例为0.6x.
已知年利润 = (出厂价 – 投入成本)×年销售量
(1)写出本年度预计的年利润y与投入成本增加的比例x的关系式;
(2)为使本年度的年利润比上年有所增加,问投入成本增加的比例x应在什么范围内?.
20.(本题满分13分)
设是定义在上的函数,对任意,恒有。
⑴求的值;
⑵求证为奇函数;
⑶若函数是上的增函数,已知,求的取值范围。
21.(本题满分14分)
二次函数f (x) = ax2 + bx + c (a,b∈R,a≠0)满足条件:
①当x∈R时,的图象关于直线对称;
② ;
③f (x)在R上的最小值为0;
(1)求函数f (x)的解析式;
(2)求最大的m (m>1),使得存在t∈R,只要x∈[1,m],就有f (x + t)≤x.
资兴市立中学2010年下期高一年级第一次单元测试
数学试卷
一.选择题(每题5分,共40分)
题号
1
2
3
4
5
6
7
8
答案
二.填空题(每题5分,共35分)
9. 10.
11. 12.
13. 14.
15.
三.解答题(本大题共6小题,满分75分)
16.(本题满分12分)
17.(本题满分12分)
18.(本题满分12分)
19.(本题满分12分)
20.(本题满分13分)
21.(本题满分14分)
资兴市立中学2010年下期高一年级第一次单元测试
数学试卷参考答案
一.选择题(每题5分,共40分)
题号
1
2
3
4
5
6
7
8
答案
C
C
C
A
B
C
C
C
二.填空题(每题5分,共35分)
9 . 10 . 11. 12.
13. 14. 15.
三.解答题(本大题共6小题,满分75分)
16.(本题满分12分)
解: ⑴ ⑵
⑶
17.(12分) 解:⑴ 设任取且
5分
即
在上为增函数. 8分
⑵ 由⑴知,在上为增函数,则
12分
18.(12分) 解: ⑴ 由于
是偶函数
⑵ 7分 9分
⑶ 由函数图象知,函数的值域为
19. 【解析】(1)依题意,得y = [1.2×(1 + 0.75x) – 1×(1 + x)] ×1000 (1 + 0.6x)
整理得y = –60x2 + 20x + 200 (0<x<1)
(2)依题意,得
答:(略)
20.(本题满分13分)
解: ⑴令y=x=0得 f(0)=2f(0)→f(0)=0
⑵令y= -x得 f(0)=f(x)+f(-x) →f(-x)= -f(x) 又函数的定义域为为奇函数
⑶∵又f(1)=1 ∴2= f(1)+ f(1)=f(1+1)= f(2)
∴即为
又f(a-1)+f(2)=f(a-1+2)=f(a+1)
∴f(2a)> f(a+1) 又函数是上的增函数
∴2a>a+1得a>1 ∴的取值范围是
21.(本题满分14分)【解析】(1)∵f (x)的对称轴为x = –1,∴= –1即b = 2a.
又f (1) = 1,即a + b + c = 1.
由条件③知:a>0,且= 0,即b2 = 4ac.
由上可求得
∴.
(2)由(1)知:f (x) =(x + 1)2,图象开口向上.
而y = f (x + t )的图象是由y = f (x)平移t个单位得到,要x∈[1,m]时,f (x + t)≤x,
即y = f (x + t)的图象在y = x的图象的下方,且m最大.
∴1,m应该是y = f (x + t)与y = x的交点横坐标,
即1,m是(x + t + 1)2 = x的两根,
由1是(x + t + 1)2 = x的一个根,得(t + 2)2 = 4,解得t = 0,或t = -4,
把t = 0代入原方程得x1 = x2 = 1(这与m>1矛盾)
把t = –4代入原方程得x2 – 10x + 9 = 0,解得x1 = 1,x2 = 9.∴m = 9.
综上知:m的最大值为9.
数学试卷
一.选择题(每题5分,共40分)
1.下列六个关系式:① ② ③ ④ ⑤
⑥ 其中正确的个数为( )
A.6个 B.5个 C. 4个 D. 少于4个
2.已知A={(x, y)|x+y=3}, B={(x,y)|x-y=1},则A∩B=( )
A.{2, 1} B.{x=2,y=1} C.{(2,1)} D.(2,1)
3.如图,U是全集,M.P.S是U的三个子集,则阴影部分所表示的集合是 ( )
A.(M B.(M
C.(MP)(CUS) D.(MP)(CUS)
4.设集合若则的范围是( )
A. B. C. D.
5.下列图象中不能作为函数图象的是( )
6.设集合A和B都是自然数集合N,映射f:A→B把集合A中的元素n映射到集合B中的元素
2n+n,则在映射f下,B中的元素20对应A中的元素是( )
A.2 B.3 C.4 D.5
7.下列各组函数表示同一函数的是┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
A. B.
C. D.
8. 一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示. 某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)
给出以下3个论断:①0点到3点只进水不出水;C②3点到4点不进水只出水;③4点到6点不进水不出水. 则正确论断的个数是( )
A. 3 B. 2 C. 1 D. 0
二.填空题(每题5分,共35分)
9.定义集合A、B的一种运算:,若,
,则中的所有元素数字之和为 .
10.已知函数,则等于 .
11.函数是定义在R上的奇函数,当时,,则当时,
等于 .
12.函数的定义域为 .
13.已知函数 若,则 .
14.已知函数满足对所有的实数都有,则的值为 ..
15.函数在区间上递减,则实数的取值范围是 .
三.解答题(本大题共6小题,满分75分)
16.(本题满分12分)
⑴ 用列举法表示集合;
⑵ 用描述法表示“比大,且比小的所有实数”组成的集合;
⑶ 用另一种方法表示集合.
17.(本题满分12分)
已知函数
⑴ 判断函数的单调性,并证明;
⑵ 求函数的最大值和最小值.
18.(本题满分12分)
已知函数
⑴ 证明:函数是偶函数;
⑵ 利用绝对值及分段函数知识,将函数解析式
写成分段函数,然后画出函数图像;
⑶ 写出函数的值域.
19.(本题满分12分)
某摩托车生产企业,上年度生产摩托车的投入成本为每辆1万元,出厂价为每辆1.2万元,年销售量为1000辆,本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为x (0<x<1),则出厂价相应的提高比例为0.75x,同时预计年销售量增加的比例为0.6x.
已知年利润 = (出厂价 – 投入成本)×年销售量
(1)写出本年度预计的年利润y与投入成本增加的比例x的关系式;
(2)为使本年度的年利润比上年有所增加,问投入成本增加的比例x应在什么范围内?.
20.(本题满分13分)
设是定义在上的函数,对任意,恒有。
⑴求的值;
⑵求证为奇函数;
⑶若函数是上的增函数,已知,求的取值范围。
21.(本题满分14分)
二次函数f (x) = ax2 + bx + c (a,b∈R,a≠0)满足条件:
①当x∈R时,的图象关于直线对称;
② ;
③f (x)在R上的最小值为0;
(1)求函数f (x)的解析式;
(2)求最大的m (m>1),使得存在t∈R,只要x∈[1,m],就有f (x + t)≤x.
资兴市立中学2010年下期高一年级第一次单元测试
数学试卷
一.选择题(每题5分,共40分)
题号
1
2
3
4
5
6
7
8
答案
二.填空题(每题5分,共35分)
9. 10.
11. 12.
13. 14.
15.
三.解答题(本大题共6小题,满分75分)
16.(本题满分12分)
17.(本题满分12分)
18.(本题满分12分)
19.(本题满分12分)
20.(本题满分13分)
21.(本题满分14分)
资兴市立中学2010年下期高一年级第一次单元测试
数学试卷参考答案
一.选择题(每题5分,共40分)
题号
1
2
3
4
5
6
7
8
答案
C
C
C
A
B
C
C
C
二.填空题(每题5分,共35分)
9 . 10 . 11. 12.
13. 14. 15.
三.解答题(本大题共6小题,满分75分)
16.(本题满分12分)
解: ⑴ ⑵
⑶
17.(12分) 解:⑴ 设任取且
5分
即
在上为增函数. 8分
⑵ 由⑴知,在上为增函数,则
12分
18.(12分) 解: ⑴ 由于
是偶函数
⑵ 7分 9分
⑶ 由函数图象知,函数的值域为
19. 【解析】(1)依题意,得y = [1.2×(1 + 0.75x) – 1×(1 + x)] ×1000 (1 + 0.6x)
整理得y = –60x2 + 20x + 200 (0<x<1)
(2)依题意,得
答:(略)
20.(本题满分13分)
解: ⑴令y=x=0得 f(0)=2f(0)→f(0)=0
⑵令y= -x得 f(0)=f(x)+f(-x) →f(-x)= -f(x) 又函数的定义域为为奇函数
⑶∵又f(1)=1 ∴2= f(1)+ f(1)=f(1+1)= f(2)
∴即为
又f(a-1)+f(2)=f(a-1+2)=f(a+1)
∴f(2a)> f(a+1) 又函数是上的增函数
∴2a>a+1得a>1 ∴的取值范围是
21.(本题满分14分)【解析】(1)∵f (x)的对称轴为x = –1,∴= –1即b = 2a.
又f (1) = 1,即a + b + c = 1.
由条件③知:a>0,且= 0,即b2 = 4ac.
由上可求得
∴.
(2)由(1)知:f (x) =(x + 1)2,图象开口向上.
而y = f (x + t )的图象是由y = f (x)平移t个单位得到,要x∈[1,m]时,f (x + t)≤x,
即y = f (x + t)的图象在y = x的图象的下方,且m最大.
∴1,m应该是y = f (x + t)与y = x的交点横坐标,
即1,m是(x + t + 1)2 = x的两根,
由1是(x + t + 1)2 = x的一个根,得(t + 2)2 = 4,解得t = 0,或t = -4,
把t = 0代入原方程得x1 = x2 = 1(这与m>1矛盾)
把t = –4代入原方程得x2 – 10x + 9 = 0,解得x1 = 1,x2 = 9.∴m = 9.
综上知:m的最大值为9.
