高二数学:空间向量及其加减与数乘运算
文档属性
| 名称 | 高二数学:空间向量及其加减与数乘运算 |

|
|
| 格式 | rar | ||
| 文件大小 | 228.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-30 00:00:00 | ||
图片预览





文档简介
课件32张PPT。空间向量及其加减与数乘运算一、平面向量复习⒈定义:既有大小又有方向的量叫向量. 几何表示法:用有向线段表示; 字母表示法:用字母a、b等或者用有向线段
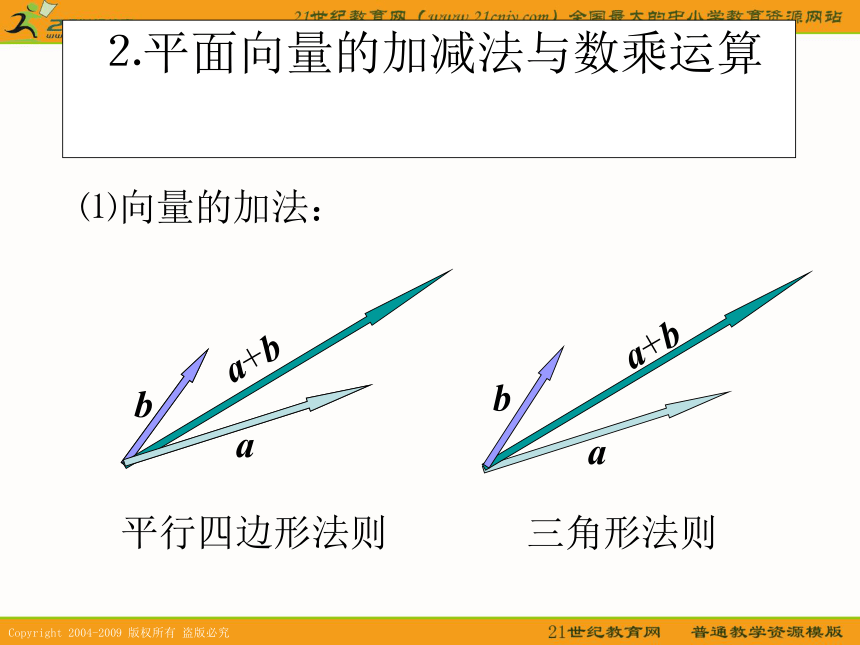
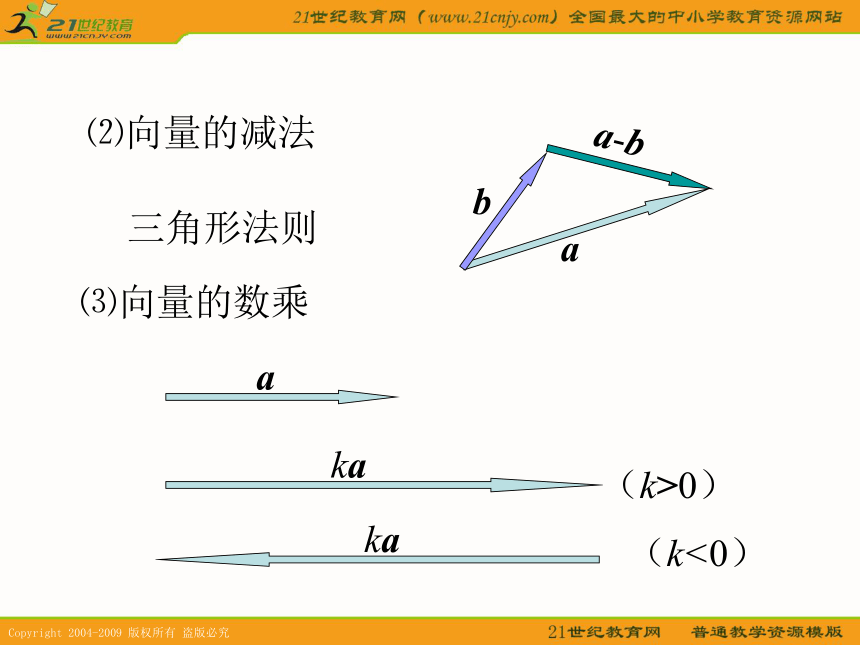
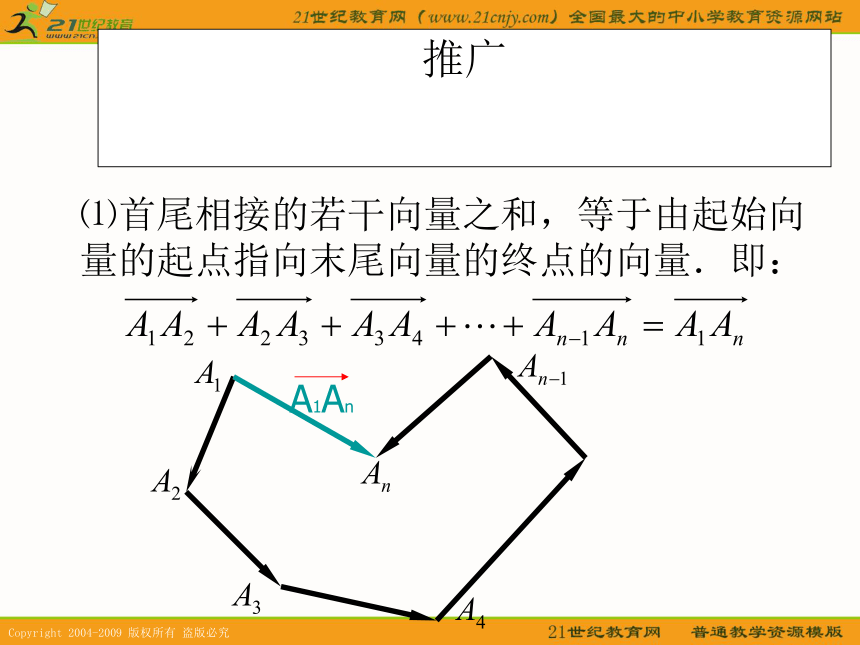
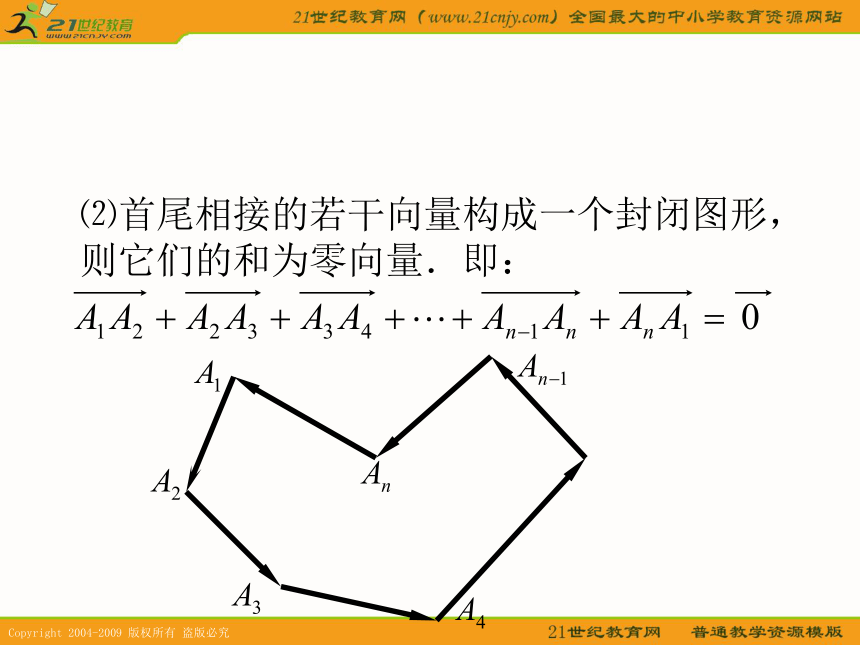
的起点与终点字母 表示.相等的向量: 长度相等且方向相同的向量. ⒉平面向量的加减法与数乘运算⑴向量的加法:aba+b平行四边形法则aa+b三角形法则⑵向量的减法aba-b三角形法则⑶向量的数乘aka(k>0)ka(k<0)⒊平面向量的加法与数乘运算律加法交换律:a+b=b+a 加法结合律:(a+b)+c=a+(b+c) 数乘分配律:λ(a+b)=λa+λb 推广⑴首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:⑵首尾相接的若干向量构成一个封闭图形,则它们的和为零向量.即:二、空间向量及其加减与数乘运算⒈空间向量:空间中具有大小和方向的量叫做向量.⑴定义:⑵表示方法:①空间向量的表示方法和平面向量一样;③空间任意两个向量都可以用同一平面
内的两条有向线段表示.②同向且等长的有向线段表示同一向量或
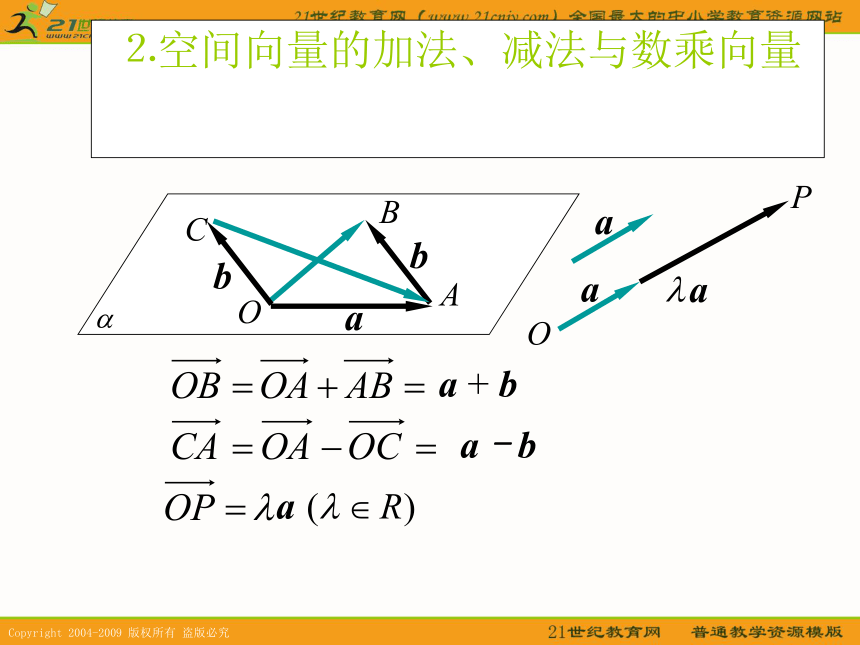
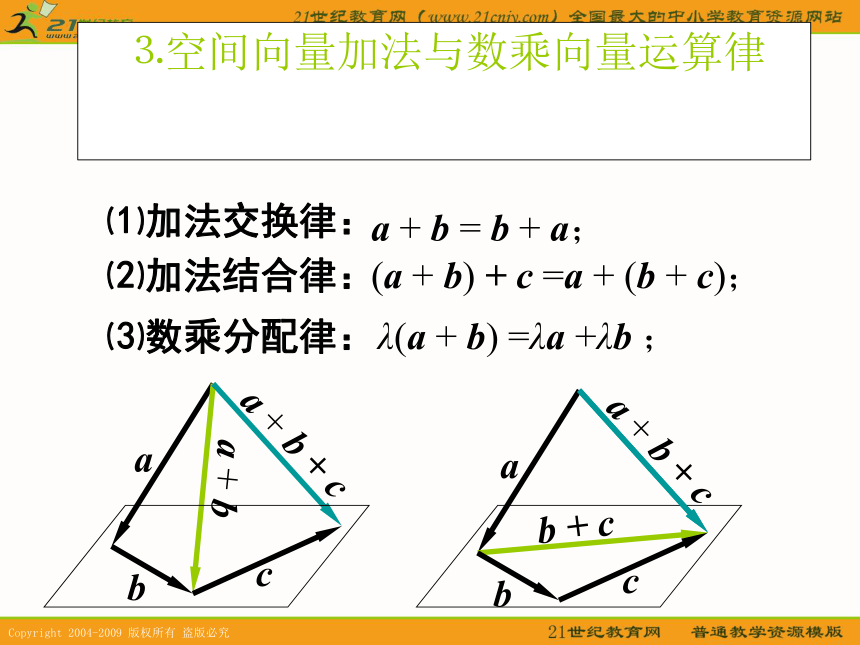
相等的向量;⒉空间向量的加法、减法与数乘向量a + baaOPa - b⒊空间向量加法与数乘向量运算律⑴加法交换律:a + b = b + a;⑵加法结合律:(a + b) + c =a + (b + c);⑶数乘分配律:λ(a + b) =λa +λb ;abca + b + c abca + b + c a + b b + c 对空间向量的加法、减法与数乘向量的说明⒈空间向量的运算就是平面向量运算的推广.⒉两个向量相加的平行四边形法则在空间仍
然成立.⒊空间向量的加法运算可以推广至若干个向
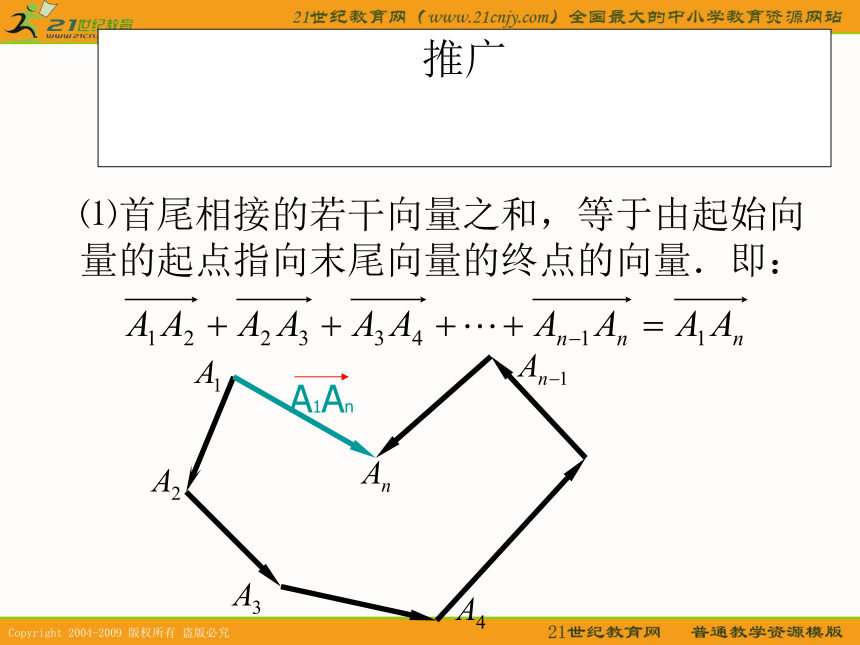
量相加.推广⑴首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:⑵首尾相接的若干向量构成一个封闭图形,则它们的和为零向量.即:例1解:始点相同的三个不共面向量之和,等于以这三个向量
为棱的平行六面体的以公共始点为始点的对角线所示向量⑶设M是线段CC’的中点,则解:⑷设G是线段AC’靠近点A的
三等分点,则G解:例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。解:例2:已知平行六面体
ABCD-A1B1C1D1,
求满足下列各式的x的值。解:ABMCGD练习一:空间四边形ABCD中,M、G分别
是BC、CD边的中点,化简:(27面练习第1题
(2)、(3)问。ABMCGD(2)原式练习一:空间四边形ABCD中,M、G分别是BC、CD边
的中点,化简:练习二:在正方体ABCD-A’B’C’D’中,点E是面
AC’的中心,求下列各式中的x、y的值.练习二:在正方体ABCD-A’B’C’D’中,点E是面
AC’的中心,求下列各式中的x、y的值.练习二:在正方体ABCD-A’B’C’D’中,点E是面
AC’的中心,求下列各式中的x、y的值.平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律小结类比、数形结合数乘:ka,k为正数,负数,零作业:课本P27 练习 ⒈ ⒉aABCDA’B’C’D’例:空间一个平移就是一个向量.一、平面向量复习⒈定义:既有大小又有方向的量叫向量 几何表示法:用有向线段表示; 字母表示法:用字母a、b等或者用有向线段
的起点与终点字母 表示.相等的向量: 长度相等且方向相同的向量 平行六面体 平行四边形ABCD平移向量 a 到A’B’C’D’的轨迹所形成的几何体,叫做平行六面体.记作ABCD—A’B’C’D’.A’B’C’D’ 平行六面体的六个面都是平行四边形,每个面的边叫做平行六面体的棱.
的起点与终点字母 表示.相等的向量: 长度相等且方向相同的向量. ⒉平面向量的加减法与数乘运算⑴向量的加法:aba+b平行四边形法则aa+b三角形法则⑵向量的减法aba-b三角形法则⑶向量的数乘aka(k>0)ka(k<0)⒊平面向量的加法与数乘运算律加法交换律:a+b=b+a 加法结合律:(a+b)+c=a+(b+c) 数乘分配律:λ(a+b)=λa+λb 推广⑴首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:⑵首尾相接的若干向量构成一个封闭图形,则它们的和为零向量.即:二、空间向量及其加减与数乘运算⒈空间向量:空间中具有大小和方向的量叫做向量.⑴定义:⑵表示方法:①空间向量的表示方法和平面向量一样;③空间任意两个向量都可以用同一平面
内的两条有向线段表示.②同向且等长的有向线段表示同一向量或
相等的向量;⒉空间向量的加法、减法与数乘向量a + baaOPa - b⒊空间向量加法与数乘向量运算律⑴加法交换律:a + b = b + a;⑵加法结合律:(a + b) + c =a + (b + c);⑶数乘分配律:λ(a + b) =λa +λb ;abca + b + c abca + b + c a + b b + c 对空间向量的加法、减法与数乘向量的说明⒈空间向量的运算就是平面向量运算的推广.⒉两个向量相加的平行四边形法则在空间仍
然成立.⒊空间向量的加法运算可以推广至若干个向
量相加.推广⑴首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:⑵首尾相接的若干向量构成一个封闭图形,则它们的和为零向量.即:例1解:始点相同的三个不共面向量之和,等于以这三个向量
为棱的平行六面体的以公共始点为始点的对角线所示向量⑶设M是线段CC’的中点,则解:⑷设G是线段AC’靠近点A的
三等分点,则G解:例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例2:已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。解:例2:已知平行六面体
ABCD-A1B1C1D1,
求满足下列各式的x的值。解:ABMCGD练习一:空间四边形ABCD中,M、G分别
是BC、CD边的中点,化简:(27面练习第1题
(2)、(3)问。ABMCGD(2)原式练习一:空间四边形ABCD中,M、G分别是BC、CD边
的中点,化简:练习二:在正方体ABCD-A’B’C’D’中,点E是面
AC’的中心,求下列各式中的x、y的值.练习二:在正方体ABCD-A’B’C’D’中,点E是面
AC’的中心,求下列各式中的x、y的值.练习二:在正方体ABCD-A’B’C’D’中,点E是面
AC’的中心,求下列各式中的x、y的值.平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律小结类比、数形结合数乘:ka,k为正数,负数,零作业:课本P27 练习 ⒈ ⒉aABCDA’B’C’D’例:空间一个平移就是一个向量.一、平面向量复习⒈定义:既有大小又有方向的量叫向量 几何表示法:用有向线段表示; 字母表示法:用字母a、b等或者用有向线段
的起点与终点字母 表示.相等的向量: 长度相等且方向相同的向量 平行六面体 平行四边形ABCD平移向量 a 到A’B’C’D’的轨迹所形成的几何体,叫做平行六面体.记作ABCD—A’B’C’D’.A’B’C’D’ 平行六面体的六个面都是平行四边形,每个面的边叫做平行六面体的棱.
