12.3.1等腰三角形的性质
文档属性
| 名称 | 12.3.1等腰三角形的性质 |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-04 08:47:00 | ||
图片预览

文档简介
课件25张PPT。南门学校 八年(3。5)班给我最大快乐的,不是已懂的知识,
而是不断的学习.----高斯12.3.1等腰三角形的性质 等腰三角形的相关概念
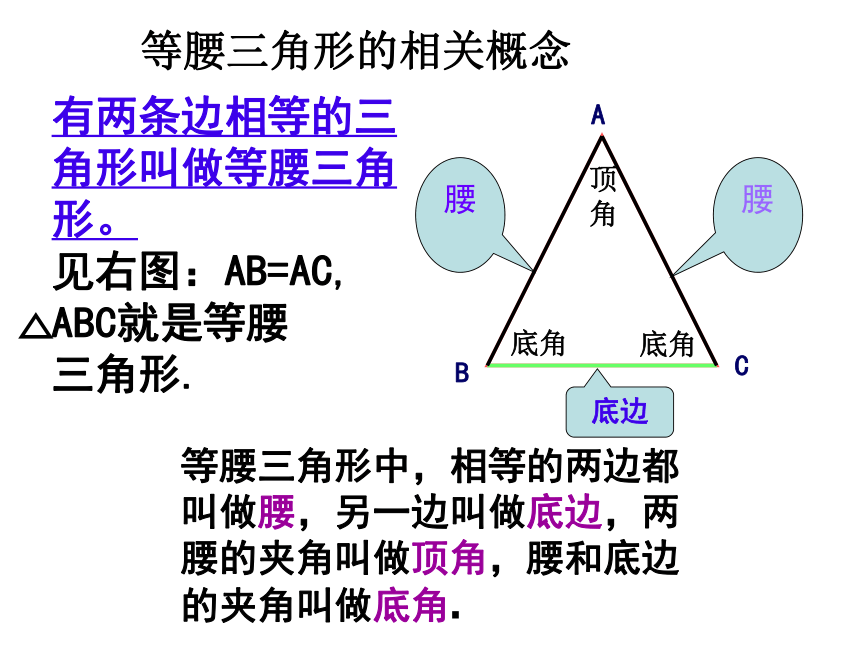
底边等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.有两条边相等的三角形叫做等腰三角形。
见右图:AB=AC, ABC就是等腰
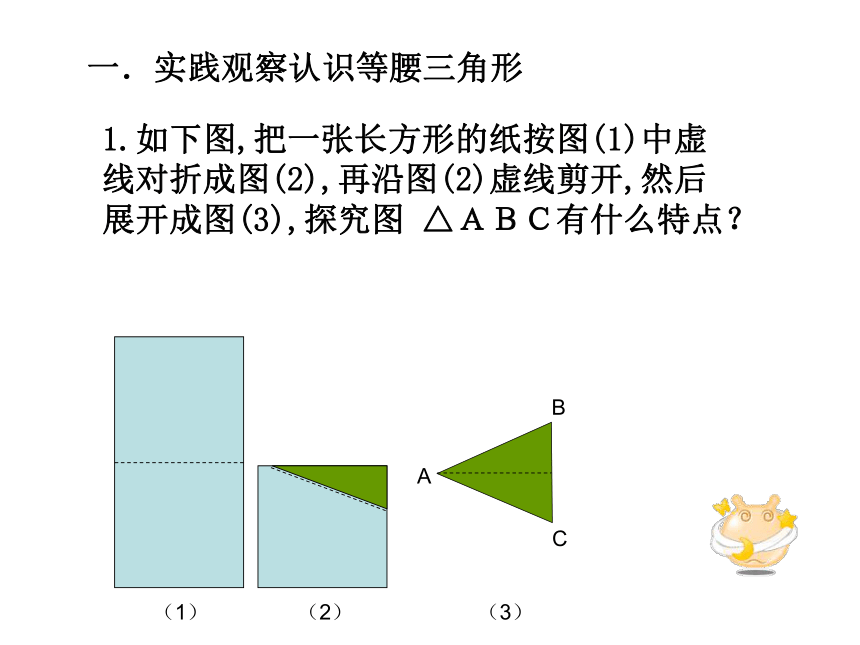
三角形.一.实践观察认识等腰三角形1.如下图,把一张长方形的纸按图(1)中虚线对折成图(2),再沿图(2)虚线剪开,然后展开成图(3),探究图 △ABC有什么特点?ABC (1) (2) (3)发现1:等腰三角形是一个
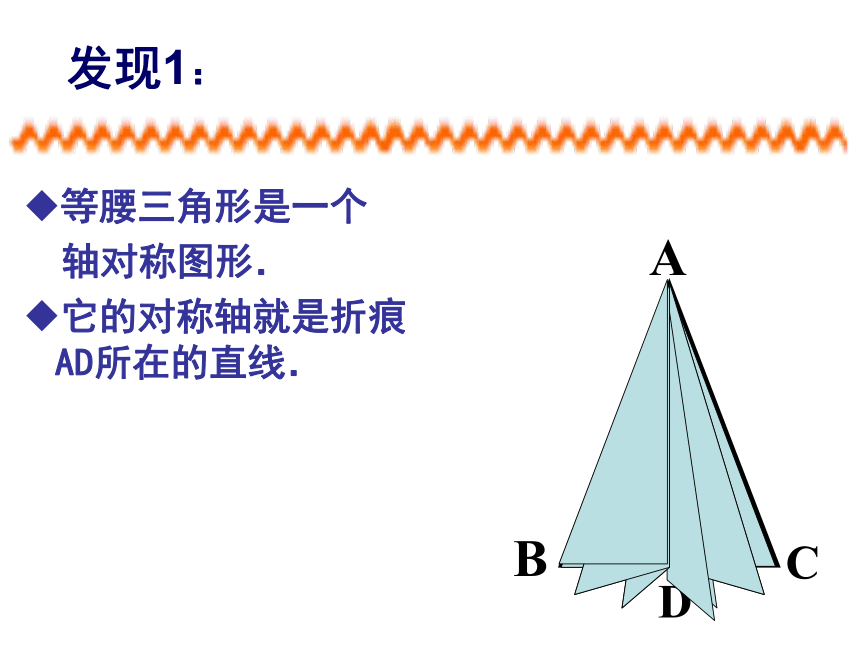
轴对称图形.
它的对称轴就是折痕AD所在的直线.
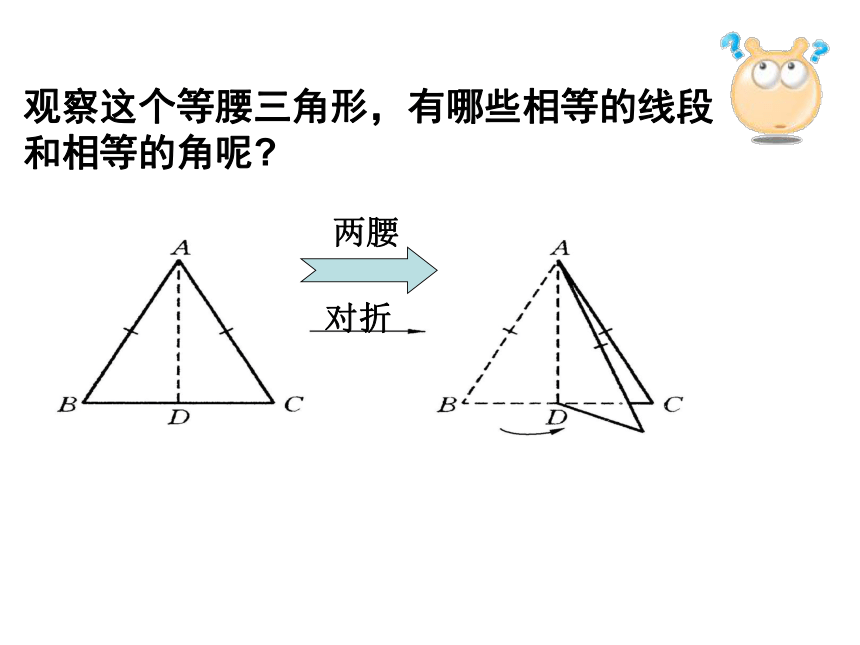
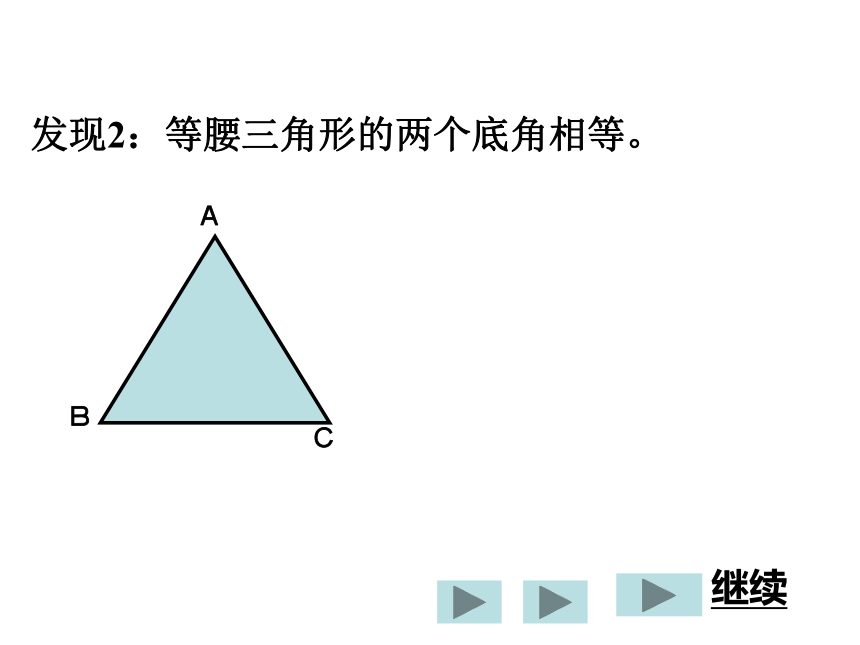
观察这个等腰三角形,有哪些相等的线段 和相等的角呢?继续发现2:等腰三角形的两个底角相等。已知: ΔABC中,AB=AC 求证:∠B=∠C
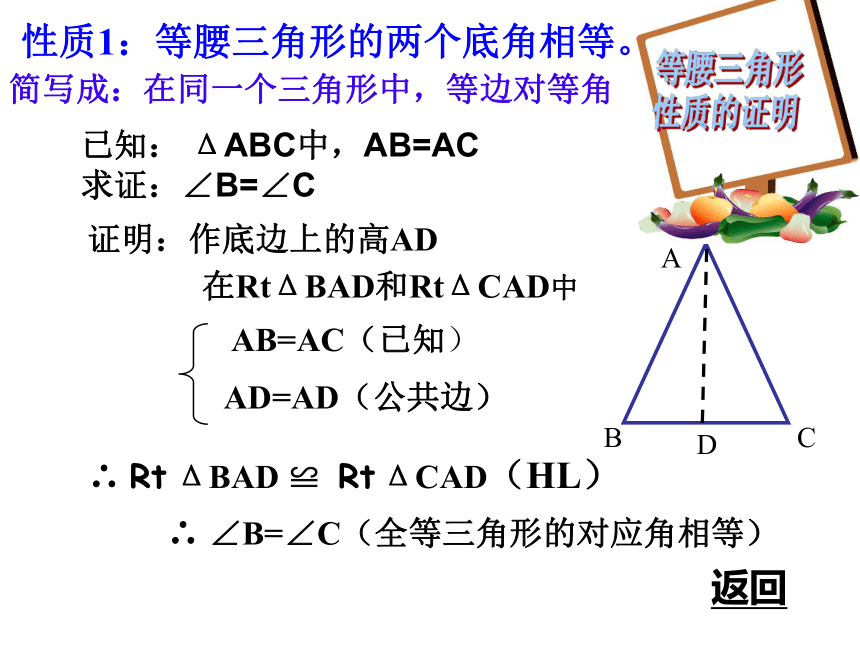
证明:作底边上的高AD 在RtΔBAD和RtΔCAD中AB=AC(已知)AD=AD(公共边)∴ Rt ΔBAD ≌ Rt ΔCAD(HL)∴ ∠B=∠C(全等三角形的对应角相等)性质1:等腰三角形的两个底角相等。简写成:在同一个三角形中,等边对等角等腰三角形
性质的证明返回已知: ΔABC中,AB=AC 求证:∠B=∠C
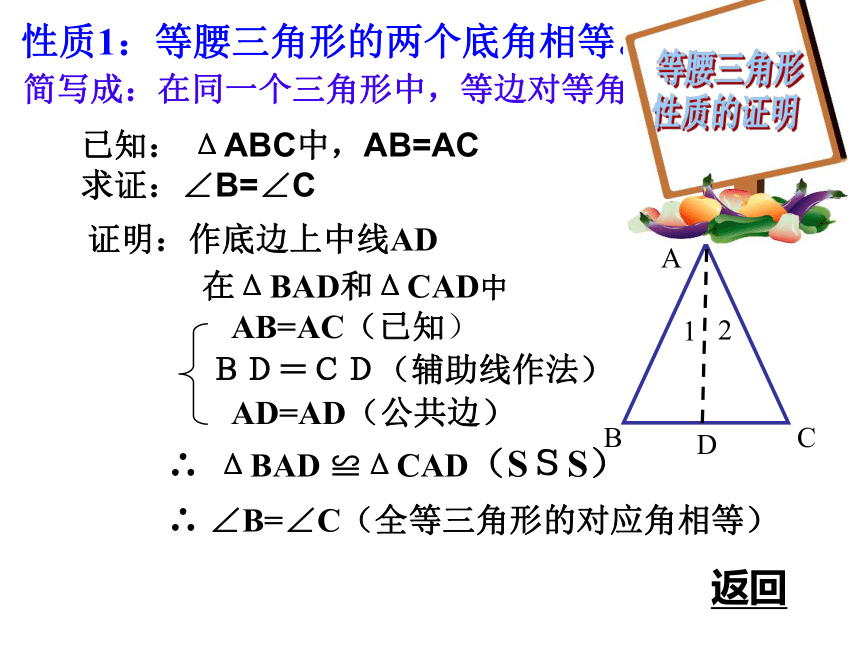
证明:作底边上中线AD 在ΔBAD和ΔCAD中AB=AC(已知)BD=CD(辅助线作法)AD=AD(公共边)∴ ΔBAD ≌ΔCAD(SSS)∴ ∠B=∠C(全等三角形的对应角相等)性质1:等腰三角形的两个底角相等。简写成:在同一个三角形中,等边对等角等腰三角形
性质的证明返回已知: ΔABC中,AB=AC 求证:∠B=∠C
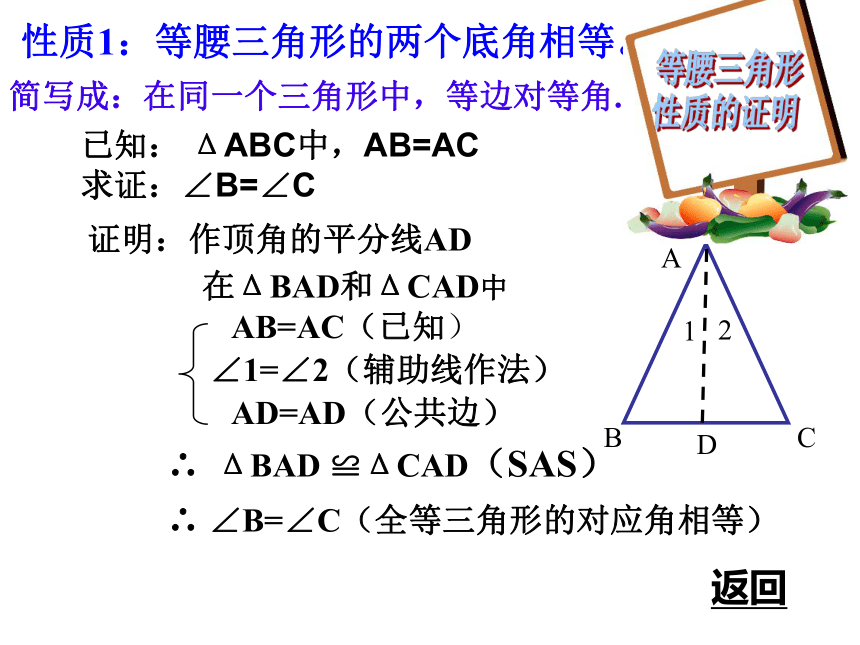
证明:作顶角的平分线AD 在ΔBAD和ΔCAD中AB=AC(已知)∠1=∠2(辅助线作法)AD=AD(公共边)∴ ΔBAD ≌ΔCAD(SAS)∴ ∠B=∠C(全等三角形的对应角相等)性质1:等腰三角形的两个底角相等。等腰三角形
性质的证明简写成:在同一个三角形中,等边对等角.返回性质1: 等腰三角形的两个底角相等.
简写成:在同一个三角形中,等边对等角.符号语言:在△ABC中
∵ AC=AB(已知)
∴ ∠B=∠C
(在同一个三角形中,等边对等角)
第三个发现:∠ADB=∠ADC=90°
AD为底边上的高
BD=CD,
AD为底边上的中线
∠BAD=∠CAD,
AD为顶角的平分线
等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合,简称“三线合一”性质2:等腰三角形的顶角平分线、
底边上的中线和底边上的高
互相重合,简称“三线合一”
12在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。 等腰三角形“三线合一”的性质用符号语言表示为:12BDCD12ADBCADBCBDCD例1、已知:如图,在△ABC中,AB = AC,
∠A = 50°.
求: ∠B 和 ∠C的度数。ABC变式:
已知:等腰三角形的一个内角为 50 °
求: 另两个角的度数.设∠A=x则∠2 =x,
∴∠1=∠A+∠2=2x
∴∠ABC=∠C=∠1=2x
∵∠A+∠ABC+∠C=180°
∴x+2x+2x=180°解得x=36°
∴在△ABC中,∠A=36°,
∠ABC=∠C=72°
解:在△ABC中,
∵AB=AC, BD=BC=AD
∴∠ABC=∠C=∠1
∠A=∠2(在同一个三角形中,等边对等角)例2 如图:在△ABC中,AB=AC,点D在AC上,
且BC=AD=BD,求△ABC各角的度数。12练习判断下列语句是否正确。(1)等腰三角形的角平分线、中线和高互相重合。( )
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°. ( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××作业 75°, 30°35°,35°2. 已知等腰三角形的一个角等于36°,那么它的
另外两个角的度数分别是 ;3.等腰三角形一个角为110°,它的另外两个角
为______1.等腰三角形一个底角为75°,它的另外两个角为_______
36°, 108°或72°, 72°6. 已知等腰三角形的一边长等于5,另一边长等于9,
那么它的周长等于 ;19 或 234. 已知等腰三角形的一个外角等于100°, 那么
它的顶角的度数是 ;80°或20°5. 已知等腰三角形一角是另一角的2倍,则各内角
的度数分别是 ;45°, 45°, 90°,或72°, 72°, 36°7. 已知等腰三角形的一边长等于3,另一边长等于6,
那么它的周长等于 ;15例2、已知:在△ABC中,E是CA延长
上的点,且AB = AC ,
AE = AD。请说明:1)∠BAC=2∠ E。
2)ED⊥BCABCD提高练习:E文字叙述几何语言等腰三角形的两底角相等(简称在同一个三角形中,等边对等角)∵AB=AC
∴∠B=∠C等腰三角形顶角的平分线平分底边并且垂直于底边(简称三线合一)∵AB=AC,∠1=∠2 ∴AD⊥BC,BD=CD课堂小结在△ABC中,在△ABC中,4、巩固提高 (2).如图,AOB是一钢架,且∠AOB=10°,为使钢架更加坚固,需在其内部添一些钢管EF、FG、GH……,添加的钢管长度都与OE相等,则最多能添加这样的钢管 根。EGOFHMBA趣味数学:如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,求∠ MEF的度数。10. 如图, AB=AE,∠ABC=∠AED,BC=ED,点F是CD的
中点.
(1)判断AF与CD的位置关系?为什么?ABCDEF(2)连接BE后,又能得出什么新的结论?不妨说出几个!等腰三角形三线合一性质是怎么叙述的?等腰三角形的顶角平分线、底边上的中线、底边上的高线相互重合.1.等腰三角形的顶角平分线也是底边上的中线、底边上的高线.2.等腰三角形底边上的中线也是的顶角平分线、 底边上的高线.3.等腰三角形的底边上的高线也是顶角平分线、底边上的中线.还记得吗∠BAD=∠CADBD=CDAD⊥BCBD=CD∠BAD=∠CADAD⊥BCAD⊥BC∠BAD=∠CADBD=CD寄语 如果你智慧的双眼善于观察,善于发现,那你一定会觉得数学就在我们的身边。
老师相信:你辛勤的汗水一定会浇灌出智慧的花朵!
而是不断的学习.----高斯12.3.1等腰三角形的性质 等腰三角形的相关概念
底边等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.有两条边相等的三角形叫做等腰三角形。
见右图:AB=AC, ABC就是等腰
三角形.一.实践观察认识等腰三角形1.如下图,把一张长方形的纸按图(1)中虚线对折成图(2),再沿图(2)虚线剪开,然后展开成图(3),探究图 △ABC有什么特点?ABC (1) (2) (3)发现1:等腰三角形是一个
轴对称图形.
它的对称轴就是折痕AD所在的直线.
观察这个等腰三角形,有哪些相等的线段 和相等的角呢?继续发现2:等腰三角形的两个底角相等。已知: ΔABC中,AB=AC 求证:∠B=∠C
证明:作底边上的高AD 在RtΔBAD和RtΔCAD中AB=AC(已知)AD=AD(公共边)∴ Rt ΔBAD ≌ Rt ΔCAD(HL)∴ ∠B=∠C(全等三角形的对应角相等)性质1:等腰三角形的两个底角相等。简写成:在同一个三角形中,等边对等角等腰三角形
性质的证明返回已知: ΔABC中,AB=AC 求证:∠B=∠C
证明:作底边上中线AD 在ΔBAD和ΔCAD中AB=AC(已知)BD=CD(辅助线作法)AD=AD(公共边)∴ ΔBAD ≌ΔCAD(SSS)∴ ∠B=∠C(全等三角形的对应角相等)性质1:等腰三角形的两个底角相等。简写成:在同一个三角形中,等边对等角等腰三角形
性质的证明返回已知: ΔABC中,AB=AC 求证:∠B=∠C
证明:作顶角的平分线AD 在ΔBAD和ΔCAD中AB=AC(已知)∠1=∠2(辅助线作法)AD=AD(公共边)∴ ΔBAD ≌ΔCAD(SAS)∴ ∠B=∠C(全等三角形的对应角相等)性质1:等腰三角形的两个底角相等。等腰三角形
性质的证明简写成:在同一个三角形中,等边对等角.返回性质1: 等腰三角形的两个底角相等.
简写成:在同一个三角形中,等边对等角.符号语言:在△ABC中
∵ AC=AB(已知)
∴ ∠B=∠C
(在同一个三角形中,等边对等角)
第三个发现:∠ADB=∠ADC=90°
AD为底边上的高
BD=CD,
AD为底边上的中线
∠BAD=∠CAD,
AD为顶角的平分线
等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合,简称“三线合一”性质2:等腰三角形的顶角平分线、
底边上的中线和底边上的高
互相重合,简称“三线合一”
12在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。 等腰三角形“三线合一”的性质用符号语言表示为:12BDCD12ADBCADBCBDCD例1、已知:如图,在△ABC中,AB = AC,
∠A = 50°.
求: ∠B 和 ∠C的度数。ABC变式:
已知:等腰三角形的一个内角为 50 °
求: 另两个角的度数.设∠A=x则∠2 =x,
∴∠1=∠A+∠2=2x
∴∠ABC=∠C=∠1=2x
∵∠A+∠ABC+∠C=180°
∴x+2x+2x=180°解得x=36°
∴在△ABC中,∠A=36°,
∠ABC=∠C=72°
解:在△ABC中,
∵AB=AC, BD=BC=AD
∴∠ABC=∠C=∠1
∠A=∠2(在同一个三角形中,等边对等角)例2 如图:在△ABC中,AB=AC,点D在AC上,
且BC=AD=BD,求△ABC各角的度数。12练习判断下列语句是否正确。(1)等腰三角形的角平分线、中线和高互相重合。( )
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°. ( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××作业 75°, 30°35°,35°2. 已知等腰三角形的一个角等于36°,那么它的
另外两个角的度数分别是 ;3.等腰三角形一个角为110°,它的另外两个角
为______1.等腰三角形一个底角为75°,它的另外两个角为_______
36°, 108°或72°, 72°6. 已知等腰三角形的一边长等于5,另一边长等于9,
那么它的周长等于 ;19 或 234. 已知等腰三角形的一个外角等于100°, 那么
它的顶角的度数是 ;80°或20°5. 已知等腰三角形一角是另一角的2倍,则各内角
的度数分别是 ;45°, 45°, 90°,或72°, 72°, 36°7. 已知等腰三角形的一边长等于3,另一边长等于6,
那么它的周长等于 ;15例2、已知:在△ABC中,E是CA延长
上的点,且AB = AC ,
AE = AD。请说明:1)∠BAC=2∠ E。
2)ED⊥BCABCD提高练习:E文字叙述几何语言等腰三角形的两底角相等(简称在同一个三角形中,等边对等角)∵AB=AC
∴∠B=∠C等腰三角形顶角的平分线平分底边并且垂直于底边(简称三线合一)∵AB=AC,∠1=∠2 ∴AD⊥BC,BD=CD课堂小结在△ABC中,在△ABC中,4、巩固提高 (2).如图,AOB是一钢架,且∠AOB=10°,为使钢架更加坚固,需在其内部添一些钢管EF、FG、GH……,添加的钢管长度都与OE相等,则最多能添加这样的钢管 根。EGOFHMBA趣味数学:如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,求∠ MEF的度数。10. 如图, AB=AE,∠ABC=∠AED,BC=ED,点F是CD的
中点.
(1)判断AF与CD的位置关系?为什么?ABCDEF(2)连接BE后,又能得出什么新的结论?不妨说出几个!等腰三角形三线合一性质是怎么叙述的?等腰三角形的顶角平分线、底边上的中线、底边上的高线相互重合.1.等腰三角形的顶角平分线也是底边上的中线、底边上的高线.2.等腰三角形底边上的中线也是的顶角平分线、 底边上的高线.3.等腰三角形的底边上的高线也是顶角平分线、底边上的中线.还记得吗∠BAD=∠CADBD=CDAD⊥BCBD=CD∠BAD=∠CADAD⊥BCAD⊥BC∠BAD=∠CADBD=CD寄语 如果你智慧的双眼善于观察,善于发现,那你一定会觉得数学就在我们的身边。
老师相信:你辛勤的汗水一定会浇灌出智慧的花朵!
