12.3.2等腰三角形的复习
文档属性
| 名称 | 12.3.2等腰三角形的复习 |  | |
| 格式 | rar | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-04 08:56:00 | ||
图片预览




文档简介
课件32张PPT。南门学校 八年(3。5)班给我最大快乐的,不是已懂的知识,
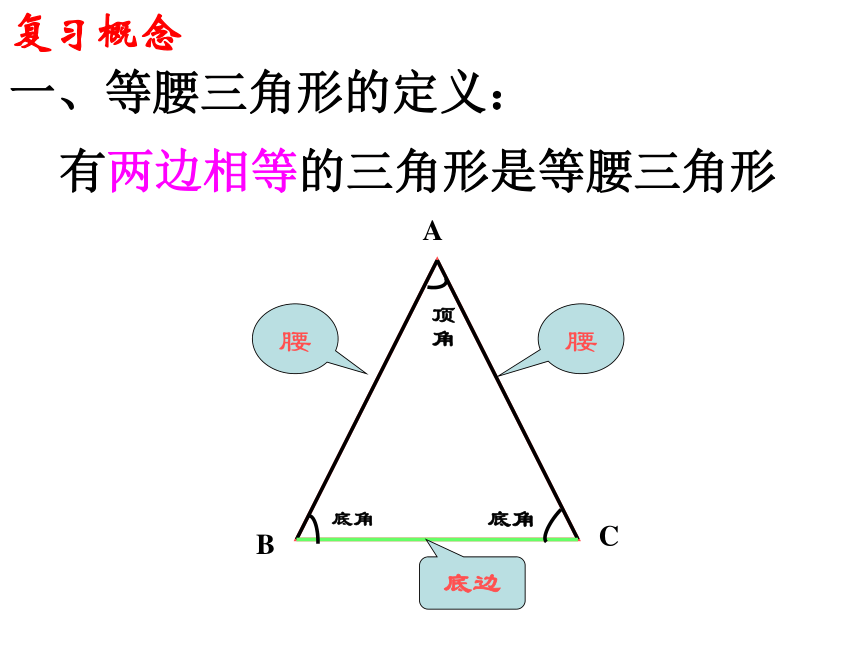
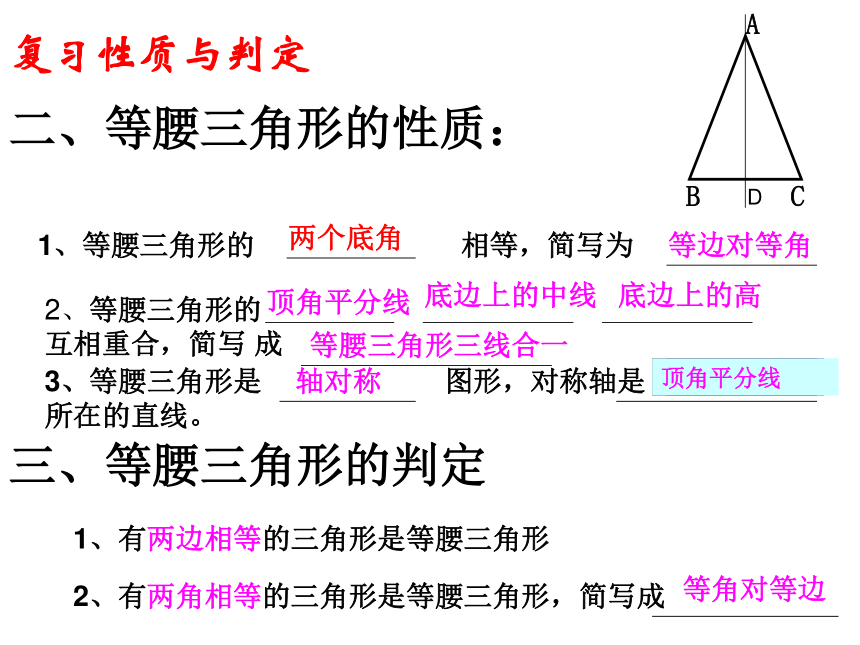
而是不断的学习.----高斯12.3.1等腰三角形的复习复习概念一、等腰三角形的定义:有两边相等的三角形是等腰三角形二、等腰三角形的性质:1、等腰三角形的 相等,简写为2、等腰三角形的 互相重合,简写 成两个底角等边对等角顶角平分线底边上的中线底边上的高等腰三角形三线合一3、等腰三角形是 图形,对称轴是 所在的直线。轴对称三、等腰三角形的判定1、有两边相等的三角形是等腰三角形 2、有两角相等的三角形是等腰三角形,简写成等角对等边顶角平分线底边上的高D底边上的中线顶角平分线复习性质与判定数学学习中,最主要的就是思维方法的培养,只埋头做题,不注意总结反思,成绩是不会有很大提高的,做题不是莽撞的思考,而是有一定规律的。希望每一个同学都做一个学习上的有心人。等腰三角形部分用了哪些数学思想呢?基础知识点的理解与熟记+大量的做题+不断的总结
=数学高手数学思想5、等腰三角形有 条对称轴。1、等腰三角形有两边长分别为3cm、4cm,则周长
为 cm。2、等腰三角形有两边长分别为2cm、4cm,则周长
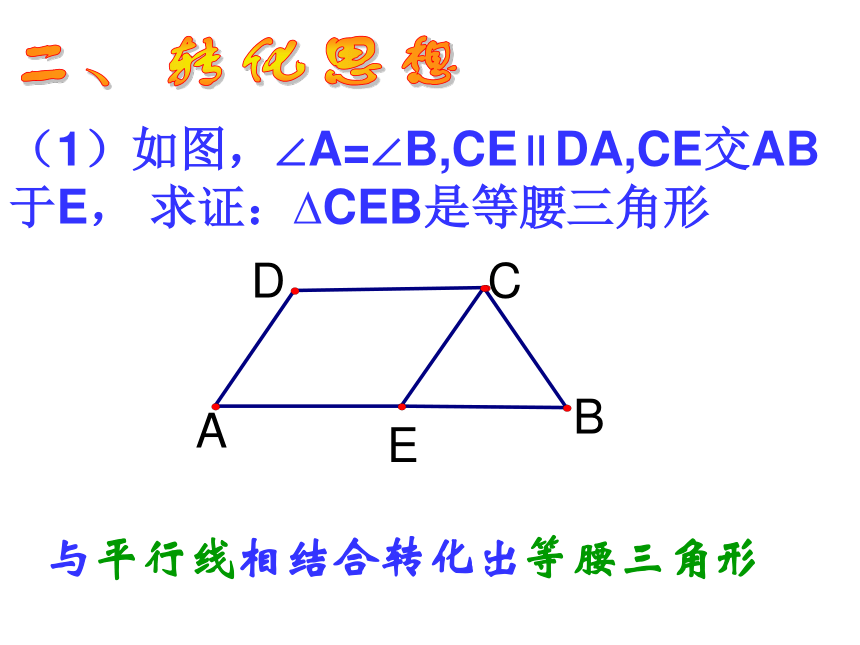
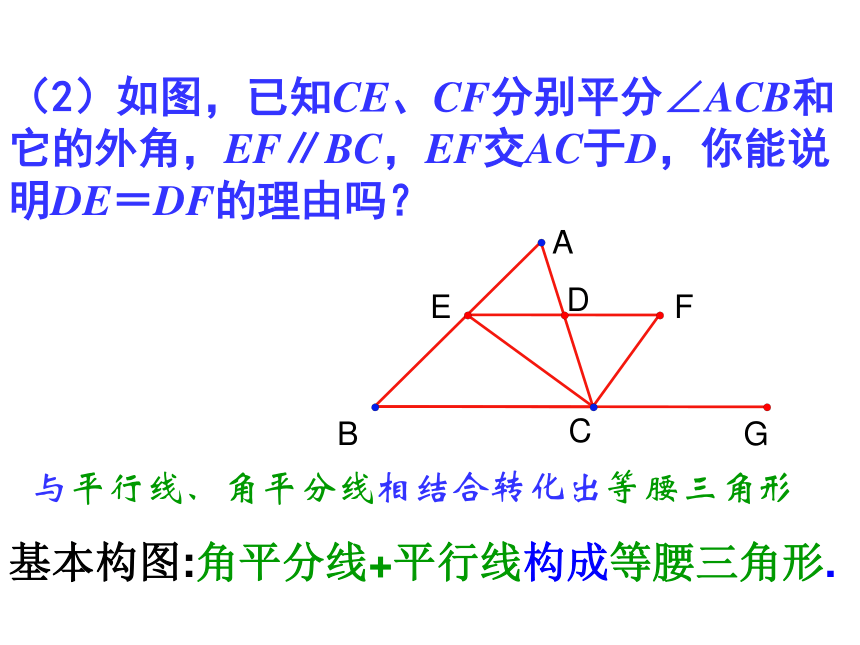
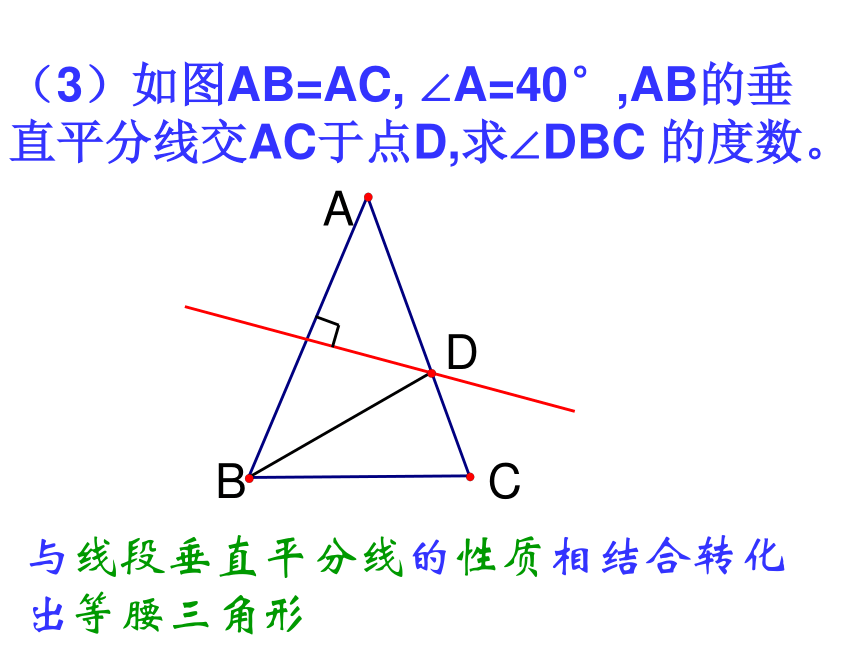
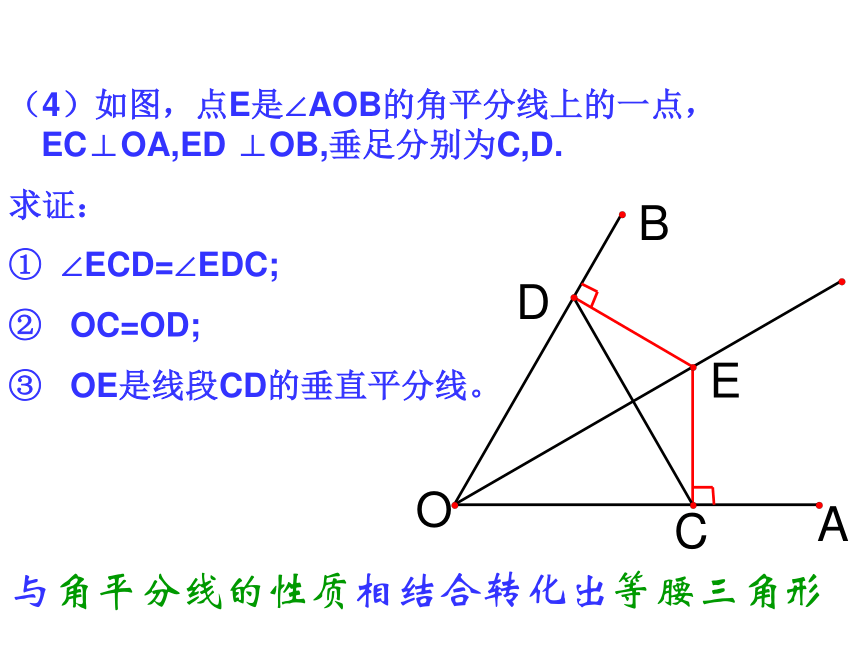
为 cm。3、等腰三角形有一个内角为70°,则一个底角为 度。4、等腰三角形有一个 内角为100°,则一个底角为 度。1或310或111070或5540一、分类思想(1)如图,∠A=∠B,CE∥DA,CE交AB于E, 求证:?CEB是等腰三角形与平行线相结合转化出等腰三角形DAEBC二、转化思想(2)如图,已知CE、CF分别平分∠ACB和它的外角,EF∥BC,EF交AC于D,你能说明DE=DF的理由吗?与平行线、角平分线相结合转化出等腰三角形基本构图:角平分线+平行线构成等腰三角形.(3)如图AB=AC, ∠A=40°,AB的垂直平分线交AC于点D,求∠DBC 的度数。与线段垂直平分线的性质相结合转化出等腰三角形ABCD(4)如图,点E是∠AOB的角平分线上的一点, EC⊥OA,ED ⊥OB,垂足分别为C,D.
求证:
∠ECD=∠EDC;
OC=OD;
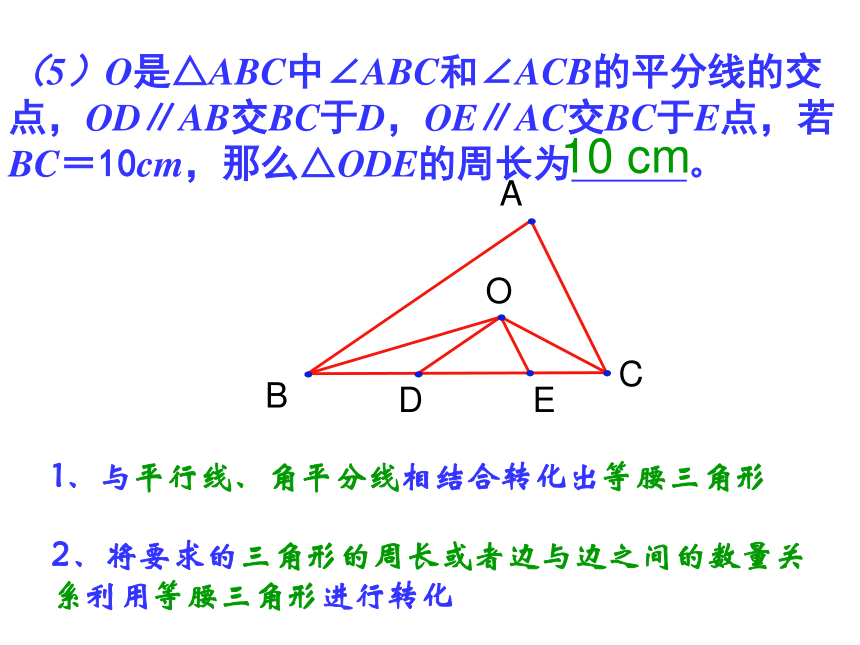
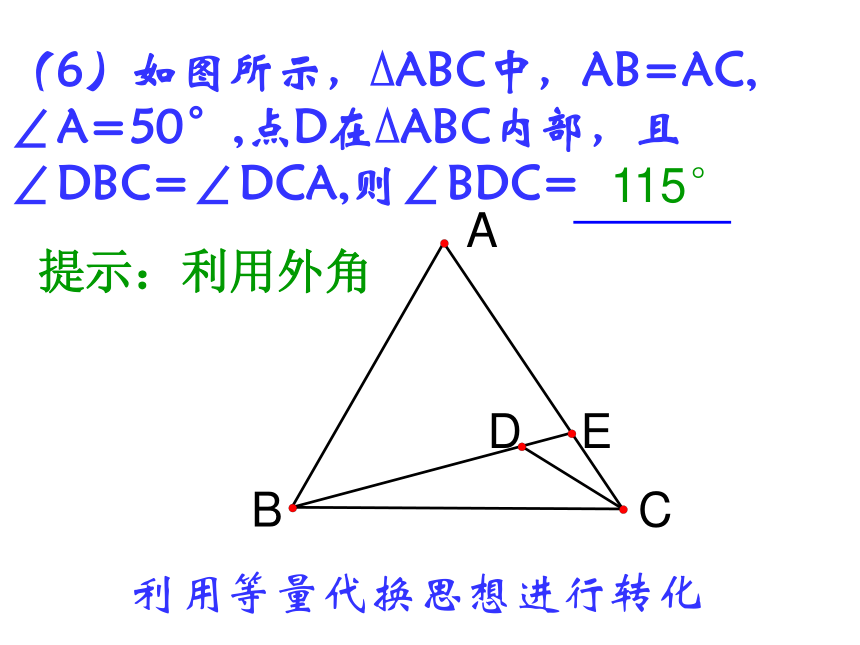
③ OE是线段CD的垂直平分线。与角平分线的性质相结合转化出等腰三角形(5)O是△ABC中∠ABC和∠ACB的平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E点,若BC=10cm,那么△ODE的周长为 。?10 cm1、与平行线、角平分线相结合转化出等腰三角形2、将要求的三角形的周长或者边与边之间的数量关系利用等腰三角形进行转化(6)如图所示,?ABC中,AB=AC, ∠A=50°,点D在?ABC内部,且∠DBC=∠DCA,则∠BDC=115°利用等量代换思想进行转化CABED提示:利用外角二、转化思想1、与平行线、角平分线相结合转化出等腰三角形3、将要求的三角形的周长或者边与边之间的数量关系利用等腰三角形进行转化2、与角平分线的性质、线段垂直平分线的性质相结合转化出等腰三角形4、利用等量代换思想进行转化(1)如图,在△ABC中,AB=AC,AD=BD=BC,则∠A= 度。 36xxx2x2x 三、方程思想(2)如图,在△ABC中,AB=AC,
点D、E分别在AC、AB上,且BC=BD=DE=EA,求 ∠A的度数。
ABCDE(1)已知:如图, AB=AC,DB=DC
证明: ∠C=∠BABCD∠C=∠BBD=CD
克服思维定势,巧妙构造辅助线 四、辅助线思想(2)已知:如图,点D、E在△ABC的边BC上,AB=AC,AD=AE,你能判断出BD与CE相等吗?请说出你判断的理由。 解: BD=CE。
作AF⊥BC,,垂足为F,则AF⊥DE
因为AB=AC,AD=AE(已知)
AF⊥BC,AF⊥DE(辅助线作法)
所以BF=CF,DF=EF(等腰三角形底边上的高与底边上的中线互相重合)
所以BD=CE。
FDECBA1、等腰三角形腰上的高与底边的夹角为α,则顶角β与α之间的关系是2、一个等腰三角形顶角为钝角,则它的底角α的取值范围是3、等腰三角形两底角平分线相等吗?两腰上的中线呢?两腰上的高呢?五、画图思想β=2 α0°< α <45°在等腰△ABC中,AB=AC,若过B、C两点分别作BE⊥AC
于E,CF⊥AB于F,则BE=CF吗?请说明理由。∵AB=AC
∴CF=BE解:S△ABC= AB·CF
S△ABC= AC·BE
即 AB·CF= AC·BE等积法六、其它思想FECBA练习判断下列语句是否正确。(1)等腰三角形的角平分线、中线和高互相重合。( )
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°. ( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××作业(3)如图,在等腰直角三角形ABC中,∠C=90°,AC=BC,AE平分∠BAC,ED⊥AB于点E。1、若CE=2,则DE=____,DB=___2、你还能找出图中哪些相等的线段?3、若AB=8,则ΔDEB的周长为多少?22(AD=AC=BC)ΔDEB的周长=DE+BE+BD
=CE+BE+BD
=BC+BD
=AD+BD=8(CE=DE=BD)F(4) 如图,AB=AC,D为AB上一点,E为AC延长线上一点,且BD=CE,DE交BC于G 求证:DG=EGGCABED (5)在?ABC中,∠BAC=120°,
AD⊥BC于D,且AB+BD=DC, 则∠C的大小是ABCD6。已知:在△ABC中,E是CA延长
上的点,且AB = AC ,
AE = AD。请说明:1)∠BAC=2∠ E。
2)ED⊥BCABCD提高练习:E总结二、转化思想五、画图思想 四、辅助线思想一、分类思想 三、方程思想做一个有思想的人,你才能走的更远。有两边相等的三角形是等腰三角形。性质定理1 :
等边对等角
∵AB = AC
∴∠B=∠C性质定理2: 三线合一。
若AD是底边的高,则AD是顶角平分线,是底边中线
若AD是顶角平分线,则AD是底边的高与中线
若AD是底边中线,则AD是顶角平分线,是底边的高定理:等角对等边
∵ ∠B=∠C
∴ AB = AC等腰三角形相关知识∵ AB=AC, AD ⊥ BC∵ AB=AC , ∠1=∠2“三线合一”的数学语言(3)若AD是高,则AD是角平分线,是中线(1)若AD是角平分线,则AD是高,是中线(2) 若AD是中线,则AD是角平分线,是高∵ AB=AC, BD=CDAB=ACH(2) 如图点E,请在AD上找一点P,使得
PB+PE最小. 如图,在△ABC中,AB=AC, D为底边BC的中点,DE⊥AB, DF⊥AC, DE=DF吗? 书本原题CDBA(1) 点E、F关于AD对称吗?如果是,
请说明理由. (-2,0)(-1,2)(1,2) 如图,在△ABC中,AB=AC, D为底边BC的中点. 书本原题变式1:平移直线AD,使得它与AB交于点E,
与CA的延长线交于点F,则AE=AF吗? EF 如图,在△ABC中,AB=AC, D为底边BC的中点. 书本原题CDBA变式1:平移直线AD,使得它与AB交于点E,
与CA的延长线交于点F,则AE=AF吗? EFH角平分线+平行线三角形中角的2倍关系构成等腰三角形的基本图形 如图,在△ABC中,AB=AC, D为底边BC的中点. 书本原题CDBA变式1:平移直线AD,使得它与AB交于点E,
与CA的延长线交于点F,则AE=AF吗? EFH变式2:继续平移FH至如图形状, AE=AF仍成立吗? 对于Rt△FBC来说,你还
能发现什么结论吗? 变式3:若FE刚好移至如图形状, AE(AB)=AF仍成立吗? 如图,在△ABC中,AB=AC, D为底边BC的中点. 书本原题CDBA变式1:平移直线AD,使得它与AB交于点E,
与CA的延长线交于点F,则AE=AF吗? EF变式2:继续平移FH至如图形状, AE=AF仍成立吗? 直角三角形斜边上的
中线等于斜边的一半. 不经历风雨,怎么见彩虹没有人能随随便便便成功!再见待续…
而是不断的学习.----高斯12.3.1等腰三角形的复习复习概念一、等腰三角形的定义:有两边相等的三角形是等腰三角形二、等腰三角形的性质:1、等腰三角形的 相等,简写为2、等腰三角形的 互相重合,简写 成两个底角等边对等角顶角平分线底边上的中线底边上的高等腰三角形三线合一3、等腰三角形是 图形,对称轴是 所在的直线。轴对称三、等腰三角形的判定1、有两边相等的三角形是等腰三角形 2、有两角相等的三角形是等腰三角形,简写成等角对等边顶角平分线底边上的高D底边上的中线顶角平分线复习性质与判定数学学习中,最主要的就是思维方法的培养,只埋头做题,不注意总结反思,成绩是不会有很大提高的,做题不是莽撞的思考,而是有一定规律的。希望每一个同学都做一个学习上的有心人。等腰三角形部分用了哪些数学思想呢?基础知识点的理解与熟记+大量的做题+不断的总结
=数学高手数学思想5、等腰三角形有 条对称轴。1、等腰三角形有两边长分别为3cm、4cm,则周长
为 cm。2、等腰三角形有两边长分别为2cm、4cm,则周长
为 cm。3、等腰三角形有一个内角为70°,则一个底角为 度。4、等腰三角形有一个 内角为100°,则一个底角为 度。1或310或111070或5540一、分类思想(1)如图,∠A=∠B,CE∥DA,CE交AB于E, 求证:?CEB是等腰三角形与平行线相结合转化出等腰三角形DAEBC二、转化思想(2)如图,已知CE、CF分别平分∠ACB和它的外角,EF∥BC,EF交AC于D,你能说明DE=DF的理由吗?与平行线、角平分线相结合转化出等腰三角形基本构图:角平分线+平行线构成等腰三角形.(3)如图AB=AC, ∠A=40°,AB的垂直平分线交AC于点D,求∠DBC 的度数。与线段垂直平分线的性质相结合转化出等腰三角形ABCD(4)如图,点E是∠AOB的角平分线上的一点, EC⊥OA,ED ⊥OB,垂足分别为C,D.
求证:
∠ECD=∠EDC;
OC=OD;
③ OE是线段CD的垂直平分线。与角平分线的性质相结合转化出等腰三角形(5)O是△ABC中∠ABC和∠ACB的平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E点,若BC=10cm,那么△ODE的周长为 。?10 cm1、与平行线、角平分线相结合转化出等腰三角形2、将要求的三角形的周长或者边与边之间的数量关系利用等腰三角形进行转化(6)如图所示,?ABC中,AB=AC, ∠A=50°,点D在?ABC内部,且∠DBC=∠DCA,则∠BDC=115°利用等量代换思想进行转化CABED提示:利用外角二、转化思想1、与平行线、角平分线相结合转化出等腰三角形3、将要求的三角形的周长或者边与边之间的数量关系利用等腰三角形进行转化2、与角平分线的性质、线段垂直平分线的性质相结合转化出等腰三角形4、利用等量代换思想进行转化(1)如图,在△ABC中,AB=AC,AD=BD=BC,则∠A= 度。 36xxx2x2x 三、方程思想(2)如图,在△ABC中,AB=AC,
点D、E分别在AC、AB上,且BC=BD=DE=EA,求 ∠A的度数。
ABCDE(1)已知:如图, AB=AC,DB=DC
证明: ∠C=∠BABCD∠C=∠BBD=CD
克服思维定势,巧妙构造辅助线 四、辅助线思想(2)已知:如图,点D、E在△ABC的边BC上,AB=AC,AD=AE,你能判断出BD与CE相等吗?请说出你判断的理由。 解: BD=CE。
作AF⊥BC,,垂足为F,则AF⊥DE
因为AB=AC,AD=AE(已知)
AF⊥BC,AF⊥DE(辅助线作法)
所以BF=CF,DF=EF(等腰三角形底边上的高与底边上的中线互相重合)
所以BD=CE。
FDECBA1、等腰三角形腰上的高与底边的夹角为α,则顶角β与α之间的关系是2、一个等腰三角形顶角为钝角,则它的底角α的取值范围是3、等腰三角形两底角平分线相等吗?两腰上的中线呢?两腰上的高呢?五、画图思想β=2 α0°< α <45°在等腰△ABC中,AB=AC,若过B、C两点分别作BE⊥AC
于E,CF⊥AB于F,则BE=CF吗?请说明理由。∵AB=AC
∴CF=BE解:S△ABC= AB·CF
S△ABC= AC·BE
即 AB·CF= AC·BE等积法六、其它思想FECBA练习判断下列语句是否正确。(1)等腰三角形的角平分线、中线和高互相重合。( )
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°. ( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××作业(3)如图,在等腰直角三角形ABC中,∠C=90°,AC=BC,AE平分∠BAC,ED⊥AB于点E。1、若CE=2,则DE=____,DB=___2、你还能找出图中哪些相等的线段?3、若AB=8,则ΔDEB的周长为多少?22(AD=AC=BC)ΔDEB的周长=DE+BE+BD
=CE+BE+BD
=BC+BD
=AD+BD=8(CE=DE=BD)F(4) 如图,AB=AC,D为AB上一点,E为AC延长线上一点,且BD=CE,DE交BC于G 求证:DG=EGGCABED (5)在?ABC中,∠BAC=120°,
AD⊥BC于D,且AB+BD=DC, 则∠C的大小是ABCD6。已知:在△ABC中,E是CA延长
上的点,且AB = AC ,
AE = AD。请说明:1)∠BAC=2∠ E。
2)ED⊥BCABCD提高练习:E总结二、转化思想五、画图思想 四、辅助线思想一、分类思想 三、方程思想做一个有思想的人,你才能走的更远。有两边相等的三角形是等腰三角形。性质定理1 :
等边对等角
∵AB = AC
∴∠B=∠C性质定理2: 三线合一。
若AD是底边的高,则AD是顶角平分线,是底边中线
若AD是顶角平分线,则AD是底边的高与中线
若AD是底边中线,则AD是顶角平分线,是底边的高定理:等角对等边
∵ ∠B=∠C
∴ AB = AC等腰三角形相关知识∵ AB=AC, AD ⊥ BC∵ AB=AC , ∠1=∠2“三线合一”的数学语言(3)若AD是高,则AD是角平分线,是中线(1)若AD是角平分线,则AD是高,是中线(2) 若AD是中线,则AD是角平分线,是高∵ AB=AC, BD=CDAB=ACH(2) 如图点E,请在AD上找一点P,使得
PB+PE最小. 如图,在△ABC中,AB=AC, D为底边BC的中点,DE⊥AB, DF⊥AC, DE=DF吗? 书本原题CDBA(1) 点E、F关于AD对称吗?如果是,
请说明理由. (-2,0)(-1,2)(1,2) 如图,在△ABC中,AB=AC, D为底边BC的中点. 书本原题变式1:平移直线AD,使得它与AB交于点E,
与CA的延长线交于点F,则AE=AF吗? EF 如图,在△ABC中,AB=AC, D为底边BC的中点. 书本原题CDBA变式1:平移直线AD,使得它与AB交于点E,
与CA的延长线交于点F,则AE=AF吗? EFH角平分线+平行线三角形中角的2倍关系构成等腰三角形的基本图形 如图,在△ABC中,AB=AC, D为底边BC的中点. 书本原题CDBA变式1:平移直线AD,使得它与AB交于点E,
与CA的延长线交于点F,则AE=AF吗? EFH变式2:继续平移FH至如图形状, AE=AF仍成立吗? 对于Rt△FBC来说,你还
能发现什么结论吗? 变式3:若FE刚好移至如图形状, AE(AB)=AF仍成立吗? 如图,在△ABC中,AB=AC, D为底边BC的中点. 书本原题CDBA变式1:平移直线AD,使得它与AB交于点E,
与CA的延长线交于点F,则AE=AF吗? EF变式2:继续平移FH至如图形状, AE=AF仍成立吗? 直角三角形斜边上的
中线等于斜边的一半. 不经历风雨,怎么见彩虹没有人能随随便便便成功!再见待续…
