等腰三角形
图片预览








文档简介
课件22张PPT。等腰三角形
高都中学
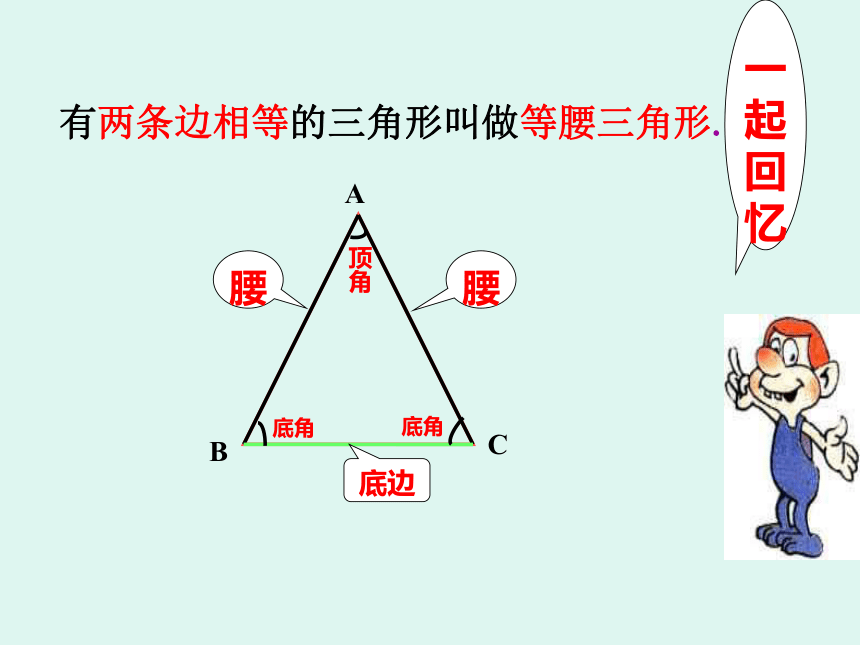
唐爱华请你欣赏北京五塔寺西安半坡博物馆有两条边相等的三角形叫做等腰三角形. 底边一起回忆学习目标探究等腰三角形的性质
在探究学习中养成乐于思维的良好习惯,
学会合作,寻求多种解决问题的方法
培养自己分析问题,解决问题和将知识应用于实际生活的能力
心灵手巧材料: 一张矩形纸方法:(1)先将矩形纸按图中虚线对折;
(2)裁掉阴影部分; (3)将剩余部分展开。
沿刚才的折痕再折叠,
刚才得到的三角形是轴对称图形吗?
找出其中重合的线段和角.D 探索 :你发现了什么? 大胆猜想根据刚才你发现的重合的
角和线段,猜想:
等腰三角形有哪些性质呢? 等腰三角形的性质1:等腰三角形的两个底角相等
(等边对等角 )。
等腰三角形的性质2: 等腰三角形顶角的平分线, 底边上的中线,底边上的高互相重合(三线合一)
(1)作顶角∠ BAC的角平分线,使得∠1 = ∠ 2 , (2)作底边BC的中线 ,使得BD=CD , 议一议:有哪些方法可以证明∠B = ∠C呢? 用数学符号语言改写等腰三角形性质2,
在等腰ΔABC中,AB=AC,
(1)∵ AB=AC AD⊥BC,
∴ ∠____=∠____,___=____;
(2)∵ AB=AC AD是中线,
∴ ____⊥____,∠____=∠____;
(3)∵ AB=AC AD是角平分线,
∴ ____⊥____,____ = _____。
BAD CAD BD CDAD BC BAD CADAD BC BD CD1等腰三角形的两边长分别为3和7,则第三边的长为____
2若等腰三角形的一边等于5,另一边为6,则它的周长为____
3已知等腰三角形的一个角是36°则其余两角为____
4已知等腰三角形的一个角是110°,则其余两角为____
716或1736°、108°或72°、72°35°、35°如图,△ABC是等腰直角三角(AB=AC∠BAC=90°)。AD是底边BC的高,标出∠ B, ∠ C, ∠ BAD, ∠CAD的度数,图中有哪些相等的线段?ACB∟∟D45°45°45°45°相等的线段:
AB=AC
AD=BD=CD例如图:在△ABC中,AB=AC,点D在AC上, 且BD=BC=AD. 求:△ABC各角的度数
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,
∠A=∠ABD(等边对等角).
设∠ A=x,则
∠BDC=∠A+∠ABD=2x,
从而 ∠ABC=∠C=∠BDC=2x.
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180°
解得 x=36 °.
在△ABC中, ∠A=36 °, ∠ABC=∠C=72 °.DCBA在△ABC中,AB=AD=DC,∠BAD=26°, 求∠ B 和∠ C的度数。∠ B=77° ∠ C=33.5°已知:如图AB=AC,AD=AE。求证:BD=CEABDEC方法二:
证明: ∵AB=AC
∴∠B=∠C(等边对等角)
同理:∠ADE=∠AED
又∵ ∠ADE+∠ADB=180°
∠AED+∠AEC=180 °
∠ADB= ∠ AEC(等角的补角相等)
在△ABD与△ ACD中
∵ ∠B=∠C
∠ADB=∠AEC
AD=AE
∴ △ ABD≌ △ ACE(AAS)
∴ BD=CE方法一:
过A作AF⊥BC垂足为F点,
∵ AB=AC
∴BF=FC(三线合一)
同理:DF=EF
∴BF-DF=FC-EF
即BD=CEF 你收获了什么?根据本节课所学等腰三角形的性质思考并总结:
1在等腰三角形中知道了顶角如何求底角? 知道了底角如何求顶角?
2在等腰三角形的有关题目中,我们可以有哪些 辅助线的作法?
演示如图的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,调整架身,使点A恰好在重锤线上。这时BC处于水平位置,为什么?
生活小常识:地震后,如何用这个测平架检测教室的房梁是否水平呢?愿同学们的学习
步步登高
高都中学
唐爱华请你欣赏北京五塔寺西安半坡博物馆有两条边相等的三角形叫做等腰三角形. 底边一起回忆学习目标探究等腰三角形的性质
在探究学习中养成乐于思维的良好习惯,
学会合作,寻求多种解决问题的方法
培养自己分析问题,解决问题和将知识应用于实际生活的能力
心灵手巧材料: 一张矩形纸方法:(1)先将矩形纸按图中虚线对折;
(2)裁掉阴影部分; (3)将剩余部分展开。
沿刚才的折痕再折叠,
刚才得到的三角形是轴对称图形吗?
找出其中重合的线段和角.D 探索 :你发现了什么? 大胆猜想根据刚才你发现的重合的
角和线段,猜想:
等腰三角形有哪些性质呢? 等腰三角形的性质1:等腰三角形的两个底角相等
(等边对等角 )。
等腰三角形的性质2: 等腰三角形顶角的平分线, 底边上的中线,底边上的高互相重合(三线合一)
(1)作顶角∠ BAC的角平分线,使得∠1 = ∠ 2 , (2)作底边BC的中线 ,使得BD=CD , 议一议:有哪些方法可以证明∠B = ∠C呢? 用数学符号语言改写等腰三角形性质2,
在等腰ΔABC中,AB=AC,
(1)∵ AB=AC AD⊥BC,
∴ ∠____=∠____,___=____;
(2)∵ AB=AC AD是中线,
∴ ____⊥____,∠____=∠____;
(3)∵ AB=AC AD是角平分线,
∴ ____⊥____,____ = _____。
BAD CAD BD CDAD BC BAD CADAD BC BD CD1等腰三角形的两边长分别为3和7,则第三边的长为____
2若等腰三角形的一边等于5,另一边为6,则它的周长为____
3已知等腰三角形的一个角是36°则其余两角为____
4已知等腰三角形的一个角是110°,则其余两角为____
716或1736°、108°或72°、72°35°、35°如图,△ABC是等腰直角三角(AB=AC∠BAC=90°)。AD是底边BC的高,标出∠ B, ∠ C, ∠ BAD, ∠CAD的度数,图中有哪些相等的线段?ACB∟∟D45°45°45°45°相等的线段:
AB=AC
AD=BD=CD例如图:在△ABC中,AB=AC,点D在AC上, 且BD=BC=AD. 求:△ABC各角的度数
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,
∠A=∠ABD(等边对等角).
设∠ A=x,则
∠BDC=∠A+∠ABD=2x,
从而 ∠ABC=∠C=∠BDC=2x.
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180°
解得 x=36 °.
在△ABC中, ∠A=36 °, ∠ABC=∠C=72 °.DCBA在△ABC中,AB=AD=DC,∠BAD=26°, 求∠ B 和∠ C的度数。∠ B=77° ∠ C=33.5°已知:如图AB=AC,AD=AE。求证:BD=CEABDEC方法二:
证明: ∵AB=AC
∴∠B=∠C(等边对等角)
同理:∠ADE=∠AED
又∵ ∠ADE+∠ADB=180°
∠AED+∠AEC=180 °
∠ADB= ∠ AEC(等角的补角相等)
在△ABD与△ ACD中
∵ ∠B=∠C
∠ADB=∠AEC
AD=AE
∴ △ ABD≌ △ ACE(AAS)
∴ BD=CE方法一:
过A作AF⊥BC垂足为F点,
∵ AB=AC
∴BF=FC(三线合一)
同理:DF=EF
∴BF-DF=FC-EF
即BD=CEF 你收获了什么?根据本节课所学等腰三角形的性质思考并总结:
1在等腰三角形中知道了顶角如何求底角? 知道了底角如何求顶角?
2在等腰三角形的有关题目中,我们可以有哪些 辅助线的作法?
演示如图的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,调整架身,使点A恰好在重锤线上。这时BC处于水平位置,为什么?
生活小常识:地震后,如何用这个测平架检测教室的房梁是否水平呢?愿同学们的学习
步步登高
