(新人教版选修1-1)数学:1.2充分条件与必要条件(课件)
文档属性
| 名称 | (新人教版选修1-1)数学:1.2充分条件与必要条件(课件) |  | |
| 格式 | rar | ||
| 文件大小 | 49.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-01 16:56:00 | ||
图片预览






文档简介
课件16张PPT。1.2《充分条件和必要条件》 教学目标 知识目标:
1、正确理解充分条件、必要条件、充要条件三个概念。
2、能利用充分条件、必要条件、充要条件三个概念,熟练判断四种命题间的关系。
3、在理解定义的基础上,可以自觉地对定义进行转化,转化成推理关系及集合的包含关系。
(二)能力目标:
1、培养学生的观察与类比能力:“会观察”,通过大量的问题,会观察其共性及个性。
2、培养学生的归纳能力:“敢归纳”,敢于对一些事例,观察后进行归纳,总结出一般规律。
3、培养学生的建构能力:“善建构”,通过反复的观察分析和类比,对归纳出的结论,建构于自己的知识体系中。(三)情感目标:
通过以学生为主体的教学方法,让学生自己构造数学命题,发展体验获取知识的感受。
通过对命题的四种形式及充分条件,必要条件的相对性,培养同学们的辩证唯物主义观点。
3、通过“会观察”,“敢归纳”,“善建构”,培养学生自主学习,勇于创新,多方位审视问题的创造技巧,敢于把错误的思维过程及弱点暴露出来,并在问题面前表现出浓厚的兴趣和不畏困难、勇于进取的精神。
【教学重点】构建充分条件、必要条件的数学意义;
【教学难点】命题条件的充分性、必要性的判断
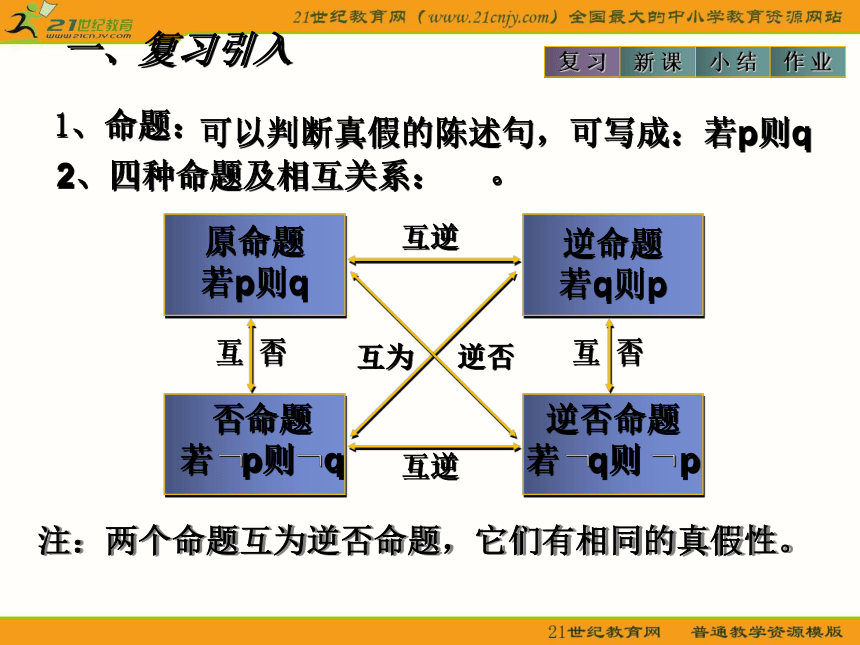
1、命题:可以判断真假的陈述句,可写成:若p则q。 2、四种命题及相互关系:一、复习引入 小 结作 业复 习新 课注:两个命题互为逆否命题,它们有相同的真假性。一、复习引入小 结作 业复 习新 课3、例 :判断下列命题的真假。 (1)若x>a2+b2,则x>2ab 。 (2)若ab=0,则a=0。(2)因为若ab=0 则应该有a=0 或b=0。
所以并不能得到a一定为0。真命题假命题解(1)因为若x>a2+b2 ,而a2+b2 2ab,所以可以
得到 x>2ab 。 一、复习引入小 结作 业复 习新 课4、例, 将(1)改写成“若p,则q”的形式 并判断下列命题的真假及其逆命题的真假。 (1)有两角相等的三角形是等腰三角形。 (2)若a2>b2,则a>b。解(1)原命题:若一个三角形有两个角相等,则这个
三角形是等腰三角形。(2)原命题:若a2>b2,则a>b。逆命题:若一个三角形是等腰三角形,则这个
三 角形有两个角相等。逆命题:若a>b,则a2>b2。真命题真命题假命题假命题一、复习引入 在真命题(1)中,p是q成立所必须具备的前提。 在假命题(2)中,p不是q成立所必须具备的前提。 在真命题(1)中,p足以导致q,也就是说条件p充分了。 在假命题(2)中条件p不充分。(1)有两角相等的三角形是等腰三角形。 (2)若a2>b2,则a>b。小 结作 业复 习新 课二、新课 小 结作 业新 课复 习练习1 用符号 与 填空。 (1) x2=y2 x=y; (2)内错角相等 两直线平行; (3)整数a能被6整除 a的个位数字为偶数;(4)ac=bc a=b 二、新课 复 习小 结作 业新 课二、新课 例1,下列“若p,则q”形式的命题中,哪些命题 中的p是q的充分条件? (1)若x=1,则x2 –4x+3=0; (2)若f(x)=x,则f(x)为增函数; (3)若x 为无理数,则x2 为无理数解:命题(1)(2)是真命题,命题(3)是假命题,所以命题(1)(2)中的p是q的充分条件复 习小 结作 业新 课二、新课 练习2 下列“若p,则q”形式的命题中,哪些命题中的 p是q的充分条件?复 习小 结作 业新 课(1) 若两个三角形全等,则这两个三角形相似;(2) 若x > 5,则x > 10。解:命题(1)是真命题,命题(2)是假命题
所以命题(1)中的p是q的充分条件。二、新课 复 习小 结作 业新 课① 认清条件和结论。① 可先简化命题。③ 将命题转化为等价的逆否命题后再判断。② 否定一个命题只要举出一个反例即可。判别充分条件与必要条件二、新课 例2 下列“若p,则q”形式的命题中,哪些命题中的 q是p的必要条件?复 习小 结作 业新 课(1) 若x=y,则x2=y2。(2) 若两个三角形全等,则这两个三角形的面积相等。(3) 若a>b,则ac>bc。解:命题(1)(2)是真命题,命题(3)是假命题,
所以命题(1)(2)中的q是p的必要条件。二、新课 练习3 下列“若p,则q”形式的命题中,哪些命题中的 p是q的必要条件?复 习小 结作 业新 课(1) 若a+5是无理数,则a是无理数。(2) 若(x-a)(x-b)=0,则 x=a。解:命题(1)(2)的逆命题都是真命题,
所以命题(1)(2)中的p是q的必要条件。分析:注意这里考虑的是命题中的p是q的必要条件。
所以应该分析下列命题的逆命题的真假性。二、新课 复 习小 结作 业新 课答:命题(1)为真命题:命题(2)为真命题;命题(3)为假命题;命题(4)为真命题。三、小结 ① 认清条件和结论。① 可先简化命题。③ 将命题转化为等价的逆否命题后再判断。② 否定一个命题只要举出一个反例即可。1、定义:新 课复 习作 业小 结
1、正确理解充分条件、必要条件、充要条件三个概念。
2、能利用充分条件、必要条件、充要条件三个概念,熟练判断四种命题间的关系。
3、在理解定义的基础上,可以自觉地对定义进行转化,转化成推理关系及集合的包含关系。
(二)能力目标:
1、培养学生的观察与类比能力:“会观察”,通过大量的问题,会观察其共性及个性。
2、培养学生的归纳能力:“敢归纳”,敢于对一些事例,观察后进行归纳,总结出一般规律。
3、培养学生的建构能力:“善建构”,通过反复的观察分析和类比,对归纳出的结论,建构于自己的知识体系中。(三)情感目标:
通过以学生为主体的教学方法,让学生自己构造数学命题,发展体验获取知识的感受。
通过对命题的四种形式及充分条件,必要条件的相对性,培养同学们的辩证唯物主义观点。
3、通过“会观察”,“敢归纳”,“善建构”,培养学生自主学习,勇于创新,多方位审视问题的创造技巧,敢于把错误的思维过程及弱点暴露出来,并在问题面前表现出浓厚的兴趣和不畏困难、勇于进取的精神。
【教学重点】构建充分条件、必要条件的数学意义;
【教学难点】命题条件的充分性、必要性的判断
1、命题:可以判断真假的陈述句,可写成:若p则q。 2、四种命题及相互关系:一、复习引入 小 结作 业复 习新 课注:两个命题互为逆否命题,它们有相同的真假性。一、复习引入小 结作 业复 习新 课3、例 :判断下列命题的真假。 (1)若x>a2+b2,则x>2ab 。 (2)若ab=0,则a=0。(2)因为若ab=0 则应该有a=0 或b=0。
所以并不能得到a一定为0。真命题假命题解(1)因为若x>a2+b2 ,而a2+b2 2ab,所以可以
得到 x>2ab 。 一、复习引入小 结作 业复 习新 课4、例, 将(1)改写成“若p,则q”的形式 并判断下列命题的真假及其逆命题的真假。 (1)有两角相等的三角形是等腰三角形。 (2)若a2>b2,则a>b。解(1)原命题:若一个三角形有两个角相等,则这个
三角形是等腰三角形。(2)原命题:若a2>b2,则a>b。逆命题:若一个三角形是等腰三角形,则这个
三 角形有两个角相等。逆命题:若a>b,则a2>b2。真命题真命题假命题假命题一、复习引入 在真命题(1)中,p是q成立所必须具备的前提。 在假命题(2)中,p不是q成立所必须具备的前提。 在真命题(1)中,p足以导致q,也就是说条件p充分了。 在假命题(2)中条件p不充分。(1)有两角相等的三角形是等腰三角形。 (2)若a2>b2,则a>b。小 结作 业复 习新 课二、新课 小 结作 业新 课复 习练习1 用符号 与 填空。 (1) x2=y2 x=y; (2)内错角相等 两直线平行; (3)整数a能被6整除 a的个位数字为偶数;(4)ac=bc a=b 二、新课 复 习小 结作 业新 课二、新课 例1,下列“若p,则q”形式的命题中,哪些命题 中的p是q的充分条件? (1)若x=1,则x2 –4x+3=0; (2)若f(x)=x,则f(x)为增函数; (3)若x 为无理数,则x2 为无理数解:命题(1)(2)是真命题,命题(3)是假命题,所以命题(1)(2)中的p是q的充分条件复 习小 结作 业新 课二、新课 练习2 下列“若p,则q”形式的命题中,哪些命题中的 p是q的充分条件?复 习小 结作 业新 课(1) 若两个三角形全等,则这两个三角形相似;(2) 若x > 5,则x > 10。解:命题(1)是真命题,命题(2)是假命题
所以命题(1)中的p是q的充分条件。二、新课 复 习小 结作 业新 课① 认清条件和结论。① 可先简化命题。③ 将命题转化为等价的逆否命题后再判断。② 否定一个命题只要举出一个反例即可。判别充分条件与必要条件二、新课 例2 下列“若p,则q”形式的命题中,哪些命题中的 q是p的必要条件?复 习小 结作 业新 课(1) 若x=y,则x2=y2。(2) 若两个三角形全等,则这两个三角形的面积相等。(3) 若a>b,则ac>bc。解:命题(1)(2)是真命题,命题(3)是假命题,
所以命题(1)(2)中的q是p的必要条件。二、新课 练习3 下列“若p,则q”形式的命题中,哪些命题中的 p是q的必要条件?复 习小 结作 业新 课(1) 若a+5是无理数,则a是无理数。(2) 若(x-a)(x-b)=0,则 x=a。解:命题(1)(2)的逆命题都是真命题,
所以命题(1)(2)中的p是q的必要条件。分析:注意这里考虑的是命题中的p是q的必要条件。
所以应该分析下列命题的逆命题的真假性。二、新课 复 习小 结作 业新 课答:命题(1)为真命题:命题(2)为真命题;命题(3)为假命题;命题(4)为真命题。三、小结 ① 认清条件和结论。① 可先简化命题。③ 将命题转化为等价的逆否命题后再判断。② 否定一个命题只要举出一个反例即可。1、定义:新 课复 习作 业小 结
