高一(人教a版)数学课件:1.1.2集合间的基本关系
文档属性
| 名称 | 高一(人教a版)数学课件:1.1.2集合间的基本关系 |

|
|
| 格式 | rar | ||
| 文件大小 | 733.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-01 00:00:00 | ||
图片预览







文档简介
课件25张PPT。1.1.2 集合间的基本关系
1.集合的表示方法有 、 .
2.元素与集合间的关系用符号 或 表示.
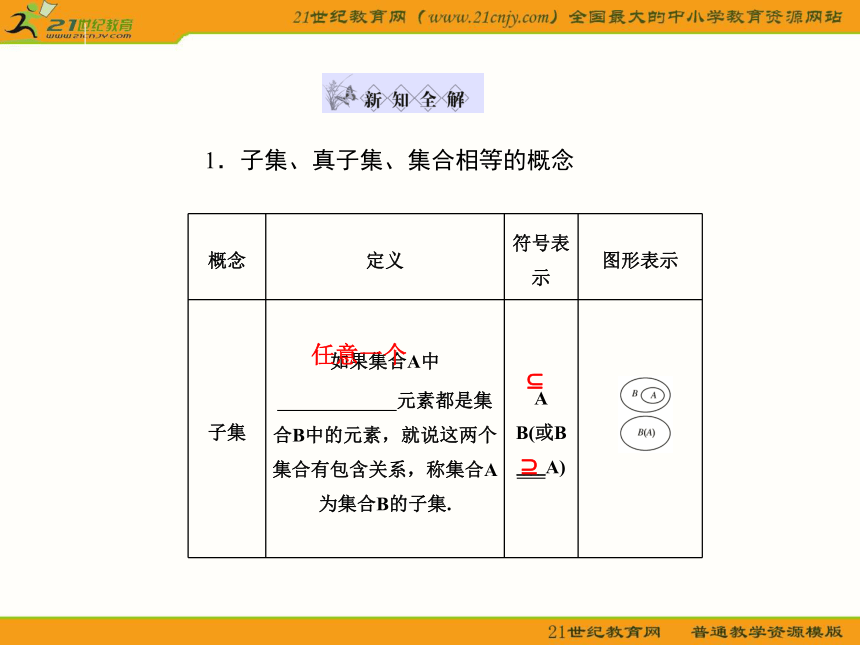
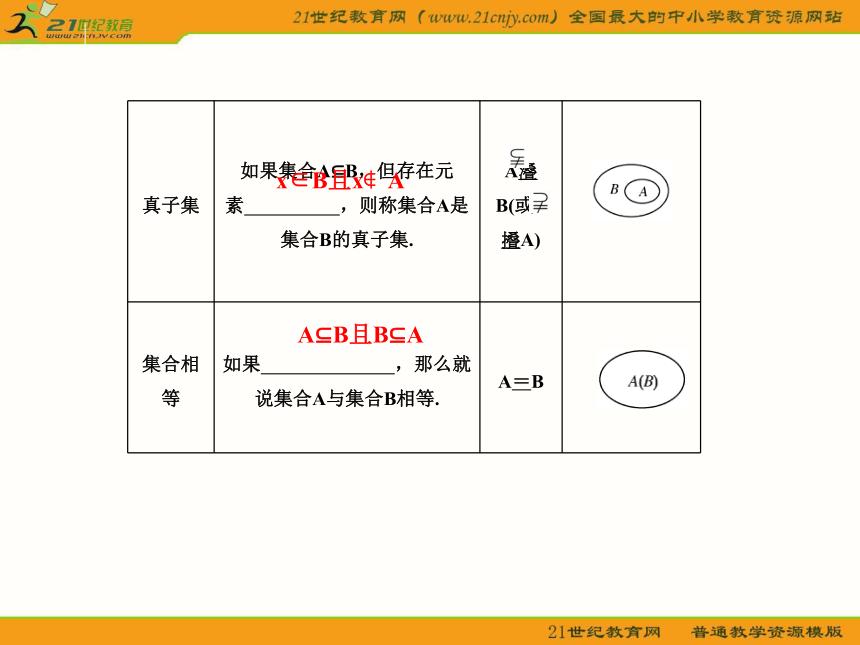
3.两个集合相等是指 .列举法描述法∈?构成集合的元素相同1.子集、真子集、集合相等的概念
任意一个??x∈B且x?AA?B且B?A2.空集
(1)定义: 的集合,叫做空集.
(2)用符号表示为: .
(3)规定:空集是任何集合的 .
3.子集的有关性质
(1)任何一个集合是它本身的_______,即 .
(2)对于集合A,B,C,如果A?B,B?C,那么 .不含任何元素子集子集A?AA?C?1.能否把“A?B”理解成“A是B中部分元素组成的集合”?
【提示】 不能.这是因为当A=?时,A?B,但A中不含任何元素;又当A=B时,也有A?B,但A中含有B中的所有元素,这两种情况都有A?B成立,所以上述理解是错误的.2.包含关系{a}?A与从属关系a∈A有什么区别?
【提示】 两者的区别是(1)从符号上看,“?”表示的是两个集合之间的关系,“∈”表示的是元素与集合之间的关系;(2){a}是有一个元素的集合,而a通常表示一个元素;(3){a}?A表示{a}是A的一个子集,而a∈A表示a是A的一个元素.【答案】 -1(1)两个集合相等,则所含元素完全相同,与顺序无关,但要注意检验,排除与集合元素互异性或与已知相矛盾的情形.
(2)若两个集合中元素均无限多个,要看两集合的代表元素是否一致,且看代表元素满足的条件是否一致,若均一致,则两集合相等.1.设集合A={1,-2,a2-1},B={1,a2-3a,0},若A=B,求a的值.写出满足{a,b}?A?{a,b,c,d}的所有集合A.
【思路点拨】 由题目可获取以下主要信息:
①集合{a,b},{a,b,c,d}已知;
②集合A满足{a,b}?A?{a,b,c,d};
③求集合A.
解答本题可根据子集、真子集的概念求解.
【解析】 由题设可知,一方面A是集合{a,b,c,d}的子集,另一方面A又真包含集合{a,b},故集合A中至少含有两个元素a,b,且含有c,d两个元素中的一个或两个.
故满足条件的集合有{a,b,c},{a,b,d},{a,b,c,d}.(1)正确区分子集与真子集概念是解题的关键.
(2)写一个集合的子集时,按子集中元素个数多少,以一定顺序来写不易发生重复和遗漏现象.
(3)集合中含有n个元素,则此集合有2n个子集,记住这个结论可以提高解答速度,其中要注意空集?和集合本身易漏掉.2.若{a,b}?A?{a,b,c,d},写出所有集合A.
【解析】 由题意知A是集合{a,b,c,d}的真子集又A包含集合{a,b},故集合A中至少含有两个元素a,b,最多含有3个元素.
故满足条件的集合有{a,b},{a,b,c},{a,b,d}.已知集合A={x|-3【思路点拨】 由题目可获取以下主要信息:
①集合A是一个定集合,可以在数轴上标出其取值范围;
②集合B是一个动集合,其范围随参数m的变化而变化.
解答本题可先求出集合A中变量x的取值范围,此时需注意对参数m进行讨论,然后借助于数轴分析A?B成立的条件.(1)分析集合关系时,首先要分析、简化每个集合.(2)此类问题通常借助数轴,利用数轴分析法,将各个集合在数轴上表示出来,以形定数,还要注意验证端点值,做到准确无误,一般含“=”用实心点表示,不含“=”用空心点表示.
(3)此类问题还应注意“空集”这一“陷阱”,尤其是集合中含有字母参数时,初学者会想当然认为非空集合而丢解,因此分类讨论思想是必须的.3.本例中,若将“B?A”改为“A?B”,其他条件不变,则实数m的取值范围是什么?
【解析】 显然A≠?,又A?B,∴B≠?,
如图所示,1.子集、空集的概念的理解
(1)集合A是集合B的子集,不能简单地理解为集合A是由集合B的“部分元素”所组成的集合。如A=?,则集合A不含B中的任何元素.
(2)如果集合A中存在着不属于集合B的元素,那么A不包含于B,或B不包含A.这有两方面的含义,其一是A、B互不包含,如A={a,b},B={b,c,d};其二是,A包含B,如A={a,b,c},B={b,c}.(3){0}与?的区别:{0}是含有一个元素的集合,?是不含任何元素的集合.因此,有??{0},不能写成?={0},?∈{0}.
3.两集合相等的证明
若A、B两个集合是元素较少的有限集,可用列举法将元素列举出来,说明两个集合的元素完全相同,从而A=B;若A、B是无限集时,欲证A=B,只需证A?B与B?A都成立即可.【错因】 上述解法是初学者解此类问题的典型错误解法.原因是考虑不全面,由集合B的含义及B?A,忽略了集合为?的可能,而漏掉解.因此题目若出现包含关系时,应首先想到有没有出现?的可能.课时作业
点击进入链接页码以及子标题内容页
1.集合的表示方法有 、 .
2.元素与集合间的关系用符号 或 表示.
3.两个集合相等是指 .列举法描述法∈?构成集合的元素相同1.子集、真子集、集合相等的概念
任意一个??x∈B且x?AA?B且B?A2.空集
(1)定义: 的集合,叫做空集.
(2)用符号表示为: .
(3)规定:空集是任何集合的 .
3.子集的有关性质
(1)任何一个集合是它本身的_______,即 .
(2)对于集合A,B,C,如果A?B,B?C,那么 .不含任何元素子集子集A?AA?C?1.能否把“A?B”理解成“A是B中部分元素组成的集合”?
【提示】 不能.这是因为当A=?时,A?B,但A中不含任何元素;又当A=B时,也有A?B,但A中含有B中的所有元素,这两种情况都有A?B成立,所以上述理解是错误的.2.包含关系{a}?A与从属关系a∈A有什么区别?
【提示】 两者的区别是(1)从符号上看,“?”表示的是两个集合之间的关系,“∈”表示的是元素与集合之间的关系;(2){a}是有一个元素的集合,而a通常表示一个元素;(3){a}?A表示{a}是A的一个子集,而a∈A表示a是A的一个元素.【答案】 -1(1)两个集合相等,则所含元素完全相同,与顺序无关,但要注意检验,排除与集合元素互异性或与已知相矛盾的情形.
(2)若两个集合中元素均无限多个,要看两集合的代表元素是否一致,且看代表元素满足的条件是否一致,若均一致,则两集合相等.1.设集合A={1,-2,a2-1},B={1,a2-3a,0},若A=B,求a的值.写出满足{a,b}?A?{a,b,c,d}的所有集合A.
【思路点拨】 由题目可获取以下主要信息:
①集合{a,b},{a,b,c,d}已知;
②集合A满足{a,b}?A?{a,b,c,d};
③求集合A.
解答本题可根据子集、真子集的概念求解.
【解析】 由题设可知,一方面A是集合{a,b,c,d}的子集,另一方面A又真包含集合{a,b},故集合A中至少含有两个元素a,b,且含有c,d两个元素中的一个或两个.
故满足条件的集合有{a,b,c},{a,b,d},{a,b,c,d}.(1)正确区分子集与真子集概念是解题的关键.
(2)写一个集合的子集时,按子集中元素个数多少,以一定顺序来写不易发生重复和遗漏现象.
(3)集合中含有n个元素,则此集合有2n个子集,记住这个结论可以提高解答速度,其中要注意空集?和集合本身易漏掉.2.若{a,b}?A?{a,b,c,d},写出所有集合A.
【解析】 由题意知A是集合{a,b,c,d}的真子集又A包含集合{a,b},故集合A中至少含有两个元素a,b,最多含有3个元素.
故满足条件的集合有{a,b},{a,b,c},{a,b,d}.已知集合A={x|-3
①集合A是一个定集合,可以在数轴上标出其取值范围;
②集合B是一个动集合,其范围随参数m的变化而变化.
解答本题可先求出集合A中变量x的取值范围,此时需注意对参数m进行讨论,然后借助于数轴分析A?B成立的条件.(1)分析集合关系时,首先要分析、简化每个集合.(2)此类问题通常借助数轴,利用数轴分析法,将各个集合在数轴上表示出来,以形定数,还要注意验证端点值,做到准确无误,一般含“=”用实心点表示,不含“=”用空心点表示.
(3)此类问题还应注意“空集”这一“陷阱”,尤其是集合中含有字母参数时,初学者会想当然认为非空集合而丢解,因此分类讨论思想是必须的.3.本例中,若将“B?A”改为“A?B”,其他条件不变,则实数m的取值范围是什么?
【解析】 显然A≠?,又A?B,∴B≠?,
如图所示,1.子集、空集的概念的理解
(1)集合A是集合B的子集,不能简单地理解为集合A是由集合B的“部分元素”所组成的集合。如A=?,则集合A不含B中的任何元素.
(2)如果集合A中存在着不属于集合B的元素,那么A不包含于B,或B不包含A.这有两方面的含义,其一是A、B互不包含,如A={a,b},B={b,c,d};其二是,A包含B,如A={a,b,c},B={b,c}.(3){0}与?的区别:{0}是含有一个元素的集合,?是不含任何元素的集合.因此,有??{0},不能写成?={0},?∈{0}.
3.两集合相等的证明
若A、B两个集合是元素较少的有限集,可用列举法将元素列举出来,说明两个集合的元素完全相同,从而A=B;若A、B是无限集时,欲证A=B,只需证A?B与B?A都成立即可.【错因】 上述解法是初学者解此类问题的典型错误解法.原因是考虑不全面,由集合B的含义及B?A,忽略了集合为?的可能,而漏掉解.因此题目若出现包含关系时,应首先想到有没有出现?的可能.课时作业
点击进入链接页码以及子标题内容页
