高一(人教a版)数学课件:1.3.1单调性与最大(小)值(第1课时函数的单调性)
文档属性
| 名称 | 高一(人教a版)数学课件:1.3.1单调性与最大(小)值(第1课时函数的单调性) |

|
|
| 格式 | rar | ||
| 文件大小 | 830.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-01 00:00:00 | ||
图片预览






文档简介
课件27张PPT。1.3.1 单调性与最大(小)值(第1课时 函数的单调性)
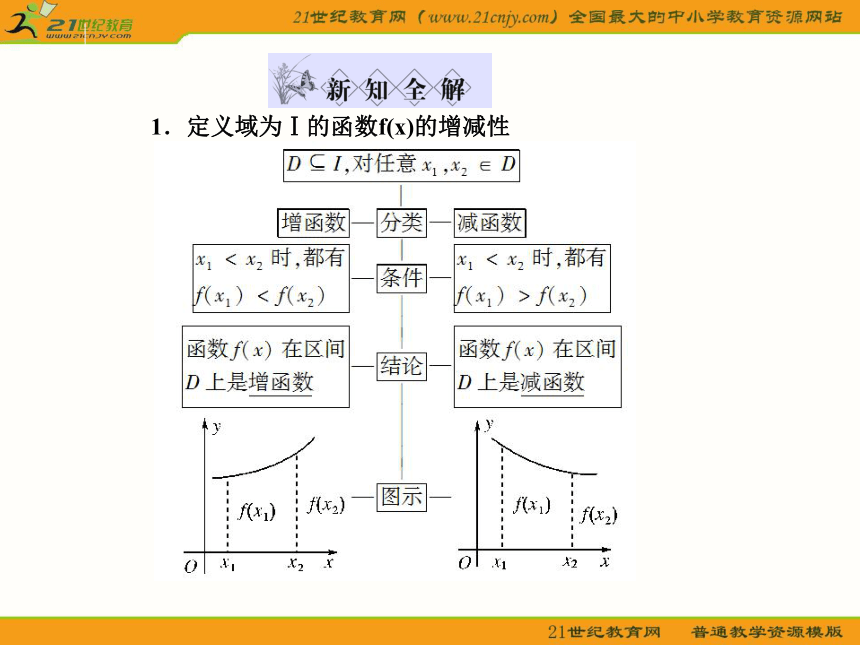
1.定义域为Ⅰ的函数f(x)的增减性2.函数的单调区间
如果函数y=f(x)在区间D上是__________________,那么就说函数y=f(x)在这一区间上具有(严格的)单调性,区间D叫做y=f(x)的____________.增函数(或减函数)单调区间1.在增减函数定义中,能否把“任意两个自变量”改为“存在两个自变量”?
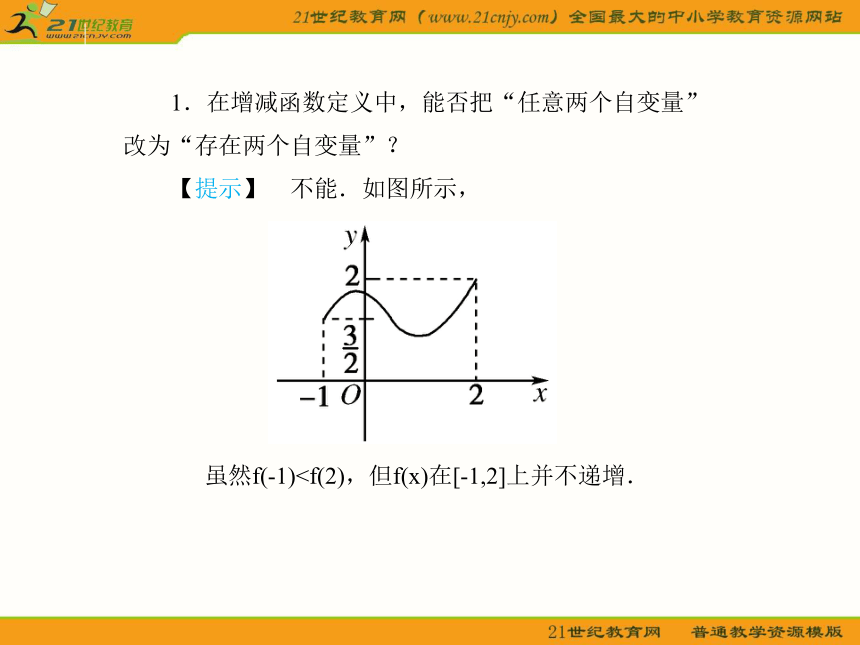
【提示】 不能.如图所示,虽然f(-1)【提示】 (1)函数单调性的判断方法有三种:一是依据单调性的定义;二是依据函数的图象;三是依据已知函数的单调性判断.如已学过的一次函数、二次函数、反比例函数的单调性情况.【思路点拨】 由题目可获取以下主要信息:
①函数解析式中含有根号;
②用定义证明.
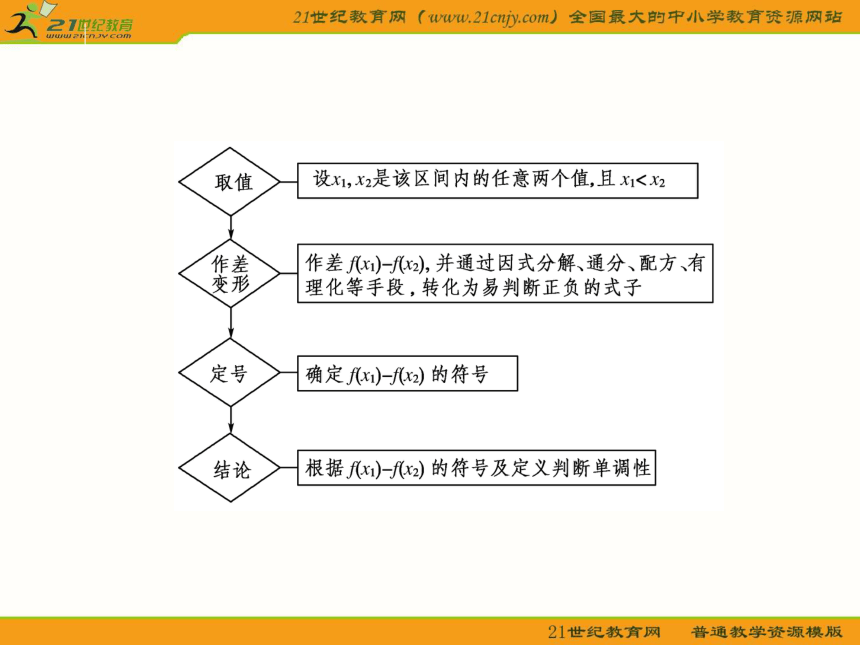
解答本题只需按照函数单调递增的定义加以证明.证明函数单调性的常用方法是定义法或图象法,利用定义法判断函数单调性的步骤为:已知函数y=f(x)的图象如图所示,试根据图象研究函数的单调区间.【思路点拨】 结合图象―→确定单调区间
【解析】 函数的定义域为R,由图象可知,(-∞,-1)和[0,1)是这个函数的递增区间,[-1,0)和[1,+∞)是这个函数的递减区间.(1)利用图象研究函数的单调性是常用的解题方法.但要注意函数的定义域.
(2)写单调区间时,不连续的单调区间必须分开写,不能用“∪”符号连接它们.2.如图为函数y=f(x)的图象,根据图象写出函数的单调区间并判断在每一区间它是增函数还是减函数.【解析】 由函数y=f(x)的图象知单调区间有(-∞,-2),
[-2,1),[1,3)和[3,+∞).其中,在区间(-∞,-2)和[1,3)上函数f(x)为增函数;在区间[-2,1)和[3,+∞)上函数f(x)为减函数.已知函数f(x)=x2-2(a-1)x+3在区间(-∞,4]上是减函数,求实数a的取值范围.
【思路点拨】 由题目可获取以下主要信息:
①所给函数为二次函数,且含有参数;
②函数在区间(-∞,4]上是减函数.
解答本题可先将函数解析式配方,然后找出图象的对称轴,再考虑对称轴与所给区间的位置关系,利用数形结合求解.【解析】 f(x)=x2-2(a-1)x+3
=[x-(a-1)]2-(a-1)2+3,
∴此二次函数的对称轴为x=a-1.
∴f(x)的单调减区间为(-∞,a-1].
∵f(x)在(-∞,4]上是减函数,
∴对称轴x=a-1必须在直线x=4的右侧或与其重合.
∴a-1≥4,解得a≥5.(1)二次函数是常见函数,遇到二次函数后就配方找对称轴,画出图象,会给研究问题带来很大的方便.
(2)已知函数单调性求参数的取值范围,要注意数形结合,采用逆向思维方法.3.本例中,若将函数“在区间(-∞,4]上是减函数”改为“函数的单调递减区间为(-∞,4]”,则a为何值?
【解析】 由例题知函数f(x)的单调递减区间为(-∞,1-a],
∴a-1=4,a=5.1.解读函数单调性的定义
(1)定义中的关键词:
①“定义域I内某个区间D”,即函数的单调区间是其定义域的子集.单调性是与“区间”紧密相关的,一个函数在不同区间可以有不同的单调性;②“对于…”,“任意…”,“都有…”,“对于”即两个自变量x1,x2,必须取自给定的区间;“任意”即不能用特殊值代替;“都有”即只要x1<x2,就必须有f(x1)<f(x2)或f(x1)>f(x2).
(2)函数单调性的刻画:
①图形刻画,对于给定区间上的函数y=f(x),它的图象若从左向右连续上升(下降),则称函数在该区间上是单调递增(减)的;
②定性刻画,对于给定区间上的函数y=f(x),若函数值随自变量的增大而增大(减小),则称函数在该区间上是单调递增(减)的.2.判定函数单调性的常见方法
(1)定义法.这是证明或判定函数单调性的常用方法.
(2)图象法.
根据函数图象的升、降情况进行判断.
(3)直接法.
运用已知的结论,直接得到函数的单调性,如一次函数、二次函数、反比例函数的单调性均可直接说出.直接判断函数的单调性,可用到以下结论:
①函数y=-f(x)与函数y=f(x)的单调性相反.已知f(x)是定义在[-1,1]上的增函数,且f(x-2)<
f(1-x),求x的取值范围.【错因】 出现上述错误解法的原因主要为不清楚抽象函数的定义域,在抽象函数中满足函数关系式的自变量首先应在定义域内,这是一个极易被忽视也是极易出现错误的地方,也就是说变量x首先应满足-1≤x-2≤1,-1≤1-x≤1,在此基础上利用单调性的定义将“ f ”符号脱掉.课时作业
点击进入链接
1.定义域为Ⅰ的函数f(x)的增减性2.函数的单调区间
如果函数y=f(x)在区间D上是__________________,那么就说函数y=f(x)在这一区间上具有(严格的)单调性,区间D叫做y=f(x)的____________.增函数(或减函数)单调区间1.在增减函数定义中,能否把“任意两个自变量”改为“存在两个自变量”?
【提示】 不能.如图所示,虽然f(-1)
①函数解析式中含有根号;
②用定义证明.
解答本题只需按照函数单调递增的定义加以证明.证明函数单调性的常用方法是定义法或图象法,利用定义法判断函数单调性的步骤为:已知函数y=f(x)的图象如图所示,试根据图象研究函数的单调区间.【思路点拨】 结合图象―→确定单调区间
【解析】 函数的定义域为R,由图象可知,(-∞,-1)和[0,1)是这个函数的递增区间,[-1,0)和[1,+∞)是这个函数的递减区间.(1)利用图象研究函数的单调性是常用的解题方法.但要注意函数的定义域.
(2)写单调区间时,不连续的单调区间必须分开写,不能用“∪”符号连接它们.2.如图为函数y=f(x)的图象,根据图象写出函数的单调区间并判断在每一区间它是增函数还是减函数.【解析】 由函数y=f(x)的图象知单调区间有(-∞,-2),
[-2,1),[1,3)和[3,+∞).其中,在区间(-∞,-2)和[1,3)上函数f(x)为增函数;在区间[-2,1)和[3,+∞)上函数f(x)为减函数.已知函数f(x)=x2-2(a-1)x+3在区间(-∞,4]上是减函数,求实数a的取值范围.
【思路点拨】 由题目可获取以下主要信息:
①所给函数为二次函数,且含有参数;
②函数在区间(-∞,4]上是减函数.
解答本题可先将函数解析式配方,然后找出图象的对称轴,再考虑对称轴与所给区间的位置关系,利用数形结合求解.【解析】 f(x)=x2-2(a-1)x+3
=[x-(a-1)]2-(a-1)2+3,
∴此二次函数的对称轴为x=a-1.
∴f(x)的单调减区间为(-∞,a-1].
∵f(x)在(-∞,4]上是减函数,
∴对称轴x=a-1必须在直线x=4的右侧或与其重合.
∴a-1≥4,解得a≥5.(1)二次函数是常见函数,遇到二次函数后就配方找对称轴,画出图象,会给研究问题带来很大的方便.
(2)已知函数单调性求参数的取值范围,要注意数形结合,采用逆向思维方法.3.本例中,若将函数“在区间(-∞,4]上是减函数”改为“函数的单调递减区间为(-∞,4]”,则a为何值?
【解析】 由例题知函数f(x)的单调递减区间为(-∞,1-a],
∴a-1=4,a=5.1.解读函数单调性的定义
(1)定义中的关键词:
①“定义域I内某个区间D”,即函数的单调区间是其定义域的子集.单调性是与“区间”紧密相关的,一个函数在不同区间可以有不同的单调性;②“对于…”,“任意…”,“都有…”,“对于”即两个自变量x1,x2,必须取自给定的区间;“任意”即不能用特殊值代替;“都有”即只要x1<x2,就必须有f(x1)<f(x2)或f(x1)>f(x2).
(2)函数单调性的刻画:
①图形刻画,对于给定区间上的函数y=f(x),它的图象若从左向右连续上升(下降),则称函数在该区间上是单调递增(减)的;
②定性刻画,对于给定区间上的函数y=f(x),若函数值随自变量的增大而增大(减小),则称函数在该区间上是单调递增(减)的.2.判定函数单调性的常见方法
(1)定义法.这是证明或判定函数单调性的常用方法.
(2)图象法.
根据函数图象的升、降情况进行判断.
(3)直接法.
运用已知的结论,直接得到函数的单调性,如一次函数、二次函数、反比例函数的单调性均可直接说出.直接判断函数的单调性,可用到以下结论:
①函数y=-f(x)与函数y=f(x)的单调性相反.已知f(x)是定义在[-1,1]上的增函数,且f(x-2)<
f(1-x),求x的取值范围.【错因】 出现上述错误解法的原因主要为不清楚抽象函数的定义域,在抽象函数中满足函数关系式的自变量首先应在定义域内,这是一个极易被忽视也是极易出现错误的地方,也就是说变量x首先应满足-1≤x-2≤1,-1≤1-x≤1,在此基础上利用单调性的定义将“ f ”符号脱掉.课时作业
点击进入链接
