高一(人教a版)第二章数学课件:2.2.1对数与对数运算(第1课时对数)
文档属性
| 名称 | 高一(人教a版)第二章数学课件:2.2.1对数与对数运算(第1课时对数) |  | |
| 格式 | rar | ||
| 文件大小 | 736.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-01 16:56:00 | ||
图片预览








文档简介
课件23张PPT。2.2.1 对数与对数运算(第1课时 对数)
1.ax=N称作 式.其中a_____称作,x称作 ,ax称作: .指数底数指数幂1.alogaN=N成立吗?(a>0,a≠1,N>0)?为什么?
【提示】 成立.此式称为对数恒等式.设ab=N,则b=logaN,
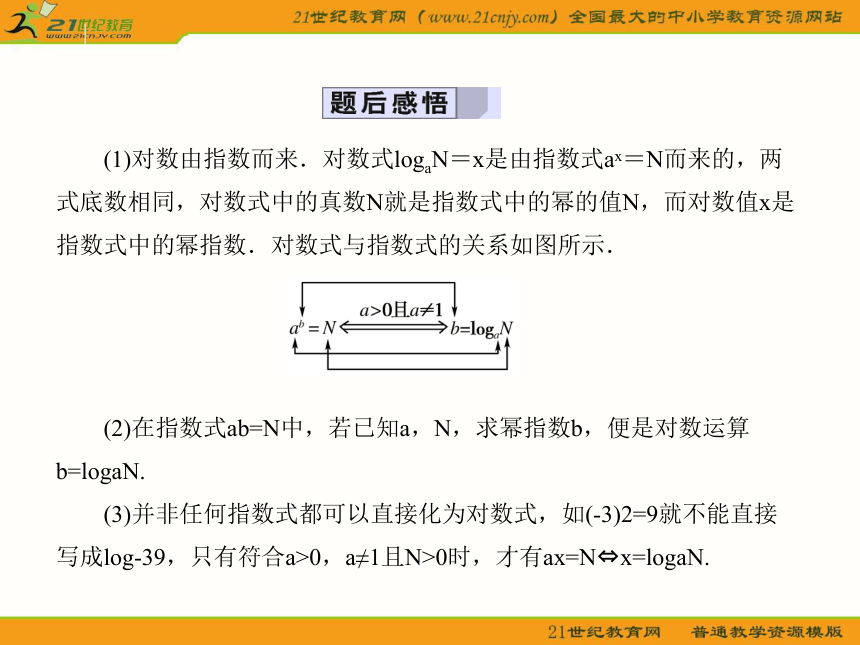
∴ab=alogaN=N.(1)对数由指数而来.对数式logaN=x是由指数式ax=N而来的,两式底数相同,对数式中的真数N就是指数式中的幂的值N,而对数值x是指数式中的幂指数.对数式与指数式的关系如图所示.
(2)在指数式ab=N中,若已知a,N,求幂指数b,便是对数运算b=logaN.
(3)并非任何指数式都可以直接化为对数式,如(-3)2=9就不能直接写成log-39,只有符合a>0,a≠1且N>0时,才有ax=N?x=logaN.有关“底数”和“1”的对数,可利用对数的性质求出其值“1”和“0”,化成常数,有利于化简和计算.求值:
(1)31+log35;(2)10lg3+lg4;(3)blogba·alogac
【思路点拨】 由题目可获取以下主要信息:
①指数中含有对数值.
②底数与指数式的底数相同.解答本题可使用对数恒等式
alogaN=N来化简求值.
【解析】 (1)原式=3·3log35=3·5=15.
(2)原式=10lg3·10lg4=3·4=12.
(3)原式=a·c要牢记对数恒等式,对于对数恒等式alogaN=N要注意格式:①它们是同底的;②指数中含有对数形式;③其值为对数的真数.
3.求值1.准确理解对数概念.
对数符号logaN只有在a>0,a≠1且N>0时才有意义,这是因为:
(1)若a<0,则N取某些数值时,x不存在,为此规定a不能小于0.2.准确认识指数式与对数式的关系
(1)在关系式ax=N中,已知a和x求N的运算称为求幂运算;而如果已知a和N,求x,就是对数运算.两个式子实质相同而形式不同,互为逆运算.
(2)并非任何指数式都可以直接化为对数式,如(-3)2=9就不能直接写成log-39,只有符合a>0,a≠1且N>0时,才有ax=N?x=logaN.求log(1-2x)(3x+2)中的x的取值范围.
【错解】 ∵对数的真数大于0,∴3x+2>0,
∴x>-2/3.
【错因】 本题错解的原因是忽视对数底数的限制范围.底数1-2x需大于零且不等于1.课时作业
点击进入链接页码以及子标题内容页
1.ax=N称作 式.其中a_____称作,x称作 ,ax称作: .指数底数指数幂1.alogaN=N成立吗?(a>0,a≠1,N>0)?为什么?
【提示】 成立.此式称为对数恒等式.设ab=N,则b=logaN,
∴ab=alogaN=N.(1)对数由指数而来.对数式logaN=x是由指数式ax=N而来的,两式底数相同,对数式中的真数N就是指数式中的幂的值N,而对数值x是指数式中的幂指数.对数式与指数式的关系如图所示.
(2)在指数式ab=N中,若已知a,N,求幂指数b,便是对数运算b=logaN.
(3)并非任何指数式都可以直接化为对数式,如(-3)2=9就不能直接写成log-39,只有符合a>0,a≠1且N>0时,才有ax=N?x=logaN.有关“底数”和“1”的对数,可利用对数的性质求出其值“1”和“0”,化成常数,有利于化简和计算.求值:
(1)31+log35;(2)10lg3+lg4;(3)blogba·alogac
【思路点拨】 由题目可获取以下主要信息:
①指数中含有对数值.
②底数与指数式的底数相同.解答本题可使用对数恒等式
alogaN=N来化简求值.
【解析】 (1)原式=3·3log35=3·5=15.
(2)原式=10lg3·10lg4=3·4=12.
(3)原式=a·c要牢记对数恒等式,对于对数恒等式alogaN=N要注意格式:①它们是同底的;②指数中含有对数形式;③其值为对数的真数.
3.求值1.准确理解对数概念.
对数符号logaN只有在a>0,a≠1且N>0时才有意义,这是因为:
(1)若a<0,则N取某些数值时,x不存在,为此规定a不能小于0.2.准确认识指数式与对数式的关系
(1)在关系式ax=N中,已知a和x求N的运算称为求幂运算;而如果已知a和N,求x,就是对数运算.两个式子实质相同而形式不同,互为逆运算.
(2)并非任何指数式都可以直接化为对数式,如(-3)2=9就不能直接写成log-39,只有符合a>0,a≠1且N>0时,才有ax=N?x=logaN.求log(1-2x)(3x+2)中的x的取值范围.
【错解】 ∵对数的真数大于0,∴3x+2>0,
∴x>-2/3.
【错因】 本题错解的原因是忽视对数底数的限制范围.底数1-2x需大于零且不等于1.课时作业
点击进入链接页码以及子标题内容页
