高一(人教a版)第二章数学课件:2.2.2对数函数及其性质(第1课时对数函数的图象及性质)
文档属性
| 名称 | 高一(人教a版)第二章数学课件:2.2.2对数函数及其性质(第1课时对数函数的图象及性质) |

|
|
| 格式 | rar | ||
| 文件大小 | 794.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-01 00:00:00 | ||
图片预览








文档简介
课件23张PPT。2.2.2 对数函数及其性质(第1课时 对数函数的图象及性质)
1.如果ax=N,(a>0且a≠1),那么数x叫做 ,记作x=logaN,a叫做 ,N叫做 .
2.a>0,且a≠1,M>0,N>0,那么以a为底N的对数底数真数1.对数函数的概念
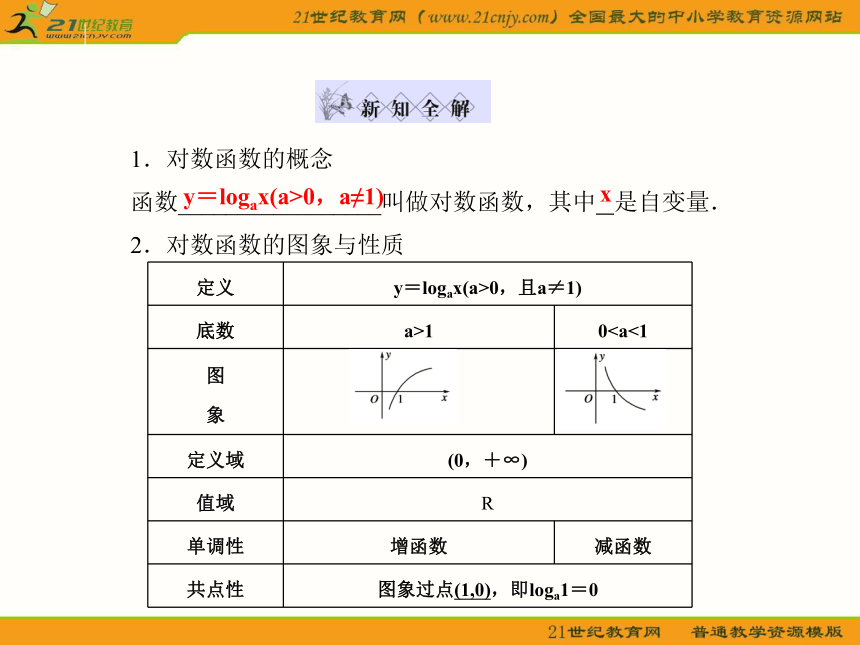
函数_________________叫做对数函数,其中 是自变量.
2.对数函数的图象与性质y=logax(a>0,a≠1)x 3.反函数
对数函数y=logax(a>0且a≠1)和_____________互为反函数.指数函数y=ax1.函数y=ax与y=logax的定义域与值域有什么关系.
【提示】 y=ax的定义域为R,值域为(0,+∞),y=logax的定义域为(0,+∞),值域为R,即它们的定义域和值域互换.
2.一个函数为对数函数的条件是什么?
【提示】 一个函数为对数函数的条件是:
①系数为1;
②底数为大于0且不等于1的正常数;
③自变量为真数.下列函数中,哪些是对数函数.
(1)y=log3(x+1);(2)y=5log2x;(3)y=log3x-1;(4)y=logxa(x>0且x≠1);(5)y=lg x;(6)y=ln x2.
【思路点拨】 由题目可获取以下主要信息:
①所给函数中有些形似对数函数的函数;
②此题主要考查对数函数的定义.
解答本题可根据对数函数的定义寻找其满足的条件.【解析】 (5)是对数函数;
(1)中真数不是自变量x,∴不是对数函数;(2)中log2x前的系数是5,而不是1,∴不是对数函数;
(3)中对数式后减1,∴不是对数函数;
(4)中底数是自变量x,而非常数a,∴不是对数函数;
(6)中真数是x2,不是自变量x,∴不是对数函数.一个函数为对数函数的条件是:
①系数为1;
②底数为大于0且不等于1的常数;
③真数为单个自变量x.
1.若函数f(x)=ax(a>0且a≠1)的反函数的图象过点(4,1),则a=________.
【解析】 y=ax的反函数为y=logax,
由题意知loga4=1,∴a=4.
【答案】 4求下列函数的定义域.求与对数函数有关的函数定义域时,除遵循前面已学习过的求函数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注意真数大于零;二是要注意对数的底数,三是按底数的取值应用单调性,有针对性的解不等式.A.向左平移3个单位长度,再向上平移1个单位长度
B.向右平移3个单位长度,再向上平移1个单位长度
C.向左平移3个单位长度,再向下平移1个单位长度
D.向右平移3个单位长度,再向下平移1个单位长度【思路点拨】 本题目可以获取以下主要信息:
①函数y=lg x通过平移变换得到y=f(x)图象;
②f(x)=lg(x+3)-1.
解决本类问题利用图象变换作图即可.(1)一般地,函数y=f(x±a)±b(a、b为正数)的图象可由函数y=f(x)的图象变换得到.
将y=f(x)的图象向左或向右平移a个单位可得到函数
y=f(x±a)的图象,向下或向上平移b个单位可得到函数y=f(x±a)±b的图象(记忆口诀:左加右减,上加下减).
(2)含有绝对值的函数的图象变换是一种对称变换,一般地,y=f(|x-a|)的图象是关于x=a对称的轴对称图形;函数y=
|f(x)|的图象与y=f(x)的图象在x轴上方相同,在x轴下方关于x轴对称.
(3)y=f(x)的图象与y=f(-x)的图象关于y轴对称,y=f(x)的图象与y=-f(x)的图象关于x轴对称.3.已知a>0且a≠1,函数y=ax与y=loga(-x)的图象可能是( )
【解析】 由y=loga(-x)的定义域为(-∞,0)知,图象应在y轴左侧,可排除A、D选项.
当a>1时,y=ax应为增函数,y=loga(-x)应为减函数,可知B项正确.
而对C项,由图象知y=ax递减?0【答案】 B1.对对数函数定义的理解
(1)同指数函数一样,对数函数仍然采用形式定义,如y=2log2x,y=log2x2等都不是对数函数,只有y=logax(a>0,且a≠1)才是.
(2)由于指数函数y=ax(a>0,且a≠1)的定义域是R,值域为(0,+∞),再根据对数式与指数式的互化过程知道对数函数y=logax(a>0,且a≠1)的定义域为(0,+∞),值域为
(-∞,+∞),它们互为反函数.2.函数y=logax(a>0且a≠1)的底数变化对图象位置的影响
观察图象,注意变化规律:
(1)上下比较:在直线x=1的右侧,a>1时,a越大,图象越靠近x轴,0(2)左右比较:(比较图象与y=1的交点)交点的横坐标越大,对应的对数函数的底数越大.画对数函数y=logax的图象时,应抓住三个关键点(a,1),(1,0),(1/a,-1).
已知函数y=f(x),x,y满足关系式lg(lg y)=lg(3x)+
lg(3-x),求函数y=f(x)的表达式及定义域,值域.
【错解】 因为lg(lg y)=lg(3x)+lg(3-x)
=lg[3x(3-x)] ①,
所以lg y=3x(3-x),所以y=103x(3-x)(x∈R,y>0).课时作业
点击进入链接页码以及子标题内容页
1.如果ax=N,(a>0且a≠1),那么数x叫做 ,记作x=logaN,a叫做 ,N叫做 .
2.a>0,且a≠1,M>0,N>0,那么以a为底N的对数底数真数1.对数函数的概念
函数_________________叫做对数函数,其中 是自变量.
2.对数函数的图象与性质y=logax(a>0,a≠1)x 3.反函数
对数函数y=logax(a>0且a≠1)和_____________互为反函数.指数函数y=ax1.函数y=ax与y=logax的定义域与值域有什么关系.
【提示】 y=ax的定义域为R,值域为(0,+∞),y=logax的定义域为(0,+∞),值域为R,即它们的定义域和值域互换.
2.一个函数为对数函数的条件是什么?
【提示】 一个函数为对数函数的条件是:
①系数为1;
②底数为大于0且不等于1的正常数;
③自变量为真数.下列函数中,哪些是对数函数.
(1)y=log3(x+1);(2)y=5log2x;(3)y=log3x-1;(4)y=logxa(x>0且x≠1);(5)y=lg x;(6)y=ln x2.
【思路点拨】 由题目可获取以下主要信息:
①所给函数中有些形似对数函数的函数;
②此题主要考查对数函数的定义.
解答本题可根据对数函数的定义寻找其满足的条件.【解析】 (5)是对数函数;
(1)中真数不是自变量x,∴不是对数函数;(2)中log2x前的系数是5,而不是1,∴不是对数函数;
(3)中对数式后减1,∴不是对数函数;
(4)中底数是自变量x,而非常数a,∴不是对数函数;
(6)中真数是x2,不是自变量x,∴不是对数函数.一个函数为对数函数的条件是:
①系数为1;
②底数为大于0且不等于1的常数;
③真数为单个自变量x.
1.若函数f(x)=ax(a>0且a≠1)的反函数的图象过点(4,1),则a=________.
【解析】 y=ax的反函数为y=logax,
由题意知loga4=1,∴a=4.
【答案】 4求下列函数的定义域.求与对数函数有关的函数定义域时,除遵循前面已学习过的求函数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注意真数大于零;二是要注意对数的底数,三是按底数的取值应用单调性,有针对性的解不等式.A.向左平移3个单位长度,再向上平移1个单位长度
B.向右平移3个单位长度,再向上平移1个单位长度
C.向左平移3个单位长度,再向下平移1个单位长度
D.向右平移3个单位长度,再向下平移1个单位长度【思路点拨】 本题目可以获取以下主要信息:
①函数y=lg x通过平移变换得到y=f(x)图象;
②f(x)=lg(x+3)-1.
解决本类问题利用图象变换作图即可.(1)一般地,函数y=f(x±a)±b(a、b为正数)的图象可由函数y=f(x)的图象变换得到.
将y=f(x)的图象向左或向右平移a个单位可得到函数
y=f(x±a)的图象,向下或向上平移b个单位可得到函数y=f(x±a)±b的图象(记忆口诀:左加右减,上加下减).
(2)含有绝对值的函数的图象变换是一种对称变换,一般地,y=f(|x-a|)的图象是关于x=a对称的轴对称图形;函数y=
|f(x)|的图象与y=f(x)的图象在x轴上方相同,在x轴下方关于x轴对称.
(3)y=f(x)的图象与y=f(-x)的图象关于y轴对称,y=f(x)的图象与y=-f(x)的图象关于x轴对称.3.已知a>0且a≠1,函数y=ax与y=loga(-x)的图象可能是( )
【解析】 由y=loga(-x)的定义域为(-∞,0)知,图象应在y轴左侧,可排除A、D选项.
当a>1时,y=ax应为增函数,y=loga(-x)应为减函数,可知B项正确.
而对C项,由图象知y=ax递减?0
(1)同指数函数一样,对数函数仍然采用形式定义,如y=2log2x,y=log2x2等都不是对数函数,只有y=logax(a>0,且a≠1)才是.
(2)由于指数函数y=ax(a>0,且a≠1)的定义域是R,值域为(0,+∞),再根据对数式与指数式的互化过程知道对数函数y=logax(a>0,且a≠1)的定义域为(0,+∞),值域为
(-∞,+∞),它们互为反函数.2.函数y=logax(a>0且a≠1)的底数变化对图象位置的影响
观察图象,注意变化规律:
(1)上下比较:在直线x=1的右侧,a>1时,a越大,图象越靠近x轴,0
已知函数y=f(x),x,y满足关系式lg(lg y)=lg(3x)+
lg(3-x),求函数y=f(x)的表达式及定义域,值域.
【错解】 因为lg(lg y)=lg(3x)+lg(3-x)
=lg[3x(3-x)] ①,
所以lg y=3x(3-x),所以y=103x(3-x)(x∈R,y>0).课时作业
点击进入链接页码以及子标题内容页
