高一(人教a版)第二章数学课件:2.3幂函数
文档属性
| 名称 | 高一(人教a版)第二章数学课件:2.3幂函数 |

|
|
| 格式 | rar | ||
| 文件大小 | 701.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-01 00:00:00 | ||
图片预览








文档简介
课件22张PPT。2.3 幂函数
1.形如 是指数函数,定义域R,值域 .
2.形如y=logax是对数函数,定义域 ,值域R.(0,+∞)y=ax(0,+∞)1.幂函数的概念
函数 叫做幂函数,其中 是自变量, 是常数.
2.幂函数的图象
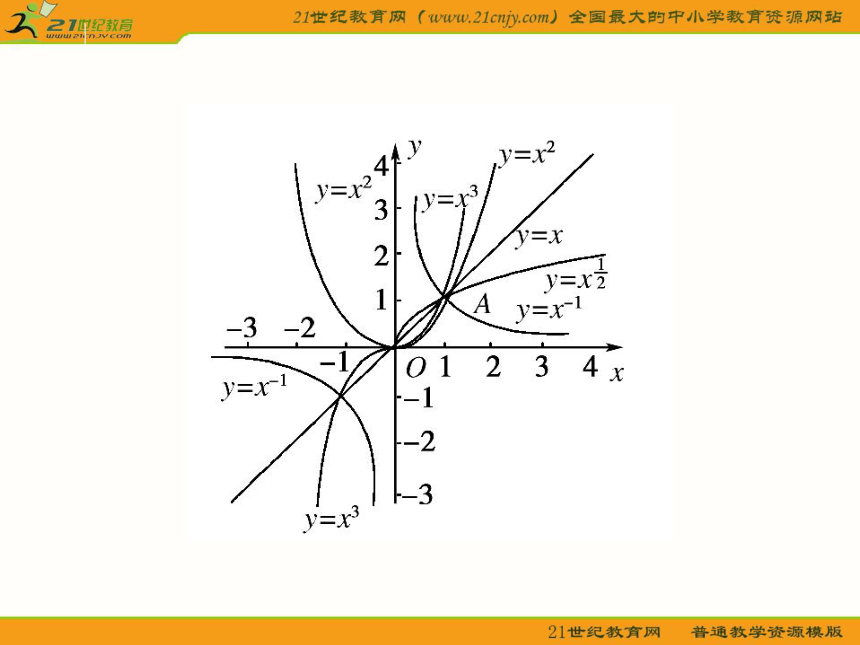
在同一坐标系中,幂函数y=x,y=x2,y=x3,y=x1/2,y=x-1的图象如图.y=xαxα3.幂函数的图象与性质
1.幂函数的图象能过第四象限吗?
【提示】 对幂函数y=xα而言,当x>0时,必有y>0,故幂函数图象不过第四象限.当x∈(0,+∞)时,幂函数y=(m2-m-1)x2m-1为增函数,求实数m的值.
【思路点拨】 由题目可获取以下主要信息:
①f(x)=(m2-m-1)x2m-1是幂函数;
②当x>0时,f(x)是增函数.
解答本题可严格根据幂函数的定义形式列方程求出m,再由单调性确定m.
【解析】 ∵函数y=(m2-m-1)x2m-1为幂函数,
∴m2-m-1=1,解得m=2或m=-1.
又∵函数f(x)在(0,+∞)上为增函数,
∴2m-1>0,即m>1/2,
故m=-1,舍去,∴m=2.幂函数y=xα(α∈R),其中α为常数,其本质特征是以幂的底x为自变量,指数α为常数(也可以为0).这是判断一个函数是否为幂函数的重要依据和唯一标准.对本例来说,还要根据单调性验根,以免增根.1.本例中将条件“增函数”改为“减函数”,求m的值.
【解析】 若函数f(x)为(0,+∞)上的减函数
则2m-1<0,∴m<1/2,
故m=2,舍去,∴m=-1. (1)求定义域;
(2)判断奇偶性;
(3)已知该函数在第一象限的图象如图所示,试补全图象,并由图象确定单调区间.
【思路点拨】 由题目可以获取以下信息:
函数解析式―→函数有意义(1)在研究幂函数的定义域时,通常将分数指数幂化为根式形式,负整数指数幂化为分式形式,然后由根式、分式有意义求定义域;
(2)画幂函数图象可先画出第一象限的部分,再由定义域、单调性、奇偶性得出其他象限的图象.2.已知幂函数y=f(x)的图象经过点(4,2),试求函数的解析式,并说明函数的单调性.
【解析】 由幂函数的概念设f(x)=xα,则由4α=2得α=1/2,故函数解析式为f(x)=x1/2 (x≥0),在[0,+∞)上是增函数.若(3-2m)1/2 >(m+1)1/2,求实数m的取值范围.
【思路点拨】 由题目可以获取以下主要信息:
①所给不等式两边幂指数相同;
②可以确定幂函数的单调性.
解答本题可以利用已知条件列出不等式组求出字母m的取值范围.利用函数的单调性时一定要注意函数的定义域.本题若没有注意到幂函数y=x1/2的定义域为[0,+∞),求解时就会得出m<2/3这一错误结果.1.幂函数的性质
(1)所有的幂函数在(0,+∞)上都有定义,并且图象都通过点(1,1),幂函数图象不过第四象限.
(2)α>0时,①幂函数的图象都通过点(0,0)(1,1);②并且在[0,+∞)上都是增函数.
(3)α<0时,①幂函数的图象都通过点(1,1);
②在[0,+∞)上都是减函数;
③在第一象限内,函数图象向上与y轴无限接近,向右与x轴无限接近.
幂函数在第一象限内指数变化规律:
在第一象限内直线x=1的右侧,图象从上到下,相应的指数由大变小;在直线x=1的左侧,图象从下到上,相应的指数由大变小.已知x2>x1/3,求x的取值范围.
【错解】 由于x2≥0,x1/3∈R,则由x2>x1/3,可得x∈R.
【错因】 上述错解原因是没有掌握幂函数的图象特征,尤其是y=xα在α>1和0<α<1两种情况下图象的分布.
【正解】 作出函数y=x2和y=x1/3的图象(如图所示),易得x<0或x>1.课时作业
点击进入链接
1.形如 是指数函数,定义域R,值域 .
2.形如y=logax是对数函数,定义域 ,值域R.(0,+∞)y=ax(0,+∞)1.幂函数的概念
函数 叫做幂函数,其中 是自变量, 是常数.
2.幂函数的图象
在同一坐标系中,幂函数y=x,y=x2,y=x3,y=x1/2,y=x-1的图象如图.y=xαxα3.幂函数的图象与性质
1.幂函数的图象能过第四象限吗?
【提示】 对幂函数y=xα而言,当x>0时,必有y>0,故幂函数图象不过第四象限.当x∈(0,+∞)时,幂函数y=(m2-m-1)x2m-1为增函数,求实数m的值.
【思路点拨】 由题目可获取以下主要信息:
①f(x)=(m2-m-1)x2m-1是幂函数;
②当x>0时,f(x)是增函数.
解答本题可严格根据幂函数的定义形式列方程求出m,再由单调性确定m.
【解析】 ∵函数y=(m2-m-1)x2m-1为幂函数,
∴m2-m-1=1,解得m=2或m=-1.
又∵函数f(x)在(0,+∞)上为增函数,
∴2m-1>0,即m>1/2,
故m=-1,舍去,∴m=2.幂函数y=xα(α∈R),其中α为常数,其本质特征是以幂的底x为自变量,指数α为常数(也可以为0).这是判断一个函数是否为幂函数的重要依据和唯一标准.对本例来说,还要根据单调性验根,以免增根.1.本例中将条件“增函数”改为“减函数”,求m的值.
【解析】 若函数f(x)为(0,+∞)上的减函数
则2m-1<0,∴m<1/2,
故m=2,舍去,∴m=-1. (1)求定义域;
(2)判断奇偶性;
(3)已知该函数在第一象限的图象如图所示,试补全图象,并由图象确定单调区间.
【思路点拨】 由题目可以获取以下信息:
函数解析式―→函数有意义(1)在研究幂函数的定义域时,通常将分数指数幂化为根式形式,负整数指数幂化为分式形式,然后由根式、分式有意义求定义域;
(2)画幂函数图象可先画出第一象限的部分,再由定义域、单调性、奇偶性得出其他象限的图象.2.已知幂函数y=f(x)的图象经过点(4,2),试求函数的解析式,并说明函数的单调性.
【解析】 由幂函数的概念设f(x)=xα,则由4α=2得α=1/2,故函数解析式为f(x)=x1/2 (x≥0),在[0,+∞)上是增函数.若(3-2m)1/2 >(m+1)1/2,求实数m的取值范围.
【思路点拨】 由题目可以获取以下主要信息:
①所给不等式两边幂指数相同;
②可以确定幂函数的单调性.
解答本题可以利用已知条件列出不等式组求出字母m的取值范围.利用函数的单调性时一定要注意函数的定义域.本题若没有注意到幂函数y=x1/2的定义域为[0,+∞),求解时就会得出m<2/3这一错误结果.1.幂函数的性质
(1)所有的幂函数在(0,+∞)上都有定义,并且图象都通过点(1,1),幂函数图象不过第四象限.
(2)α>0时,①幂函数的图象都通过点(0,0)(1,1);②并且在[0,+∞)上都是增函数.
(3)α<0时,①幂函数的图象都通过点(1,1);
②在[0,+∞)上都是减函数;
③在第一象限内,函数图象向上与y轴无限接近,向右与x轴无限接近.
幂函数在第一象限内指数变化规律:
在第一象限内直线x=1的右侧,图象从上到下,相应的指数由大变小;在直线x=1的左侧,图象从下到上,相应的指数由大变小.已知x2>x1/3,求x的取值范围.
【错解】 由于x2≥0,x1/3∈R,则由x2>x1/3,可得x∈R.
【错因】 上述错解原因是没有掌握幂函数的图象特征,尤其是y=xα在α>1和0<α<1两种情况下图象的分布.
【正解】 作出函数y=x2和y=x1/3的图象(如图所示),易得x<0或x>1.课时作业
点击进入链接
