12.2实数与数轴
图片预览
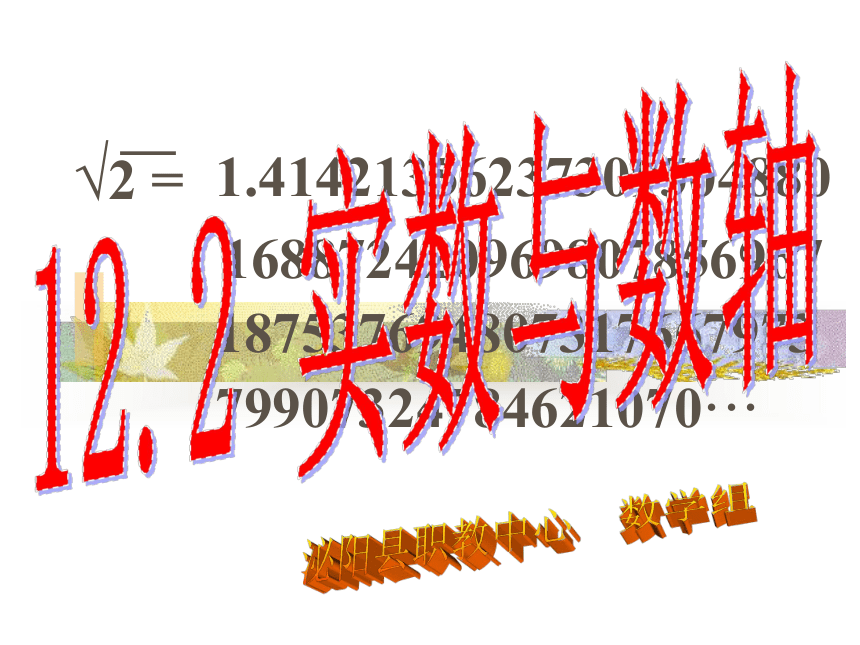





文档简介
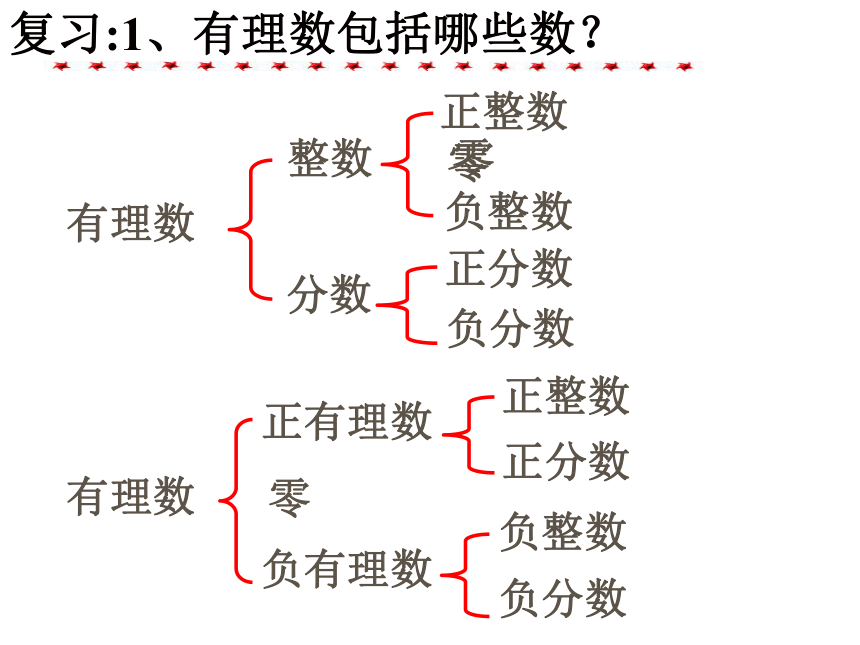
课件26张PPT。1.41421356237309504880 168872420969807856967 187537694807317667973 79907324784621070··· 12.2 实数与数轴 泌阳县职教中心 数学组复习:1、有理数包括哪些数?有理数整数分数正整数 零负整数正分数负分数有理数正有理数零负有理数正整数正分数负整数负分数零2、有理数中的分数能化为小数吗?
化为什么样的小数?举例加以说明
答:任何一个分数可写成小数的形式,必是
有限小数或者无限循环小数 例如结果约为:1.4142135623730950488016887242096980785696718753769480731766797379907324784621070388503875343276415727350138462309122970249248360558507372126441214970999358314132226659275055927557999505011527820605715……问题2:你能利用平方关系验算得到的结果吗?问题1中的结果平方后会等于2吗?做一做 问题3:验证的结果不是2,而是接近2, 这说明什么?做一做 结果为:1.4142135623730950488016887242096980785696718753769480731766797379907324784621070388503875343276415727350138462309122970249248360558507372126441214970999358314132226659275055927557999505011527820605715……问题4:后面能否写完?后面有没有规律?那么它属于什么小数?在数学上已经证明,没有一个有理数(即整数或分数)的平方等于2,也就是说,
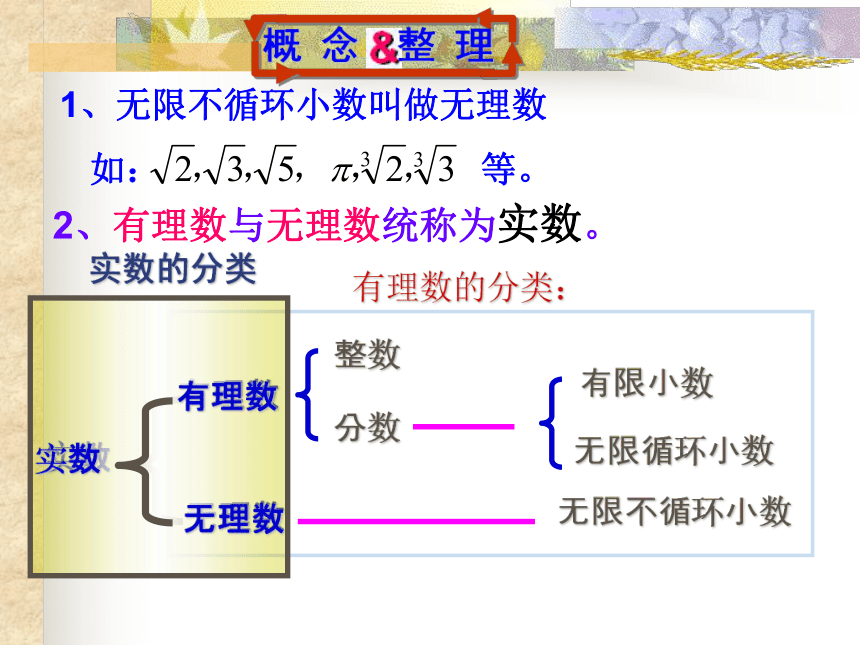
不是一个有理数. 无理数:
无限不循环小数叫做无理数。有理数整数分数有限小数无限循环小数无理数无限不循环小数实数实数的分类1、无限不循环小数叫做无理数
如: 等。2、有理数与无理数统称为实数。
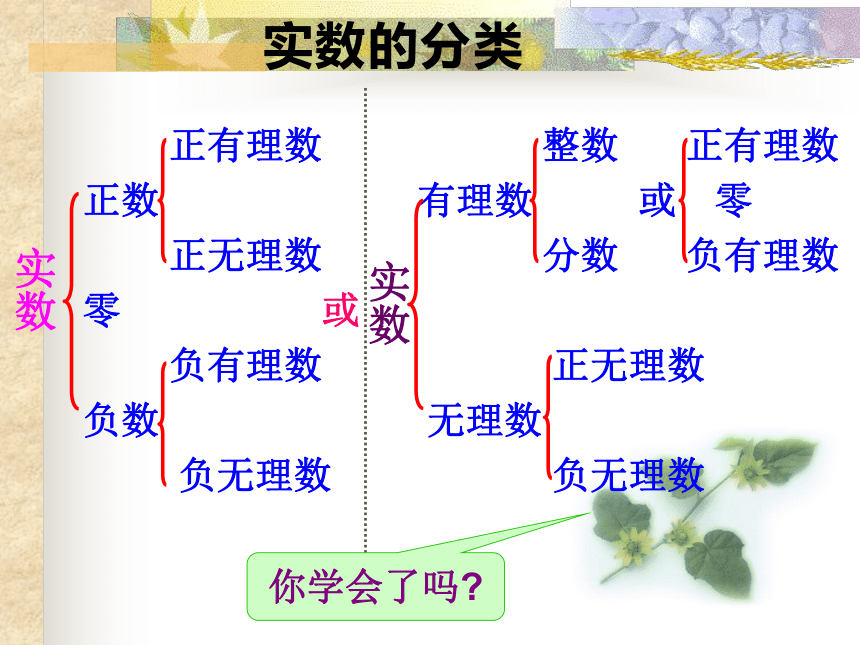
正有理数 整数 正有理数
正数 有理数 或 零
正无理数 分数 负有理数
零 或
负有理数 正无理数
负数 无理数
负无理数 负无理数实数的分类你学会了吗?实数实数注意:(2)无理数不一定都是用根号表示的数.如:π (3)无理数有无数多个.(4)无理数可分为正无理数和负无理数.(1)用根号表示的数不一定是无理数.如:巩固 练 习巩固 把下列各数分别填入相应的括号内: ,,,,,,,,,,。 把下列各数分别填入相应的括号内: 练一练把下列各数填入相应的集合内:如图是两个边长1的正方形操作探索拼成的长方形, 其面积是2. 现剪下两个角重新拼成一个 正方形, 新正方形的边长是_____ 下图数轴中, 正方形的对角线长为____, 以原点为圆心, 对角线长为半径画弧截得一点, 该点与原点的距离是____, 该点表示的数是____. 实数与数轴上的点是一一对应关系.我们也可以这样来思考:11正方形的面积为2
实数与数轴上的点的对应每一个实数都可以用数轴上的一个点来表示。反过来 ,数轴上的每一个点都表示一个实数。(数?点)(点?数)一一对应实数范围内的相关概念在实数范围内 ,相反数、倒数、绝对值的意义 ,和有理数范围内 的相反数、倒数、绝对值的意义 ,完全一样。例如:正实数的大小比较和运算,
通常可取它们的近似值来进行 解:用计算器求得 而所以 解:用计算器求得 ≈-0.778 539 072, 于是 ≈0.778 539 072, 所以 ≈1.570 796 327-0.778 539 072=0.792 257 255≈0.79练 习
1.判断下列说法是否正确:
(1)两个数相除,如果不管添多少位小数,永远都除不尽,那么结果一定是一个无理数
(2)任意一个无理数的绝对值是正数.
2.计算: .(结果保留两位小数)
3.比较下列各组数中两个实数的大小:
(1) (2) 一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.无理数都是开方开不尽的数。( )7. 无理数包括正无理数、零、负无理数。( )9.数轴上的任何一点都可以表示实数。( )×××8.有理数都是有限小数。( )××二、填空5、在实数 中,
整数有
有理数有
无理数有
实数有它本身0它的相反数思维拓展回顾小结1、无理数与实数:2、实数与数轴:每个实数都能在数轴上找到一个对应的点, 无理数的运算适用于有理数的一切运算法则.无理数与有理数统称为实数. 无限不循环小数叫做无理数. 反之, 数轴上每一个点都对应一个实数. (一一对应) 3、无理数的运算:
正有理数 整数 正有理数
正数 有理数 或 零
正无理数 分数 负有理数
零 或
负有理数 正无理数
负数 无理数
负无理数 负无理数实数的分类实数实数作 业: P14 A组题再见!
化为什么样的小数?举例加以说明
答:任何一个分数可写成小数的形式,必是
有限小数或者无限循环小数 例如结果约为:1.4142135623730950488016887242096980785696718753769480731766797379907324784621070388503875343276415727350138462309122970249248360558507372126441214970999358314132226659275055927557999505011527820605715……问题2:你能利用平方关系验算得到的结果吗?问题1中的结果平方后会等于2吗?做一做 问题3:验证的结果不是2,而是接近2, 这说明什么?做一做 结果为:1.4142135623730950488016887242096980785696718753769480731766797379907324784621070388503875343276415727350138462309122970249248360558507372126441214970999358314132226659275055927557999505011527820605715……问题4:后面能否写完?后面有没有规律?那么它属于什么小数?在数学上已经证明,没有一个有理数(即整数或分数)的平方等于2,也就是说,
不是一个有理数. 无理数:
无限不循环小数叫做无理数。有理数整数分数有限小数无限循环小数无理数无限不循环小数实数实数的分类1、无限不循环小数叫做无理数
如: 等。2、有理数与无理数统称为实数。
正有理数 整数 正有理数
正数 有理数 或 零
正无理数 分数 负有理数
零 或
负有理数 正无理数
负数 无理数
负无理数 负无理数实数的分类你学会了吗?实数实数注意:(2)无理数不一定都是用根号表示的数.如:π (3)无理数有无数多个.(4)无理数可分为正无理数和负无理数.(1)用根号表示的数不一定是无理数.如:巩固 练 习巩固 把下列各数分别填入相应的括号内: ,,,,,,,,,,。 把下列各数分别填入相应的括号内: 练一练把下列各数填入相应的集合内:如图是两个边长1的正方形操作探索拼成的长方形, 其面积是2. 现剪下两个角重新拼成一个 正方形, 新正方形的边长是_____ 下图数轴中, 正方形的对角线长为____, 以原点为圆心, 对角线长为半径画弧截得一点, 该点与原点的距离是____, 该点表示的数是____. 实数与数轴上的点是一一对应关系.我们也可以这样来思考:11正方形的面积为2
实数与数轴上的点的对应每一个实数都可以用数轴上的一个点来表示。反过来 ,数轴上的每一个点都表示一个实数。(数?点)(点?数)一一对应实数范围内的相关概念在实数范围内 ,相反数、倒数、绝对值的意义 ,和有理数范围内 的相反数、倒数、绝对值的意义 ,完全一样。例如:正实数的大小比较和运算,
通常可取它们的近似值来进行 解:用计算器求得 而所以 解:用计算器求得 ≈-0.778 539 072, 于是 ≈0.778 539 072, 所以 ≈1.570 796 327-0.778 539 072=0.792 257 255≈0.79练 习
1.判断下列说法是否正确:
(1)两个数相除,如果不管添多少位小数,永远都除不尽,那么结果一定是一个无理数
(2)任意一个无理数的绝对值是正数.
2.计算: .(结果保留两位小数)
3.比较下列各组数中两个实数的大小:
(1) (2) 一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.无理数都是开方开不尽的数。( )7. 无理数包括正无理数、零、负无理数。( )9.数轴上的任何一点都可以表示实数。( )×××8.有理数都是有限小数。( )××二、填空5、在实数 中,
整数有
有理数有
无理数有
实数有它本身0它的相反数思维拓展回顾小结1、无理数与实数:2、实数与数轴:每个实数都能在数轴上找到一个对应的点, 无理数的运算适用于有理数的一切运算法则.无理数与有理数统称为实数. 无限不循环小数叫做无理数. 反之, 数轴上每一个点都对应一个实数. (一一对应) 3、无理数的运算:
正有理数 整数 正有理数
正数 有理数 或 零
正无理数 分数 负有理数
零 或
负有理数 正无理数
负数 无理数
负无理数 负无理数实数的分类实数实数作 业: P14 A组题再见!
