1.1.3集合的基本运算
图片预览








文档简介
课件21张PPT。1.1.3集合的
基本运算新课示例1:观察下列各组集合A={1,3,5}C={1,2,3,4,5,6}B={2,4,6} 集合C是由集合A或属于集合B的 元素组成的,则称C是A与B的并集.1.并 集定义:由所有属于集合A或B的元素组成
的集合,称为集合A与集合B的并集,记
作A∪B,即A∪B={x|x∈A或x∈B}.AB用Venn图表示为:ABABAB例1设集合A={4,5,6,8},
集合B={3,5,7,8,9},
求A∪B.A∪B={3,4,5,6,7,8,9}.A∪B={x|-1<x<3}.例2设集合A={x |-1<x<2},
集合B={x | 1<x<3},
求A∪B.x-1123①A∪A= ;
②A∪?= ;
③A∪B= .B∪AAA性质:示例2:考察下列各集合A={4,3,5};B={2,4,6};C={4}.2.交 集 集合C的元素既属于A,又属于B,
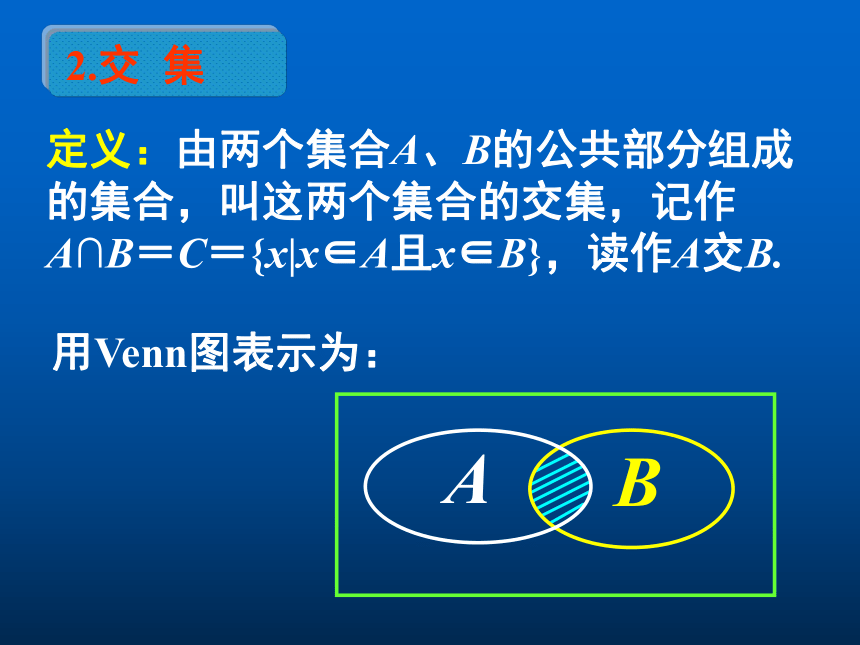
则称C为A与B的交集.2.交 集用Venn图表示为:定义:由两个集合A、B的公共部分组成
的集合,叫这两个集合的交集,记作
A∩B=C={x|x∈A且x∈B},读作A交B.AB例4⑴ A={2,4,6,8,10},
B={3,5,8,12},
C={6,8},
求①A∩B ②A∩(B∩C) ;⑵ A={x |x是某班参加百米赛的同学},
B={x |x是某班参加跳高的同学},
求A∩B.例5设集合A={y|y=x2,x∈R},
B={(x, y)|y=x+2,x∈R},
则A∩B =( )A.{(-1, 1),(2, 4)} B. {(-1, 1)}
C {(2, 4)} D. ?例5设集合A={y|y=x2,x∈R},
B={(x, y)|y=x+2,x∈R},
则A∩B =( )A.{(-1, 1),(2, 4)} B. {(-1, 1)}
C {(2, 4)} D. ?D①A∩B={x|x∈A且x∈B};
②A∩?=?,
A∩B=B∩A.性质:在实数范围内有三个解2,即:B={x∈R|(x-2)(x2-3)=0}={2, }。 在不同范围研究同一个问题,可能有不同的结果。(三)、全集与补集 如方程(x-2)(x2-3)=0的解集在有理数范围内只有一个解,即A={x∈Q|(x-2)(x2-3)=0}={2}, 定 义全集常用U表示. 如果一个集合含有我们所要研究的各个集合的全部元素,就称这个集合为全集(universe set)定 义对于一个集合A,由全集U中不属于A的所有元素组成的集合称为集合A相对于全集U的补集(complementary set),简称为集合A的补集,记作 UA例1 设U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},求CUA, CUB例2.设U={x|x是三角形},A={x|x是锐角三角形},B={x|x是钝角三角形}.求A∩B, CU (A∪B) 例3.已知全集U=R,集合A={x|1≤2x+1<9},求CUA 课堂小结⑴ A∪B={x|x∈A或x∈B},
A∩B={x|x∈A且x∈B};
② A∩A=A,A∪A=A,
A∩?=?,A∪?=A;
③ A∩B=B∩A,A∪B=B∪A.1.交集,并集2.性质3.全集 补集课堂练习教材P.11练习教材P.12习题1.1A组,B组课后作业教材P.12习题1.1A组第6、7、10题课时详解:P11 再 见
基本运算新课示例1:观察下列各组集合A={1,3,5}C={1,2,3,4,5,6}B={2,4,6} 集合C是由集合A或属于集合B的 元素组成的,则称C是A与B的并集.1.并 集定义:由所有属于集合A或B的元素组成
的集合,称为集合A与集合B的并集,记
作A∪B,即A∪B={x|x∈A或x∈B}.AB用Venn图表示为:ABABAB例1设集合A={4,5,6,8},
集合B={3,5,7,8,9},
求A∪B.A∪B={3,4,5,6,7,8,9}.A∪B={x|-1<x<3}.例2设集合A={x |-1<x<2},
集合B={x | 1<x<3},
求A∪B.x-1123①A∪A= ;
②A∪?= ;
③A∪B= .B∪AAA性质:示例2:考察下列各集合A={4,3,5};B={2,4,6};C={4}.2.交 集 集合C的元素既属于A,又属于B,
则称C为A与B的交集.2.交 集用Venn图表示为:定义:由两个集合A、B的公共部分组成
的集合,叫这两个集合的交集,记作
A∩B=C={x|x∈A且x∈B},读作A交B.AB例4⑴ A={2,4,6,8,10},
B={3,5,8,12},
C={6,8},
求①A∩B ②A∩(B∩C) ;⑵ A={x |x是某班参加百米赛的同学},
B={x |x是某班参加跳高的同学},
求A∩B.例5设集合A={y|y=x2,x∈R},
B={(x, y)|y=x+2,x∈R},
则A∩B =( )A.{(-1, 1),(2, 4)} B. {(-1, 1)}
C {(2, 4)} D. ?例5设集合A={y|y=x2,x∈R},
B={(x, y)|y=x+2,x∈R},
则A∩B =( )A.{(-1, 1),(2, 4)} B. {(-1, 1)}
C {(2, 4)} D. ?D①A∩B={x|x∈A且x∈B};
②A∩?=?,
A∩B=B∩A.性质:在实数范围内有三个解2,即:B={x∈R|(x-2)(x2-3)=0}={2, }。 在不同范围研究同一个问题,可能有不同的结果。(三)、全集与补集 如方程(x-2)(x2-3)=0的解集在有理数范围内只有一个解,即A={x∈Q|(x-2)(x2-3)=0}={2}, 定 义全集常用U表示. 如果一个集合含有我们所要研究的各个集合的全部元素,就称这个集合为全集(universe set)定 义对于一个集合A,由全集U中不属于A的所有元素组成的集合称为集合A相对于全集U的补集(complementary set),简称为集合A的补集,记作 UA例1 设U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},求CUA, CUB例2.设U={x|x是三角形},A={x|x是锐角三角形},B={x|x是钝角三角形}.求A∩B, CU (A∪B) 例3.已知全集U=R,集合A={x|1≤2x+1<9},求CUA 课堂小结⑴ A∪B={x|x∈A或x∈B},
A∩B={x|x∈A且x∈B};
② A∩A=A,A∪A=A,
A∩?=?,A∪?=A;
③ A∩B=B∩A,A∪B=B∪A.1.交集,并集2.性质3.全集 补集课堂练习教材P.11练习教材P.12习题1.1A组,B组课后作业教材P.12习题1.1A组第6、7、10题课时详解:P11 再 见
