3.3 相似三角形的性质和判定（4）

课件20张PPT。3.3 相似三角形的性质和判定
第4课时 相似三角形的性质、判定的综合运用湖南省新邵县酿溪中学王军旗学习目标1、系统掌握相似三角形的性质和判定定理。
2、会利用相似三角形的性质及判定定理解决
有关问题。1、什么叫相似三角形？ 三条边对应成比例，三个角对应相等的两个三角形叫相似三角形。
复习提问2、相似三角形有什么性质？ 相似三角形的对应边成比例，对应角相等。周长
的比等于相似比、对应高的比等于相似比，面积的
比等于像是比的平方。3、相似三角形有哪些判定方法？（1）三边对应成比例的两个三角形相似。
（2）有两个角对应相等的两个三角相似。
（3）有两边对应成比例，且夹角对应相等的两个三角形相似。
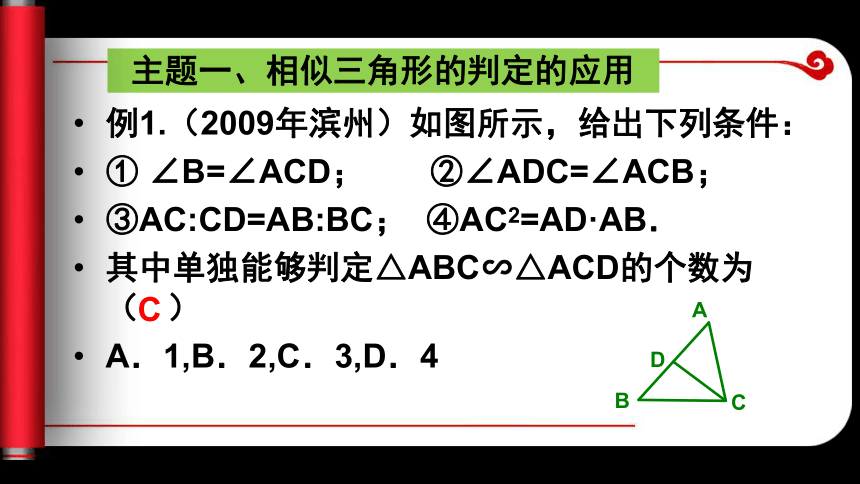
（4）斜边和一直角边对应成比例的两个直角三角形相似。主题一、相似三角形的判定的应用例1.（2009年滨州）如图所示，给出下列条件：
① ∠B=∠ACD； ②∠ADC=∠ACB；
③AC:CD=AB:BC； ④AC2=AD·AB．
其中单独能够判定△ABC∽△ACD的个数为（ ）
A．1,B．2,C．3,D．4
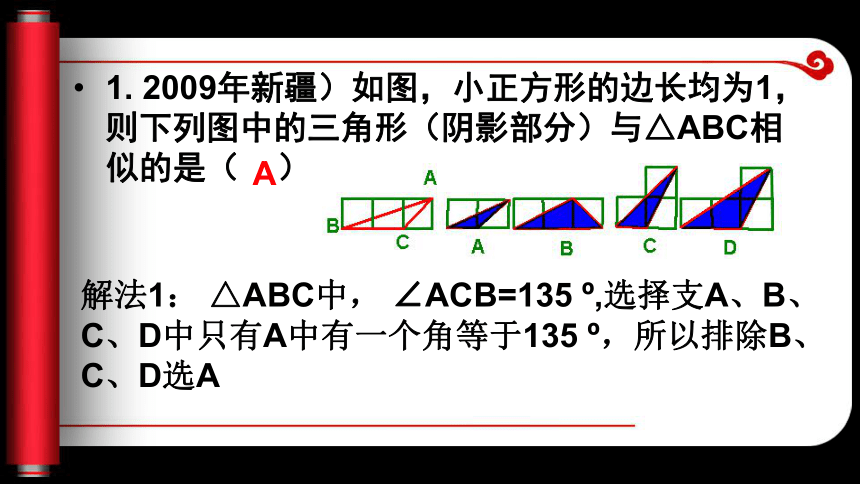
C1. 2009年新疆）如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（ ）
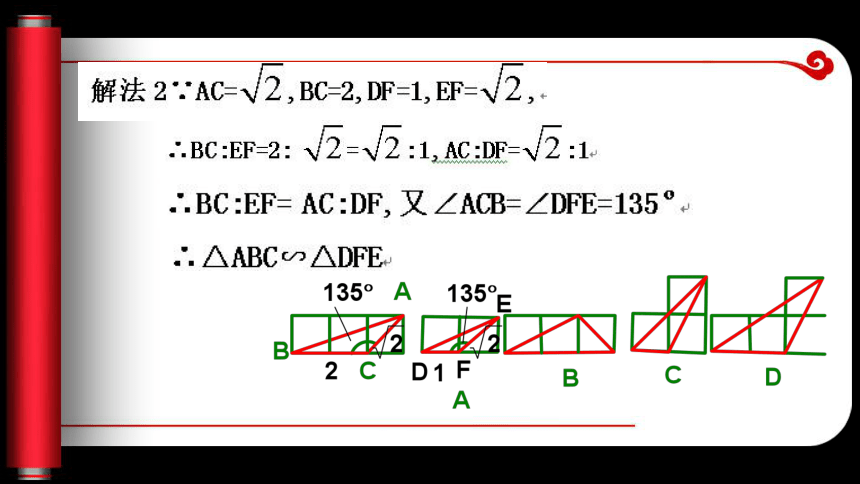
A解法1： △ABC中， ∠ACB=135 o,选择支A、B、C、D中只有A中有一个角等于135 o，所以排除B、C、D选A主题二、相似三角形的性质的应用例2. .若△ABC∽△A′B′C′,AB=3,A′B′=4.5,且S△ABC+S△A′B′C′=78,求△A′B′C′的面积。
解:设△ABC的面积为x,则△A′B′C′的面积为78-x,答：△A′B′C′的面积为36 变式练习解：∵∠C=90o, ∠B=60o，∴∠A=30o, ∵∠DEA=90o, ∴AD=2DE=2×1=2AC=AD+DC=2+2=4,∵∠A=∠A, ∠AED=∠ACB=90o, ∴△AED∽△ACB解：∵∠C=90o, ∠B=60o，∴∠A=30o, ∵∠DEA=90o, ∴AD=2DE=2×1=2AC=AD+DC=2+2=4,∵∠A=∠A, ∠AED=∠ACB=90o, ∴△AED∽△ACB例3 、（2010 山东省德州）如图，小明在A时测得某树的影长为2m，B时又测得该树的影长为8m，若两次日照的光线互相垂直，则树的高度为_____m. 主题三、相似三角形性质和判定的实际运用解：如图，已知Rt△DEF中，FG⊥DE于G。DG=2m，
GE=8m。∵∠DFG+∠GFE=90o,∠E+∠GFE=90o ∴∠DFG=∠E, 又∵∠FGD=∠FGE=90o， ∴△FGD∽△EGF, ∴DG:FG=FG:GE ，FG2=DG·GE=2×8=16,
∴FG=4(m)变式练习（2010江苏泰州，）一个铝质三角形框架三条边长分别为24cm、30cm、36cm，要做一个与它相似的铝质三角形框架，现有长为27cm、45cm的两根铝材，要求以其中的一根为一边，从另一根上截下两段（允许有余料）作为另外两边．截法有（ ）
A.0种 B. 1种 C. 2种 D. 3种
1（2009年甘肃白银）如图3，小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点．此时，竹竿与这一点相距8m、与旗杆相距22m，则旗杆的高为（　　）A．12m B.10m C．8m D．7mA2、（2010四川宜宾）如图，在Rt△ABC中，∠ACB=90°，∠A=30°，CD⊥AB于点D．则△BCD与△ABC的周长之比为（ ）A． 1:2 B． 1:3 C． 1:4 D． 1:5A3、（2010安徽芜湖）如图，光源P在横杆AB的正上方，AB在灯光下的影子为CD，AB∥CD，AB＝2m，CD＝6m，点P到CD的距离是2.7m，则AB与CD间的距离是__________m．1.84、如图，CD是Rt△ABC斜边上的高，图中相似的三角形有（ ）
A 0对 B 1对 C 2对 D 3对
D 平时要多注意培养观察能力，善于发现图中的相似三角形，并利用相似三角形得出角的相等关系，和线段的比例关系。
小结作业
P 80 ，9---11