2..3绝对值与相反数（2）

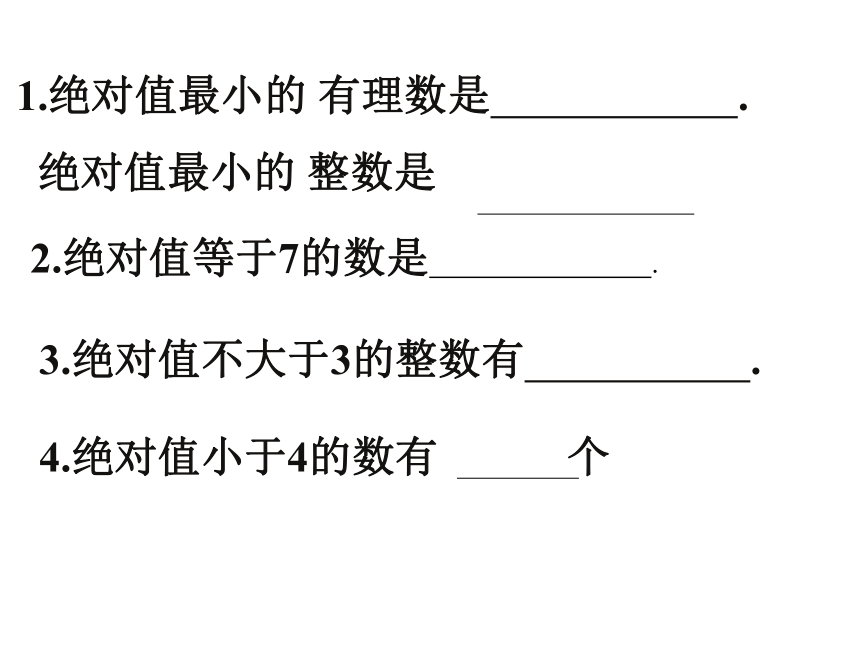
课件22张PPT。 2.3 相反数 数轴上表示一个数的点与原点的距离，叫做这个数的绝对值。复习回顾： 绝对值的定义是什么？1.绝对值最小的 有理数是 .
绝对值最小的 整数是 2.绝对值等于7的数是 .
3.绝对值不大于3的整数有 .4.绝对值小于4的数有 个 4.设a为最小的正整数，b是最大的负整数，c是绝对值最小的数，则a+b+c= ( )
A、1 B、0
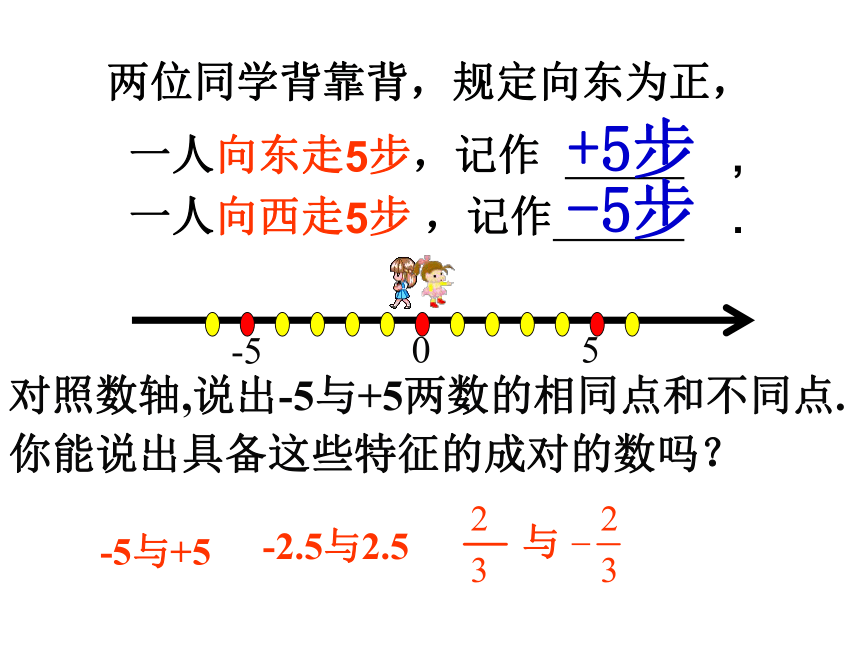
C、1或0 D、2或0一人向东走5步，记作 ,
一人向西走5步 ，记作 . 05-5+5步 -5步 对照数轴,说出-5与+5两数的相同点和不同点.-5与+5与-2.5与2.5你能说出具备这些特征的成对的数吗？两位同学背靠背，规定向东为正，规定：0的相反数是0 ⑴符号不同，绝对值相等的两个数叫做互为相反数。其中一个数叫做另一个数的相反数。注：相反数是成对出现的。1.相反数的定义：⑵只有符号不同的两个数叫做互为相反数。具备什么样特点的两个数才互为相反数呢？ 请一位同学随便报一个数，然后点名叫另一位同学说出它的相反数。总结：a的相反数是-a例1:求3、-4.5、 的相反数。解： 3的相反数是 -3 ；
- 4.5的相反数是 4； 的相反数是 -练习：p23 练一练思考：正数的相反数是什么数？
负数的相反数是什么数？
零的相反数是什么数？
什么数的相反数等于它本身？
a的相反数是什么？
a-b的相反数是什么？正数的相反数是负数；
负数的相反数是正数；
0的相反数是0；
0的相反数等于它本身;
a的相反数是-a.
a-b的相反数是b-a 相反数的表示方法 我们通常在一个数的前面加一个“-”号表示这个数的相反数。因此 –a 的相反数是 -（-a），另一方面，-a的相反数是a，所以-(-a)=a。-5的相反数表示为 +6的相反数表示为0的相反数表示为-5( )--( )+6=5=-6=0
⑴ -（+5） ⑵ +（-3）
⑶ +（+2） ⑷ -（-6）例2：说出下列各数的意义，并化简：解：-（+5）表示+5的相反数，+（-3）表示-3的本身，+（+2）表示+2的本身，-（-6）表示-6的相反数，-（+5）=-5+（-3）=-3+（+2）=+2-（-6）=+6 练习：利用相反数的意义化简：
⑴－ [－ (+5.3)]
⑵－[－(－3.2)]
⑶－ {－ [－( －8)]}
它们的符号变化有什么规律？把一个数的多重符号化成单一符号时，若该数前面有奇数个“－”号，则化简结果是负数，若该数前面有偶数个“－”号,则化简结果是正数。1.下列说法正确的是（ ）
A．正数与负数互为相反数
B．符号不同的两个数互为相反数
C．数轴上原点两旁的两个点所表示的数是互为相反数
D．任何一个有理数都有它的相反数
2.下列说法：
①有理数的绝对值一定是正数；
②一个数的绝对值的相反数一定是负数；
③互为相反数的两个数,必然一个是正数,一个是负数；
④互为相反数的绝对值相等；
⑤a的相反数是-a；
其中正确的个数有 （ ）
A.0个 B.1个 C.2个 D.3个3.填空：
① -1相反数是_____；-2是____的相反数；____与-（-6）互为相反数．
② 绝对值等于5的数有___个，它们____．
③ -1的相反数的绝对值为________，
-1的绝对值的相反数为_________．
4.一个数的相反数是非正数,这个数一定是( )
A 非正数 B. 非负数 C非零的数 D负数.5. 下列各对数中互为相反数是?（ ）
A．-（+3）和+（-3）???
B．-（-3）和+（-3）
C．-（+3）和 -3??????
D．+（-3）和 -36.在-3的绝对值与2的相反数之间的整数是 .
7. 下列说法:
① 如果a=－13,那么－a = 13,
② 如果a是非负数,那么－a是正数,
③ 如果a是负数,那么︳a ︴+1是正数,
其中正确的是 （ ）
A ①③ B①②　 C②③　D①②③ 8. ⑴如果a的相反数是-3，则a=
⑵如果a-5的相反数是-3，则a=
⑶若-（-3x）=12,则x=
9.数轴上，若A、B表示互为相反数，且 A在B的右侧，如果这两点的距离为8，则这两点所表示的数分别是____和___ ． 0ab10.已知a,b有理数在数轴上表示如图
⑴比较a,b的大小,
⑵比较︱ a︱ ,︱ b︱的大小,
⑶比较 a, b, - a, - b的大小.思考：(1)如果a,b互为相反数, 则
a+b= ( )
a÷b= ( ) (b ≠0 )
(2)如果a+b=0,则 a,b的关系是为：?小结回头一看，我想说…相反数成对出现。说说你对相反数的认识。只有符号不同的两个数才互为相反数。 数轴上表示相反数的两个对应点，分别位于原点两侧，它们到原点距离相等。