23.2.1中心对称

课件18张PPT。欢迎各位家长、老师
莅临指导！23.2.1 中心对称学习目标1.理解中心对称的概念，知道什么是对称中心、对称点。2. 探索中心对称图形的性质.3.会作一个已知图形的中心对称图形及会找出两个中心对称图形的对称中心。自学指导1. 请同学们认真看课本P68“观察”的内容,你发现了什么？与同桌交流一下。自学竞赛开始啦！2.认真阅读“观察”下的文字，了解中心对称的概念,以及对称中心、对称点。待会我们比比谁能正确的做出类似的习题。 180° ⒉.下列图形是中心对称图形的是( ) (是中心对称图形的请指出对称中心)
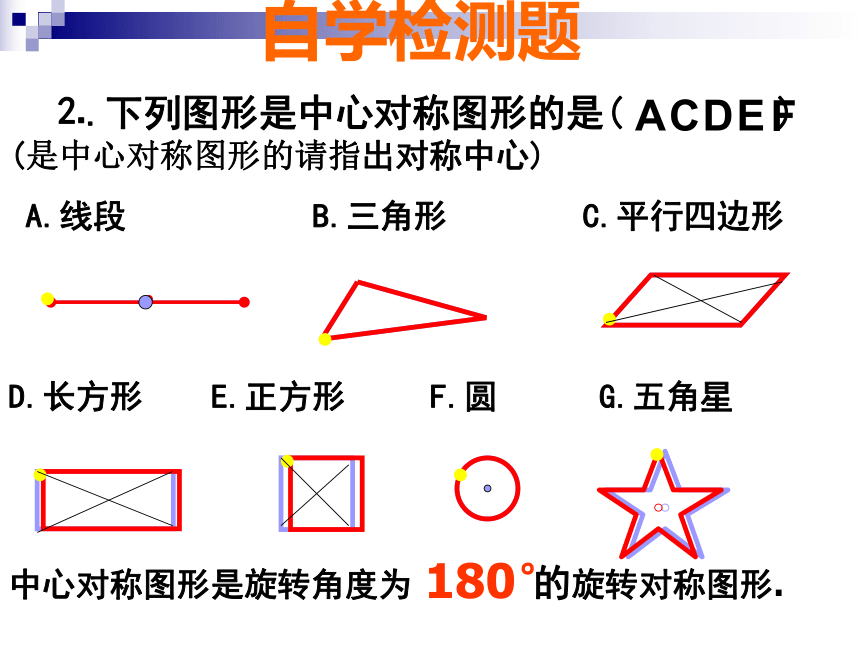
A.线段 B.三角形 C.平行四边形

D.长方形 E.正方形 F.圆 G.五角星


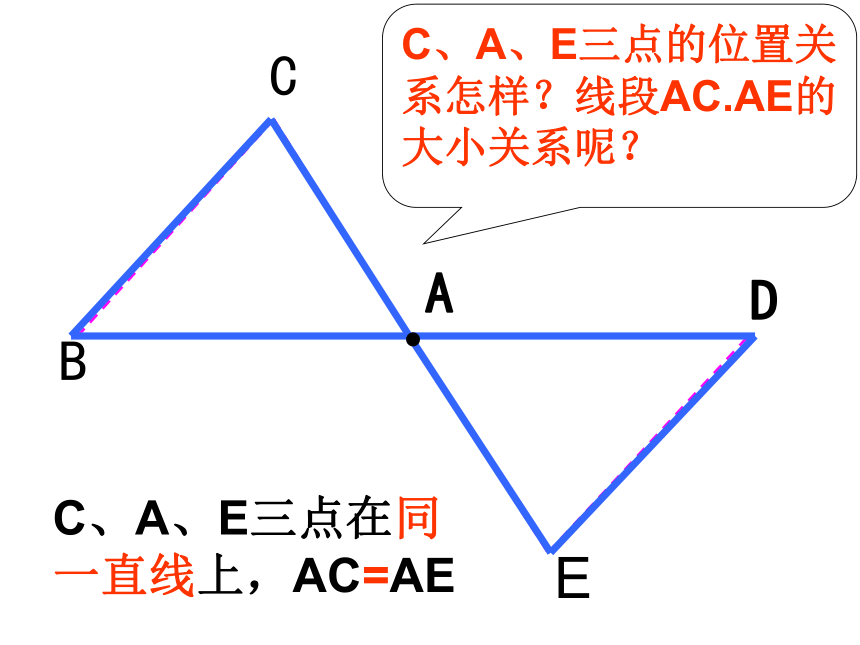
中心对称图形是旋转角度为 的旋转对称图形.自学检测题180°ACDFEABCEDC、A、E三点的位置关系怎样？线段AC.AE的大小关系呢？C、A、E三点在同一直线上，AC=AE 在下图中，ΔA’B’C’与ABC关于点O是成中心对称的，你能从图中找到哪些等量关系？OC’B’A’ACB(1)OA=OA′、OB=OB′、 OC=OC′（2）△ABC≌△A′B′C′归纳：
（1）在成中心对称的两个图形中,连接对称点的线段都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.（2）关于中心对称的两个图形是全等图形。
AA′B′BO 2、线段的中心对称线段的作法AOA′1、点的中心对称点的作法灵活运用，体会内涵
以点O为对称中心,作出点A的对称点A′;
以点O为对称中心,作出线段AB的对称线段点A′B′
点A′即为所求的点例1 (2)如图23.2-5,选择点O为对称中心,画出与
△ABC关于点O对称的△A′B′C′.解:A′C′B′△A′B′C′即为所求的三角形。
练习： 任意作四边形ABCD和任意确定一点O，画四边形A′B′C′D′，使它与已知四边形关于这一点对称。ABA’C’B’D’DOC四边形A１B１C１D１即为所求的图形。 如图，已知△ABC与△A’B’C’中心对称，求出它们的对称中心O。应用解法一：根据观察，B、B’应是对应点，连结BB’，用刻度尺找出BB’的中点O，则点O即为所求（如图）OO解法二：根据观察，B、B’及C、C’应是两组对应点，连结BB’、CC’，BB’、CC’相交于点O，则点O即为所求（如图）。
画一个与已知四边形ABCD中心对称图形。
（1）以顶点A为对称中心；
（2）以BC边的中点为对称中心。提高练习EFGMN作业:
P74. 1谢谢！
再见！