函数的表示法
图片预览







文档简介
课件23张PPT。1.2.2函数的表示法学习过程一、复习函数的三种表示方法初中学习过哪几种函数的表示法?解析法、图象法、列表法问题实例(1)中的函数是用解析法表示的,简明表示了h与t之间的关系,也可用图象法、列表法表示,但列表法不能全面表示变量间的关系。课本1.2.1节的三个实例分别用了哪些表示方法?能否用其它的表示方法?其各自的优点是什么?实例(2)中的函数是用图象法表示的,直观形象地表明了函数的变化趋势,此函数的解析式不易得到,列表法也不能形象地表示其变化趋势。实例(3)中的函数是用列表法表示的,可直接看出恩格尔系数随年数变化的情况,也可用图象法表示,但解析式不明确。问题三种表示方法的优点解析法图象法列表法①函数关系清楚、精确②容易从自变量的值求出其对应的函数值③便于研究函数的性质。解析法是中学研究函数的主要表达方法。能形象直观的表示出函数的变化趋势,是今后利用数形结合思想解题的基础。不必通过计算就知道当自变量取某些值时函数的对应值,当自变量的值的个数较少时使用,列表法在实际生产和生活中有广泛的应用。解:这个函数的定义域是数集{1,2,3,4,5}
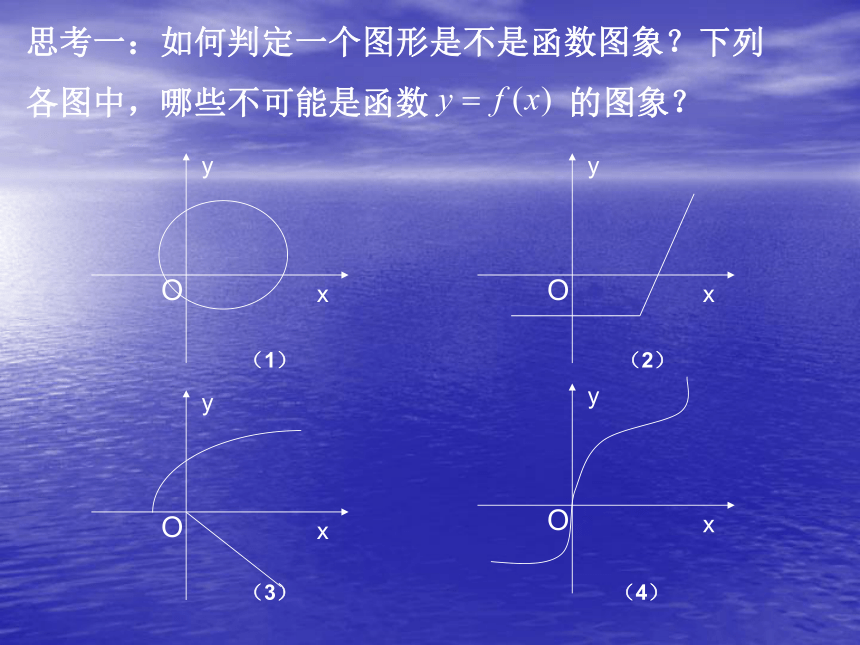
用解析法可将函数y=f(x)表示为用列表法可将函数表示为【例3 】某种笔记本的单价是5元,买x 个笔记本需要y元。试用函数的三种表示法表示函数二、学习例3,掌握用三种方法表示函数用图象法可将函数表示为下图.....问题(1)用解析法表示函数是否一定要写出自变量的取值范围?(2)用描点法画函数图象的一般步骤是什么?本题中的图象为什么不是一条直线? 函数的定义域的函数存在的前提,再写函数解析式的时候,一定要写出函数的定义域。列表、描点、连线(视其定义域决定是否连线)函数的图象既可以是连续的曲线,也可以是直线、折线、离散的点等。思考一:如何判定一个图形是不是函数图象?下列
各图中,哪些不可能是函数 的图象?(1) (2)
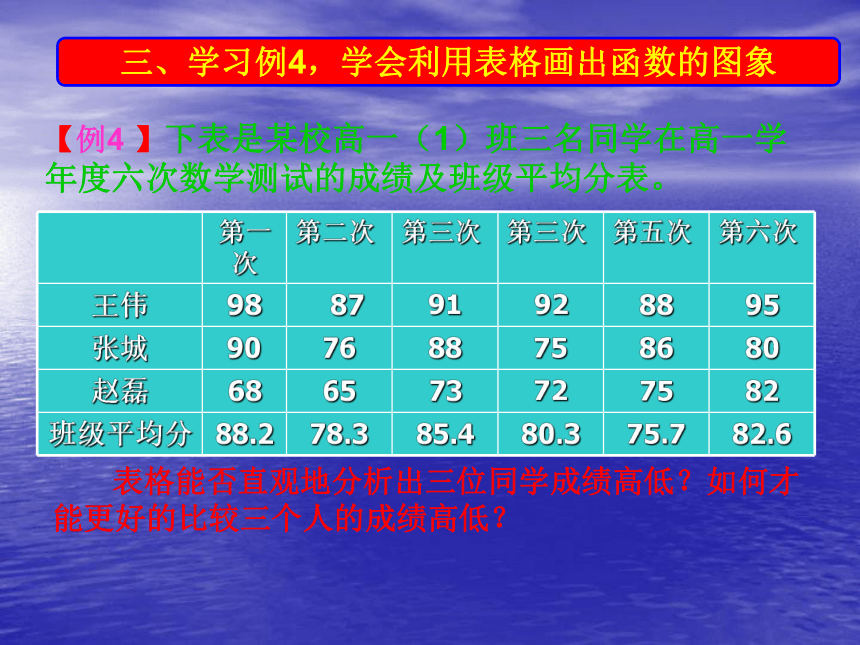
(3) (4)【例4 】下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表。三、学习例4,学会利用表格画出函数的图象 表格能否直观地分析出三位同学成绩高低?如何才能更好的比较三个人的成绩高低?......▲▲
▲
▲
▲
▲
■■■■■??????王伟■张城班平均分赵磊解:将“成绩”与“测试时间”之间的关系用函数图象表示出来。可以看出:王伟同学学习情况稳定且成绩优秀;张城同学的成绩在班级平均水平上下波动,且波动幅度较大;赵磊同学的成绩低于班级平均水平,但成绩在稳步提高。例5、画出函数 的图象。解:由绝对值的概念,我们有所以,函数 的图象如下图所示 练习: 1.画出下列函数图像,并求其值域。
例6、某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算)。
如果某条线路的总里程为20公里,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象。解:设票价为 ,里程为 ,依题意得:分段函数 所谓“分段函数”,习惯上指在定义域的不同部
分,有不同的对应法则的函数,对它应有以下两点
基本认识:
(1)分段函数是一个函数,不要把它误认为是几
个函数;
(2)分段函数的定义域是各段定义域的并集,值
域是各段值域的并集。例7 练习:1.学案P15第5题 2.学案P15第6题映射一般地,我们有:
设A、B是非空集合,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数y和它对应,那么称f:A→B为从集合A到集合B的一个映射。(mapping)。例7、以下给出的对应是不是从集合A到集合B的映射?
(1)集合A={P|P是数轴上的点},集合B=R,对应关系f:数
轴上的点与它所代表的实数对应;
(2)集合A={P|P是平面直角坐标系中的点},
集合B= ,对应关系f:平面直角坐标
系中的点与它的坐标对应;
(3)集合A={x|x是三角形},集合B={x|x是圆},对应关系f :
每一个三角形都对应它的内切圆;
(4)集合A={x|x是新华中学的班级},集合B={x|x是新华中
学的学生},对应关系f :每一个班级都对应班里的学生。课堂练习布置作业:
课本习题1.2P24,A组
5题上作业
做学案P16检测题
用解析法可将函数y=f(x)表示为用列表法可将函数表示为【例3 】某种笔记本的单价是5元,买x 个笔记本需要y元。试用函数的三种表示法表示函数二、学习例3,掌握用三种方法表示函数用图象法可将函数表示为下图.....问题(1)用解析法表示函数是否一定要写出自变量的取值范围?(2)用描点法画函数图象的一般步骤是什么?本题中的图象为什么不是一条直线? 函数的定义域的函数存在的前提,再写函数解析式的时候,一定要写出函数的定义域。列表、描点、连线(视其定义域决定是否连线)函数的图象既可以是连续的曲线,也可以是直线、折线、离散的点等。思考一:如何判定一个图形是不是函数图象?下列
各图中,哪些不可能是函数 的图象?(1) (2)
(3) (4)【例4 】下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表。三、学习例4,学会利用表格画出函数的图象 表格能否直观地分析出三位同学成绩高低?如何才能更好的比较三个人的成绩高低?......▲▲
▲
▲
▲
▲
■■■■■??????王伟■张城班平均分赵磊解:将“成绩”与“测试时间”之间的关系用函数图象表示出来。可以看出:王伟同学学习情况稳定且成绩优秀;张城同学的成绩在班级平均水平上下波动,且波动幅度较大;赵磊同学的成绩低于班级平均水平,但成绩在稳步提高。例5、画出函数 的图象。解:由绝对值的概念,我们有所以,函数 的图象如下图所示 练习: 1.画出下列函数图像,并求其值域。
例6、某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算)。
如果某条线路的总里程为20公里,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象。解:设票价为 ,里程为 ,依题意得:分段函数 所谓“分段函数”,习惯上指在定义域的不同部
分,有不同的对应法则的函数,对它应有以下两点
基本认识:
(1)分段函数是一个函数,不要把它误认为是几
个函数;
(2)分段函数的定义域是各段定义域的并集,值
域是各段值域的并集。例7 练习:1.学案P15第5题 2.学案P15第6题映射一般地,我们有:
设A、B是非空集合,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数y和它对应,那么称f:A→B为从集合A到集合B的一个映射。(mapping)。例7、以下给出的对应是不是从集合A到集合B的映射?
(1)集合A={P|P是数轴上的点},集合B=R,对应关系f:数
轴上的点与它所代表的实数对应;
(2)集合A={P|P是平面直角坐标系中的点},
集合B= ,对应关系f:平面直角坐标
系中的点与它的坐标对应;
(3)集合A={x|x是三角形},集合B={x|x是圆},对应关系f :
每一个三角形都对应它的内切圆;
(4)集合A={x|x是新华中学的班级},集合B={x|x是新华中
学的学生},对应关系f :每一个班级都对应班里的学生。课堂练习布置作业:
课本习题1.2P24,A组
5题上作业
做学案P16检测题
